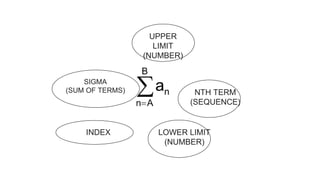
This document introduces arithmetic sequences and series. It defines an arithmetic sequence as a sequence where the difference between consecutive terms is constant. The nth term of an arithmetic sequence can be written as a formula of a, the first term, and d, the common difference. An arithmetic series is the sum of terms in an arithmetic sequence, which can be calculated using the sigma notation and the formula for the sum of an arithmetic sequence. Examples are provided to illustrate finding terms and sums of arithmetic sequences and series.

1. Arithmetic Sequences and
series

2. Introduce Sequence

3. Introduce Series

4. Contents

5. Sequences
9, 16, 25, 36, 49, …
is a sequence of square numbers starting with 9.
A sequence can be infinite, as shown by the … at the end of the
sequence shown above, or it can be finite. For example:
3, 6, 12, 24, 48, 96
is a finite sequence containing six terms.

6. The formula for the n
th term
For example, the formula for the n
th term of a sequence is given by un = 4n – 5.
The first five terms in the sequence are: –1, 3, 7, 11 and 15.

7. The formula for the n
th term

8. Recurrence relations
This sequence can also be defined by a recurrence relation.
To define a sequence using a recurrence relation we need
the value of the first term and an expression relating each
term to a previous term.
For the sequence –1, 3, 7, 11, 15, …, each term can be found
by adding 4 to the previous term.
We can write:

9. Recurrence relations
A recurrence relation together with the first term of a sequence is called an
inductive definition.
So the inductive definition for the sequence –1, 3, 7, 11, 15, … is u1 = –1, un+1 = un +
4.
So the first five terms in the sequence are 3, 7, 15, 31 and 63

10. Using an inductive definition

11. Arithmetic sequences
In an arithmetic sequence (or arithmetic progression) the difference
between any two consecutive terms is always the same. This is called the
common difference.
For example, the sequence: 8, 11, 14, 17, 20, …
is an arithmetic sequence with 3 as the common difference.
We could write this sequence as:

12. Arithmetic sequences
If we call the first term of an arithmetic sequence a and the common
difference d we can write a general arithmetic sequence as:

13. Arithmetic sequences Example
This is an arithmetic sequence with first term a = 10 and common
difference d = –3 -> u2-u1 = u3-u2 =7-10 = -3 .
The nth term is given by a + (n – 1)d so:
Let’s check this formula for the first few terms in the sequence:

14. Arithmetic sequences Example 2
This is an arithmetic sequence with first term a = –7 and common difference d = 6.
The n
th term is given by a + (n – 1)d so:
We can find the value of n for the last term by solving:
So, there are 14 terms in the sequence.

15. Arithmetic sequences Example 3

16. Try … Arithmetic sequences
The first five terms of an arithmetic sequence are:
−20,−17,−14,−11,−8
a=-20, d=3 -> d = -17 -(-20)=3
n
th term = -20+3(n-1)
n
th term = -20+3n-3= 3n-23
Find an expression for the n
th term of the sequence.

17. Try … Arithmetic sequences
Here is a picture of four models. Some of the cubes are hidden behind other cubes.
Model one consists of one cube. Model two consists of four cubes and so on.
(a) How many cubes are in the third model?
(b) How many cubes are in the fourth model?
(c) If a fifth model were built, how many cubes would it take?
(d) Find an expression for the number of cubes used in the nth model.

18. Answers :
a) 9
b) 16
c) 25
d) nth = n^2

19. Try … Arithmetic sequences
Determine the twelfth term of arithmetic sequence whose first term is
-6 and whose difference is 4.
Nth term = a + ( n-1) d
12th term = -6 + (12-1) 4
-6 + 11 x 4
-6 + 44
38

20. Try … Arithmetic sequences
The 4th term of an arithmetic sequences is 110 and the 9th term of
arithmetic sequences is 150. Find the 30th term of that arithmetic
sequence.
Answer : 9-4 = 5 150-110 = 40 40/5=8
8x4= 32 110-32=78 (30x8)+78=318
4th = a + 3d = 110 9th = a + 8d = 150
30 th = 86 + 29(8) = 318
A + 3d = 110
A + 8d = 150 -
------------------------
5d=40
D = 8 a = 86

21. Months Cost ($)
1 75,000
2 90,000
3 105,000
4 120,000
The table shows typical costs for a construction company to rent a crane for
one, two, three, or four months. Assuming that the arithmetic sequence
continues, how much would it cost to rent the crane for twelve months?
Try … Arithmetic sequences

22. 75,000
12
NA
15,000
a12 = 75,000 + (12 - 1)(15,000)
a12 = 75,000 + (11)(15,000)
a12 = 75,000+165,000
a12 = $240,000
Answer :

23. Arithmetic Series
Arithmetic Series: An indicated sum of terms in an
arithmetic sequence.
Example:
Arithmetic Sequence VS Arithmetic Series
3, 5, 7, 9, 11, 13 3 + 5 + 7
+ 9 + 11 + 13

24. Vocabulary of Sequences (Universal)
Recall

25. -19
63
??
Sn
6
353
Find the sum of the first 63 terms of the arithmetic sequence -19, -13, -7,…
a63 = 353

26. Find the first 3 terms for an arithmetic series in which a1 = 9, an = 105, Sn =741.
9
??
105
741
??
13
9, 17, 25

27. A radio station considered giving away $4000 every day in the month of August for a
total of $124,000. Instead, they decided to increase the amount given away every day
while still giving away the same total amount. If they want to increase the amount by
$100 each day, how much should they give away the first day?
a1
31 days
??
$124,000
$100/day

28. Sigma Notation ( )
Used to express a series or its sum in abbreviated form.

29. UPPER
LIMIT
(NUMBER)
LOWER LIMIT
(NUMBER)
SIGMA
(SUM OF TERMS) NTH TERM
(SEQUENCE)
INDEX

30. If the sequence is arithmetic (has a common difference) you can use the Sn formula
1+2=3
4
4+2=6
??
NA

31. Is the sequence arithmetic?
10 + 17 + 26 + 37
No, there is no common difference
Thus you cannot use the Sn formula.
= 90
= 2.71828

32. Rewrite using sigma notation: 3 + 6 + 9 + 12
Arithmetic, d= 3