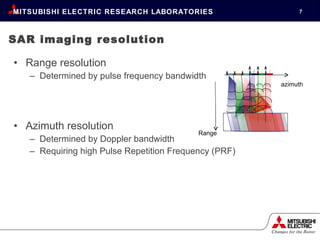
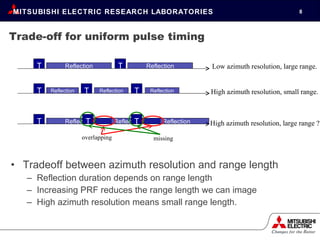
This document proposes using random pulse timing in synthetic aperture radar (SAR) imaging to achieve high azimuth resolution while maintaining full ground range coverage. It describes how compressive sensing allows for undersampling by mixing missing data through randomization. An iterative reconstruction algorithm is used to incorporate the sparsity prior and reconstruct high-resolution SAR images from randomly sampled radar echo data. Simulation results using synthetic data demonstrate the approach can produce images with improved azimuth resolution compared to uniform pulse timing schemes.

1. High resolution SAR imaging using random pulse timing Dehong Liu IGARSS’ 2011 Vancouver, CANADA Joint work with Petros Boufounos.

3. Overview of SAR

4. Synthetic Aperture Radar (SAR) Ground Range v azimuth azimuth Reflection duration depends on range length.

5. Strip-map SAR: uniform pulsing Ground azimuth Range azimuth v

10. Compressive sensing and random pulse timing

14. Random pulse timing Randomized pulsing interval azimuth range Randomized timing mixes missing data

15. Iterative reconstruction algorithm

16. Iterative reconstruction algorithm Note: Fast computation of  and  H always speeds up the algorithm.

17. Efficient computation  Azimuth FFT Chirp Scaling (differential RCMC) Range FFT Bulk RCMC, RC, SRC Range IFFT F r F a S -1 F r -1 P a H F a -1 Azimuth Compression/ Phase Correction Azimuth IFFT Chirp Scaling Algorithm Computation of  follows reverse path Computation as efficient as CSA y P r H B -1 R -1

18. Imaging results with synthetic data

20. Radar Image Radar Raw Data Ground Classic Pulsing low PRF Random Pulsing high PRF + missing data Image with low azimuth resolution Image with high azimuth resolution Radar data acquisition Forward process Standard Algorithm Iterative Algorithm Simulated Ground Reflectivity (high-resolution)

21. Zoom-in imaging results True Ground Reflectivity Uniform pulsing, Small PRF, Small Doppler Bandwidth Random pulsing, High PRF, Large Doppler Bandwidth

22. Zoom-in imaging results True Ground Reflectivity Uniform pulsing, Small PRF, Small Doppler Bandwidth Random pulsing, High PRF, Large Doppler Bandwidth

23. Conclusion and future work