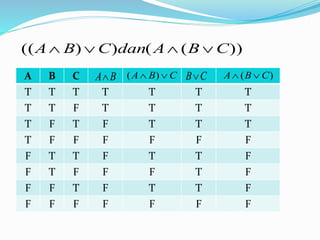
Dokumen ini membahas ekuivalensi logis dalam logika matematika, termasuk tautologi, kontradiksi, dan contingent. Contoh-contoh diberikan untuk membuktikan ekivalensi logis menggunakan tabel kebenaran, serta penekanan pada pentingnya tanda kurung dalam ekspresi logika. Terdapat pembahasan juga mengenai sifat komutatif dan asosiatif dalam logika.

1. Logika Matematika
Pertemuan ke - 4

2. Ekuivalen Logis
 Pada tautologi dan juga kontradiksi, dapat dipastikan
bahwa jika dua buah ekspresi logika adalah tautologi,
maka kedua ekspresi logika tersebut Ekivalen secara
logis, demikian juga jika keduanya kontradiksi.
 Persoalannya ada pada contingent, karena memiliki
semua nilai T dan F. Tetapi jika urutan T dan F atau
sebaliknya pada tabel tetap pada urutan yang sama,
maka tetap disebut Ekivalen secara Logika

3. Contoh 1
(1). Dewi sangat cantik dan peramah.
(2). Dewi Peramah dan sangat cantik.

4. Penyelesaian
 Dalam Bentuk Ekspresi Logika
A = Dewi sangat cantik.
B = Dewi Peramah.
 Maka Ekspresi Logika tersebut adalah:
AB
BA


).2(
).1(

5.  Jika dikatakan kedua buah Ekspresi Logika tersebut
Ekivalen secara logis, maka dapat ditulis:
 Ekivalensi logis dari kedua ekspresi logika tersebut
dapat dibuktikan dengan Tabel Kebenaran berikut ini:
ABBA 
A B
T T T T
T F F F
F T F F
F F F F
BA AB

6. Contoh 2
(1). Badru tidak pandai, atau dia tidak jujur.
(2). Adalah tidak benar Jika Badru pandai dan jujur.

7. Penyelesaian
 Dalam Bentuk Ekspresi Logika
A = Badru pandai.
B = Badru Jujur.
 Maka Ekspresi Logika tersebut adalah:
)().2(
).1(
BA
BA



8.  Jika dikatakan kedua buah Ekspresi Logika tersebut
Ekivalen secara logis, maka dapat ditulis:
 Ekivalensi logis dari kedua ekspresi logika tersebut
dapat dibuktikan dengan Tabel Kebenaran berikut ini:
)()( BABA 
A B
T T F F T F F
T F F T F T T
F T T F F T T
F F T T F T T
A B BA BA  )( BA

9. Komutatif
 Jadi
 Demikian juga dengan V, maka
 Demikian juga dengan V, maka
 Akan tetapi , perangkai tidak
memiliki sipat komutatif .
)()( ABBA 
)()( ABBA 
)()( ABBA 
)(Implikasi

10.  Pembuktian dengan menggunakan tabel kebenaran:
A B
T T T T
T F F T
F T T F
F F T T
BA AB 

11. Asosiatif
 Penempatan tanda kurung biasa pada suatu ekspresi
logika memegang peranan penting, karena tanda
kurung berarti meminta proses dikerjakan terlebih
dahulu pada tanda kurung terdalam.
 Contoh :
))(())(( CBAdanCBA 

12.  Maka Tabel kebenarannya adalah sebagai berikut:
 Jadi :
A B C
T T T T T T T
T T F T F F F
T F T F F F F
T F F F F F F
F T T F F T F
F
F
T
F
F
T
F
F
F
F
F
F
F
F
F F F F F F F
BA CBA  )( CB  )( CBA 
))(())(( CBACBA 

13.  Akan tetapi jika perangkainya berbeda pada satu
ekspresi logika, akan menghasilkan nilai kebenaran
yang berbeda.
 Contoh. 3
))(())(( CBAdanCBA 

14. A B C
T T T T T T T
T T F T T T T
T F T F T T T
T F F F F F F
F T T F T T F
F T F F F T F
F F T F T T F
F F F F F F F
))(())(( CBAdanCBA 
BA CBA  )( CB )( CBA 

15. Penghapusan tanda kurung
 Contoh:
 Contoh:
CABA
CABA


)(
)()(
CBAA
CBAA
CABA



))((
)(
)(

16. Contoh.4
(1). Jika Badru tidak sekolah, maka Badru tidak akan
pandai.
(2). Jika Badru pandai, maka Badru pasti sekolah

17. Penyelesaian
 Dalam Bentuk Ekspresi Logika
A = Badru sekolah.
B = Badru Pandai.
 Maka Ekspresi Logika tersebut adalah:
AB
BA


).2(
).1(

18.  Pembuktian Ekuivalensi dengan Tabel Kebenaran
berikut ini:
 Jadi, terbukti bahwa:
)()( ABBA 
A B
T T F F T T
T F F T T T
F T T F F F
F F T T T T
A B AB BA 

19. Contoh.5
(1).
(2).
BA 
)()( ABBA 

20.  Pembuktian Ekuivalensi dengan Tabel Kebenaran
berikut ini:
 Jadi, terbukti bahwa:
)()()( ABBABA 
A B
T T T T T T
T F F F T F
F T F T F F
F F T T T T
BA  BA )()( ABBA AB

21.  Dalam Tautologi, Nilai kebenaran dapat diganti
seperti berikut:
True (T) = 1
False (F) = 0
Tabel kebenaran :
A 1 0
T T F T F
F T F F F
1A 0A

22. Tugas
 Buktikan bahwa ekspresi-ekpresi logika berikut ini
ekuivalen dengan menggunakan tabel kebenaran:
1)))(())().((7(
0)(().6(
)().5(
)()().4(
)()).(3(
1)().2(
)()().1(







ACBACBA
BBA
BABA
CBACBA
CBACBA
BAA
ABBABA