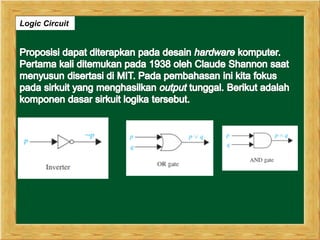
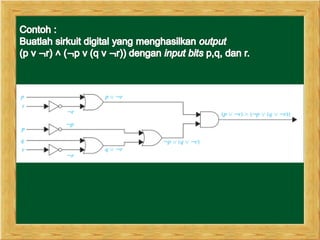
Dokumen ini membahas tentang logika dan pembuktian, termasuk proposisi, negasi, konjungsi, disjungsi, implikasi, dan biimplikasi. Juga dibahas penerapan logika dalam konteks matematika dan sains, serta pemahaman tentang kuantor universal dan eksistensial yang membantu dalam menyatakan nilai kebenaran. Konsep ekuivalensi proposisi dan argumen satisfiable serta unsatisfiable juga dijelaskan untuk memperdalam pemahaman mengenai logika.

1. LOGIKA DAN PEMBUKTIAN-PEMBUKTIAN
1.1 Logika Proposisi
1.2 Penerapan Logika Proposisi
1.3 Ekuivalensi Proposisi
1.4 Predikat dan Kuantor
1.5 Kuantor Bersusun
Isnaendi Ruhyana
90115005
Magister Pengajaran Matematika

2. 1. Logika Proposisi
Proposisi adalah kalimat yang memuat fakta
yang bernilai benar atau salah namun tidak
keduanya
Apa itu proposisi?

3. Berikut ini adalah contoh beberapa proposisi. Manakah proposisi
yang bernilai benar?
1. Jakarta adalah ibukota negara Indonesia
2. Bandung berada di provinsi Jawa Tengah
3. 1+1=2
4. 2+2=3
Proposisi 1 dan 3 bernilai benar sedangkan proposisi 2 dan 4
bernilai salah

4. Berikut ini adalah contoh beberapa kalimat yang bukan proposisi:
1. Pukul berapa sekarang?
2. Bacalah teks berikut dengan saksama!
3. x+1=2
4. x+y=z
Mengapa kalimat-kalimat tersebut bukan termasuk proposisi?
Kalimat 1 dan 2 bukan kalimat yang memuat fakta
Kalimat 3 dan 4 tidak dapat ditentukan benar atau salah

5. • Definisi 1
Misalkan p sebuah proposisi. Negasi p (dilambangkan dengan
¬p) adalah pernyataan “ tidak benar bahwa p”.
¬p dibaca bukan p
Nilai kebenaran ¬p bertentangan dengan nilai kebenaran p
Contoh :
Smartphone Vandana mempunyai memori ≥ 32 GB
Negasinya :
• Tidak benar bahwa smartphone Vandana
mempunyai memori paling sedikit 32 GB
• Smartphone Vandana tidak mempunyai memori
paling sedikit 32 GB
• Smartphone Vandana mempunyai memori < 32
GB
Nilai
Kebenaran
p dan ¬p
p ¬p
B S
S B
NEGASI

6. • Definisi 2
Misalkan p dan q proposisi. Konjungsi dari p dan q
(dilambangkan dengan p ᴧ q) bernilai benar apabila p dan q
keduanya benar.
Nilai Kebenaran
Konjungsi p dan q
p q p ᴧ q
B B B
B S S
S B S
S S S
Contoh :
Calon mahasiswa Pascasarjana ITB
dinyatakan diterima apabila nilai TPA ≥ 475
dan TOEFL ≥ 475
KONJUNGSI

7. DILARANG MEMBAWA
MAKANAN DAN MINUMAN
KE DALAM RUANGAN INI

8. • Definisi 3
Misalkan p dan q proposisi. Disjungsi p dan q (dilambangkan
dengan p v q) adalah proposisi p atau q. Nilai kebenaran
disjungsi p v q bernilai salah apabila p dan q keduanya salah.
Contoh :
Mahasiswa di ruangan ini gemar membaca atau
menulis.
Nilai Kebenaran
Disjungsi p dan q
p q p v q
B B B
B S B
S B B
S S S
DISJUNGSI

9. • Inclusive or dan exclusive or
• Contoh exclusive or :
Jenis kelamin manusia terdiri dari laki-laki atau perempuan.
Nilai Kebenaran
inclusive or
p q p v q
B B B
B S B
S B B
S S S
Nilai Kebenaran
exclusive or
p q 𝑝 ⊕ 𝑞
B B S
B S B
S B B
S S S

10. • Definisi 5
Misalkan p dan q proposisi.
Implikasi p→q adalah proposisi jika p maka q. Implikasi p→q
bernilai salah apabila p benar dan q salah.
p disebut sebagai hipotesis (premis) sedangkan q disebut
sebagai kesimpulan (konklusi)
Nilai Kebenaran
Implikasi p dan q
p q p → q
B B B
B S S
S B B
S S B
Contoh :
Jika saya rajin belajar maka saya akan
lulus ujian.
IMPLIKASI

11. • Konvers, Invers dan kontraposisi
Implikasi
𝑝 → 𝑞
Konvers
𝑞 → 𝑝
Invers
¬𝑝 → ¬𝑞
Kontraposisi
¬𝑞 → ¬𝑝
Bernilai salah untuk
p benar dan q salah
Bernilai salah untuk
¬p salah dan ¬q benar
Bernilai salah untuk
¬p benar dan ¬q salah
Bernilai salah untuk
p salah dan q benar
Kesimpulan:
p → q ≡ ¬q → ¬p
q → p ≡ ¬p → ¬q

12. • Definisi 6
Misalkan p dan q proposisi. Argumentasi biimplikasi dari p↔q
adalah proposisi p jika dan hanya jika q. Biimplikasi bernilai
benar ketika p dan q memiliki nilai kebenaran yang sama.
Nilai Kebenaran
Biimplikasi p dan q
p q p ↔ q
B B B
B S S
S B S
S S B
Contoh : Anda dapat naik pesawat jika dan
hanya jika sudah memiliki tiket.
BIIMPLIKASI

13. Komposisi majemuk adalah gabungan beberapa proposisi yang
dihubungkan dengan operator logika (¬, ˄, ˅, →, ↔). Contoh
komposisi majemuk p˄q, pvq, p→q, p↔q.
Precedence
(tingkat prioritas)
Operator Precedence
¬ 1
˄ 2
˅ 3
→ 4
↔ 5
KOMPOSISI MAJEMUK
Contoh:
Tentukan nilai kebenaran (p v ¬q) → (p˄q)
menggunakan tabel kebenaran!
p q ¬q p v ¬q p˄q (p v ¬q) → (p˄q)
B B S B B B
B S B B S S
S B S S S B
S S B B S S

14. p q p˄q p v q p⊕q
1 1 1 1 0
1 0 0 1 1
0 1 0 1 1
0 0 0 0 0
BIT OPERATION
Nilai kebenaran dalam logika dapat diterjemahkan dalam bentuk bit sehingga
dapat diterjemahkan oleh komputer. Jika suatu proposisi benar maka bernilai
1, jika salah bernilai 0. Perhatikan tabel kebenaran berikut untuk dapat
memahami penggunaan bit oleh komputer.

15. 1.2 Penerapan Logika Proposisi
Logika banyak digunakan dalam berbagai ilmu
seperti matematika, sains komputasi.
Mengapa bahasa dalam bentuk logika banyak digunakan?
Pernyataan-pernyataan dalam matematika, sains dan bahasa
umum sering tidak tepat atau ambigu (bermakna ganda). Oleh
karena itu perlu digunakan bahasa logika untuk
menghilangkan ambiguitas tersebut.

16. Spesifikasi Sistem

17. Teka-teki Logika

18. Logic Circuit

20. 1.3 Ekuivalensi Proposisi
• Definisi 1
Proposisi majemuk yang selalu benar apapun nilai kebenaran
variabelnya disebut tautologi. Proposisi majemuk yang selalu
salah disebut kontradiksi. Proposisi majemuk yang tidak
termasuk tautologi dan kontradiksi disebut kontingensi.
p ¬p p v ¬p p ˄ ¬p p → ¬p
B S B S S
S B B S B
Tautologi Kontradiksi Kontingensi
Tautologi, Kontradiksi, dan Kontingensi

21. • Definisi 2
Proposisi majemuk p dan q disebut ekuivalen jika p↔q
merupakan tautologi. Notasi p ≡ q menunjukkan bahwa p dan q
ekuivalen.
Ekuivalensi Logika
p q p v q ¬(p v q) ¬p ¬q ¬p ˄ ¬q
¬(p v q) ↔ (¬p ˄ ¬q)
B B B S S S S B
B S B S S B S B
S B B S B S S B
S S S B B B B B

23. Contoh :
Tunjukkan bahwa ¬(p v (¬p ˄ q)) dan ¬p ˄ ¬q ekuivalen
menggunakan hukum-hukum yang ada pada tabel 6!

24. Proposisi yang satisfiable
Proposisi majemuk disebut satisfiable jika terdapat satu
penugasan nilai kebenaran variabel-variabelnya sehingga
proposisi itu bernilai benar. Jika tidak ada penugasan yang
membuat proposisi itu benar maka disebut unsatisfiable.
Contoh :
Tentukan apakah setiap gabungan proposisi berikut satisfiable!
a. (p v ¬q) ˄ (q v ¬r) ˄ (r v ¬p)
b. (p v q v r) ˄ (¬p v ¬q v ¬r) dan
c. (p v ¬q) ˄ (q v ¬r) ˄ (r v ¬p) ˄ (p v q v r) ˄ (¬p v ¬q v ¬r)
a. (p v ¬q) ˄ (q v ¬r) ˄ (r v ¬p) bernilai benar apabila p,q,r memiliki nilai
kebenaran yang sama. Jadi, (p v ¬q) ˄ (q v ¬r) ˄ (r v ¬p) satisfiable
karena terdapat satu penugasan yang membuat proposisi itu benar.
b. (p v q v r) ˄ (¬p v ¬q v ¬r) bernilai benar apabila terdapat salah satu
dari p,q,r bernilai benar dan terdapat salah satu dari p,q,r bernilai salah.
Jadi (p v q v r) ˄ (¬p v ¬q v ¬r) satisfiable karena terdapat satu
penugasan yang membuat proposisi itu bernilai benar.

25. c. (p v ¬q) ˄ (q v ¬r) ˄ (r v ¬p) bernilai benar apabila p,q,r memiliki nilai
kebenaran yang sama, sedangkan (p v q v r) ˄ (¬p v ¬q v ¬r) bernilai
benar apabila terdapat salah satu dari p,q,r bernilai benar dan terdapat
salah satu dari p,q,r bernilai salah. Terdapat kontradiksi pada nilai p,q,r.
Jadi (p v ¬q) ˄ (q v ¬r) ˄ (r v ¬p) ˄ (p v q v r) ˄ (¬p v ¬q v ¬r)
unsatisfiable karena tidak terdapat penugasan yang membuat proposisi itu
bernilai benar.

26. Contoh Penerapan Satisfiable
Contoh penerapan satisfiable terdapat pada salah satu game logika
bernama sudoku. Untuk memahami tentang game sudoku,
perhatikan video berikut!

27. 1.4 Predikat dan Kuantor
Predikat
x > 3
Subjek Predikat
P(x) = x > 3
Fungsi Proposisi

28. Contoh :
Misalkan Q(x,y) menyatakan pernyatan “x=y+3”. Tentukan
nilai kebenaran dari proposisi Q(1,2) dan Q(3,0)!
Untuk menguji Q(1,2) substitusikan x=1 dan y=2 ke pernyataan
Q(x,y).
Karena Q(1,2) menyatakan “1=2+3” maka Q(1,2) bernilai salah.
Karena Q(3,0) menyatakan “3=0+3” maka Q(3,0) bernilai benar.

29. Kuantor
Ketika variabel-variabel yang ada di fungsi proposisi
menghasilkan beberapa nilai, proposisinya mempunyai
beberapa nilai kebenaran. Untuk menyatakan nilai
kebenaran dari fungsi proposisi ini digunakan konsep
kuantifikasi. Kuantifikasi menyatakan predikat mana yang
benar dari elemen hasil. Kita akan fokus membahas dua
jenis kuantor. Kuantor universal yang menyatakan predikat
benar untuk setiap elemen yang memenuhi. Kuantor
eksistensial menyatakan terdapat satu atau lebih elemen
yang memenuhi yang membuat predikat menjadi benar.

30. Kuantor Universal
Definisi 1
Kuantor universal dari P(x) adalah pernyataan
“P(x) untuk semua nilai x yang ada di domain”
Notasi ∀ xP(x) menyatakan kuantor universal P(x). ∀
melambangkan kuantor universal. ∀ xP(x) dibaca untuk
semua x P(x)” atau untuk setiap x P(x).” Sebuah elemen
yang membuat P(x) salah disebut contoh penyangkal dari
∀xP(x).

31. Contoh 1 :
Misalkan P(x) adalah pernyataan “x+1>x” Apakah nilai kebenaran kuantor
∀xP(x) dengan domain terdiri dari semua bilangan real?
Karena P(x) benar untuk semua bilangan real x, maka kuantor ∀xP(x)
benar.
Contoh 2 :
Misalkan Q(x) adalah pernyataan “x < 2” Apakah nilai kebenaran
kuantor ∀xQ(x) dengan domain terdiri dari semua bilangan real?
Q(x) tidak benar untuk semua bilangan real x karena Q(3) bernilai salah.
Jadi x=3 merupakan contoh penyangkal untuk pernyataan ∀xQ(x)
sehingga ∀xQ(x) bernilai salah.
Mencari contoh penyangkal untuk kuantor universal penting dalam
pembelajaran matematika. Ketika semua elemen domain dituliskan
sebagai 𝑥1, 𝑥2, ...., 𝑥 𝑛, maka ∀xP(x) sama dengan konjugasi P(𝑥1) ˄
P(𝑥2) ˄ … ˄ P(𝑥 𝑛). Konjugasi bernilai benar jika dan hanya jika P(𝑥1),
P(𝑥2), … . ,P(𝑥 𝑛) semua benar.

32. Kuantor Eksistensial
Definisi 2
Kuantor eksistensial dari P(x) adalah proposisi
“Terdapat sebuah elemen x di domain sehingga P(x)”
Notasi ∃xP(x) untuk menyatakan kuantor eksistensial dari
P(x). ∃ disebut kuantor eksistensial.

33. Contoh 1 :
Misalkan P(x) menyatakan “x > 3” Apakah nilai kebenaran dari ∃xP(x)
dengan domain terdiri dari semua bilangan real?
Karena x>3 bernilai benar untuk nilai x tertentu seperti x=4, maka ∃xP(x)
benar.
Contoh 2 :
Misalkan Q(x) menyatakan “x=x+1”. Apakah nilai kebenaran ∃xQ(x)
dengan domain terdiri dari semua bilangan real?
Karena Q(x) bernilai salah untuk setiap bilangan real x, kuantor
eksistensial ∃xQ(x) salah.
Ketika semua elemen domain dituliskan sebagai 𝑥1, 𝑥2, ...., 𝑥 𝑛, kuantor
eksistensial ∃xP(x) sama dengan disjungsi P(𝑥1) v P(𝑥2) v ... v P(𝑥 𝑛).
Disjungsi bernilai benar jika dan hanya jika salah satu dari P(𝑥1),
P(𝑥2), … . ,P(𝑥 𝑛) benar.

34. Kuantor
Pernyataan Kapan bernilai benar? Kapan bernilai salah?
∀xP(x) P(x) benar untuk setiap x Terdapat satu x yang
membuat P(x) salah
∃xP(x) Terdapat satu x yang
membuat P(x) benar
P(x) salah untuk setiap
x
Kuantor yang Bersifat Unik
Kita telah mempelajari kuantor universal dan kuantor
eksistensial. Terdapat kuantor bersifat unik yang
dilambangkan ∃! yang dapat dinyatakan dengan “terdapat
tepat sebuah x yang membuat P(x) benar.
Contoh: ∃!x(x-1=0). Nilai x yang memenuhi hanya x=1.

35. Kuantor Dengan Domain Terbatas
Apa maksud dari pernyataan ∀x<0 (𝑥2
>0), ∀y ≠0 (𝑦3
≠0),
dan ∃z>0 (𝑧2
=2) dengan domain terdiri dari bilangan real?
Pernyataan ∀x<0 (𝑥2
>0) menyatakan bahwa untuk setiap
bilangan real x dengan x<0, 𝑥2
>0. Dengan kata lain,
“kuadrat dari bilangan real negatif adalah positif.
Pernyataan ini sama dengan ∀x(x<0 → 𝑥2
>0)
Pernyataan ∀y ≠ 0 ( 𝑦3 ≠ 0) menyatakan bahwa untuk
setiap bilangan real y dengan y≠0, berlaku 𝑦3
≠0. Dengan
kata lain, “pangkat tiga dari setiap bilangan real tak nol
adalah bilangan tak nol.” Pernyataan ini sama dengan
∀y(y ≠0 → 𝑦3
≠0).
Pernyataan ∃z >0 ( 𝑧2
=2) menyatakan bahwa terdapat
sebuah bilangan real z dengan z>0, sehingga 𝑧2
=2.
Dengan kata lain, “terdapat akar 2 positif.” Pernyataan ini
sama dengan ∃z(z > 0 ˄ 𝑧2
=2)

36. Precedence (prioritas) Kuantor
Kuantor ∀ dan ∃ mempunyai prioritas tertinggi daripada semua operator
logika berdasarkan kalkulus proposisi. Misalkan ∀xP(x) v Q(x) adalah
disjungsi antara ∀xP(x) dan Q(x). Dengan kata lain, (∀xP(x)) v Q(x), bukan
∀x (P(x) v Q(x))
Variabel Terikat
Ketika sebuah kuantor digunakan untuk variabel x, maka dapat dikatakan
variabel ini terbatas. Variabel yang tidak terikat oleh kuantor atau dibuat
sama dengan nilai tertentu disebut variabel bebas.
Contoh : ∃x(x+y=1). Variabel x terikat pada kuantor ∃x, tetapi y adalah
variabel bebas karena tidak terikat kuantor dan tidak nilai yang membatasi
varibel ini.

37. Logika Ekuivalen yang Mengandung Kuantor
Pernyataan yang mengandung predikat dan kuantor termasuk logika
ekuivalen jika dan hanya jika mereka memiliki nilai kebenaran yang sama,
tidak masalah predikat mana yang disubtitusikan ke pernyataan ini dan
domain mana yang digunakan untuk variabel pada fungsi proposisi. Kita
gunakan notasi S ≡ T untuk menyatakan dua pernyataan S dan T yang
mengandung predikat dan kuantor adalah logika ekuivalen.
Contoh:
Tunjukkan bahwa ∀x(P(x) ˄ Q(x)) dan ∀xP(x) ˄ ∀xQ(x) logika ekuivalen.
Misalkan kita memiliki predikat P dan Q dengan domain yang sama. Kita
tunjukkan dengan dua cara yaitu jika ∀x(P(x) ˄ Q(x)) benar maka ∀xP(x) ˄
∀xQ(x) benar. Lalu jika ∀xP(x) ˄ ∀xQ(x) benar maka ∀x(P(x) ˄ Q(x))
benar.
Misalkan ∀x(P(x) ˄ Q(x)) benar, berarti jika a di domain maka P(a) ˄ Q(a)
benar. Jadi P(a) benar dan Q(a) benar. Karena P(a) benar Q(a) benar
untuk setiap elemen domain, dapat disimpulkan ∀xP(x) ˄ ∀xQ(x) benar.
Kemudian misalkan ∀xP(x) ˄ ∀xQ(x) benar, berarti ∀xP(x) benar dan
∀xQ(x) benar. Karena a ada di domain maka P(a) benar dan Q(a) benar.
Jadi untuk semua a, P(a) ˄ Q(a) benar maka ∀x(P(x) ˄ Q(x)) benar.
Dengan demikian ∀x(P(x) ˄ Q(x)) ≡ ∀xP(x) ˄ ∀xQ(x).

38. Negasi Pernyataan Berkuantor
Untuk memahami bentuk negasi dari pernyataan berkuantor, coba pahami
contoh berikut.
Contoh :
Semua mahasiswa di kelas ini telah mengikuti mata kuliah kalkulus.
Jika kita tuliskan bentuk kuantornya menjadi ∀xP(x) dengan P(x) adalah
pernyataan x telah mengikuti mata kuliah kalkulus dan domain x adalah
mahasiswa di kelas ini. Negasi dari pernyataan tersebut adalah “Tidak
benar bahwa semua mahasiswa di kelas ini telah mengikuti mata kuliah
kalkulus. Dengan kata lain terdapat mahasiswa di kelas ini yang belum
mengikuti mata kuliah kalkulus. Pernyataan ini adalah bentuk dari kuantor
∃x¬P(x). Dengan demikian, ¬∀xP(x) ≡ ∃x¬P(x).

39. Contoh Penerapan Kuantor dari Lewis Carroll
Semua singa adalah hewan buas
Beberapa singa tidak minum kopi
Beberapa hewan buas tidak minum kopi
Misalkan :
p : x adalah singa
q : x adalah hewan buas
r : x minum kopi
∀x(P(x) → Q(x))
∃x(P(x) ˄ ¬R(x))
∃x(Q(x) ˄ ¬R(x))

40. 1.5 Kuantor Bersusun
Setelah mempelajari beberapa macam kuantor pada sesi 1.4, kita akan
belajar tentang kuantor bersusun. Kuantor bersusun banyak digunakan
dalam pernyataan matematika. Konsep-konsep kuantor yang telah kita
pelajari pada sesi 1.4 merupakan dasar untuk memahami konsep
kuantor bersusun.
Memahami Kalimat yang Mengandung Kuantor Bersusun
Perhatikan contoh-contoh penggunaan kuantor bersusun pada
pernyataan matematika berikut!
Asumsikan domain x dan y adalah bilangan real

41. Urutan Kuantor-Kuantor
Misalkan Q(x,y) menyatakan “x+y=0”. Bagaimana nilai kebenaran kuantor
bersusun ∃y∀xQ(x,y) dan ∀x∃yQ(x,y)?
∃y∀xQ(x,y) menyatakan bahwa terdapat bilangan real y sehingga untuk
setiap bilangan real x berlaku Q(x,y). Berapapun nilai y yang dipilih maka
terdapat satu nilai x yang memenuhi x+y=0. Karena tidak ada bilangan
real y yang dapat memenuhi x+y=0 untuk setiap bilangan real x maka
pernyataan ∃y∀xQ(x,y) salah.
∀x∃yQ(x,y) menyatakan bahwa untuk setiap bilangan real x maka
terdapat bilangan real y berlaku Q(x,y). Diberikan sebuah bilangan real x
maka terdapat satu bilangan real y sehingga berlaku x+y=0. Nilai y = -x.
Dengan demikian ∀x∃yQ(x,y) benar
Berdasarkan contoh ini maka dapat dilihat bahwa ∃y∀xQ(x,y)
dan ∀x∃yQ(x,y) tidak ekuivalen.

43. Menerjemahkan Pernyataan Matematika ke Dalam Pernyataan yang
Mengandung Kuantor Bersusun.
Gunakan kuantor untuk menyatakan definisi limit fungsi bernilai real f(x) dari
variabel real x pada titik a di domain!
Definisi lim
𝑥→𝑎
𝑓(𝑥) = L adalah untuk setiap bilangan real 𝜀>0 terdapat bilangan
real 𝛿>0 sehingga 𝑓 𝑥 − 𝐿 < 𝜀 apabila 0< 𝑥 − 𝑎 <𝛿 .
Bentuk kuantornya adalah ∀𝜀∃𝛿∀𝑥(0< 𝑥 − 𝑎 <𝛿 → 𝑓 𝑥 − 𝐿 < 𝜀).
Dapat pula ditulis sebagai ∀𝜀 > 0∃𝛿 > 0∀𝑥(0< 𝑥 − 𝑎 <𝛿 → 𝑓 𝑥 − 𝐿 < 𝜀).

44. Menerjemahkan Kuantor Bersusun ke Kalimat Biasa
Terjemahkan kuantor bersusun berikut
C(x) menyatakan “x mempunyai komputer”
F(x,y) menyatakan “x dan y adalah teman”
Domain x dan y adalah siswa di sekolahmu
Makna dari kuantor tersebut adalah untuk setiap siswa x di
sekolahmu, x mempunyai komputer atau terdapat siswa y
sehingga y mempunyai komputer dan x dan y berteman.
Dengan kata lain, setiap siswa di sekolahmu mempunyai
komputer atau punya teman yang mempunyai komputer.

45. Menerjemahkan Kalimat Biasa ke Kalimat Logika
Tuliskan pernyataan berikut ke dalam kalimat logika berkuantor!
Jika seseorang adalah wanita dan merupakan orang tua, maka orang ini
adalah ibu dari seseorang
Pernyataan tersebut dapat ditulis sebagai “Untuk setiap orang x, jika orang
x adalah wanita dan merupakan orang tua,maka terdapat orang y
sedemikian sehingga x adalah ibu dari y.
F(x) menyatakan x adalah wanita
P(x) menyatakan x adalah orang tua
M(x,y) menyatakan x adalah ibu dari y
Pernyataan tersebut menjadi ∀x((F(x) ˄ P(x)) → ∃yM(x,y)
Dapat pula ditulis sebagai ∀x∃y ((F(x) ˄ P(x)) → M(x,y))

46. Negasi Kuantor Bersusun
Gunakan kuantor dan predikat untuk menyatakan bahwa lim
𝑥→𝑎
𝑓(𝑥) tidak ada
untuk f(x) fungsi bernilai real dari variabel real x dan a di domain.
Karena lim
𝑥→𝑎
𝑓(𝑥) tidak ada maka lim
𝑥→𝑎
𝑓(𝑥) ≠ L.
Kita gunakan contoh sebelumnya tentang definisi limit.
¬∀𝜀 > 0∃𝛿 > 0∀𝑥(0< 𝑥 − 𝑎 <𝛿 → 𝑓 𝑥 − 𝐿 < 𝜀).

47. TERIMA KASIH
ATAS
PERHATIANNYA

48. SOAL-SOAL LATIHAN
Exercise 1.1 nomor 15, 27, dan 32 (hal. 14-15)
Exercise 1.2 nomor 11, 20, dan 41 (hal. 23-24)
Exercise 1.3 nomor 11, 22, dan 61 (hal. 35-36)
Exercise 1.4 nomor 7, 14, dan 34 (hal. 53-55),
Exercise 1.5 nomor 1, 19, 31 (hal. 64-67)