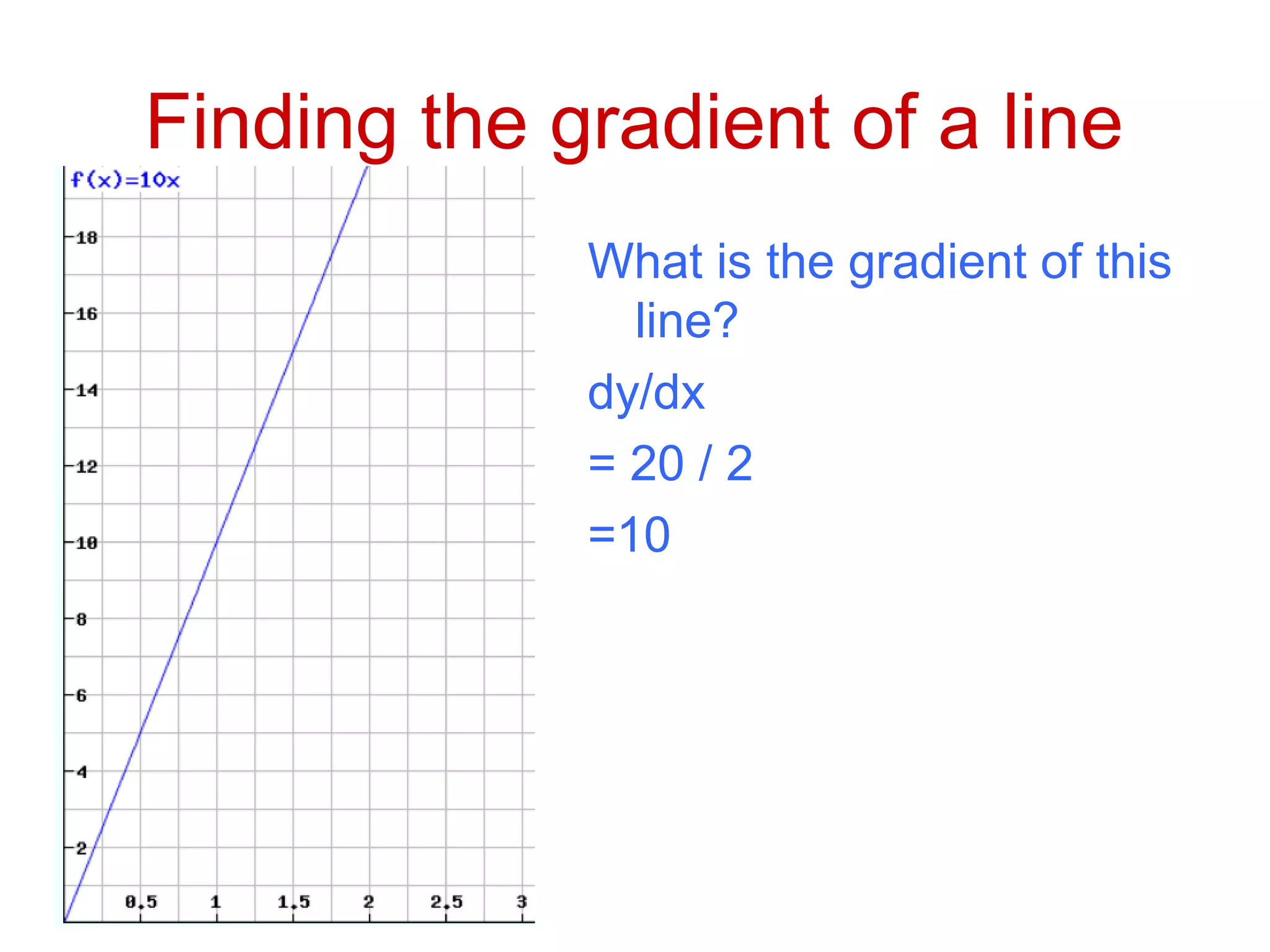
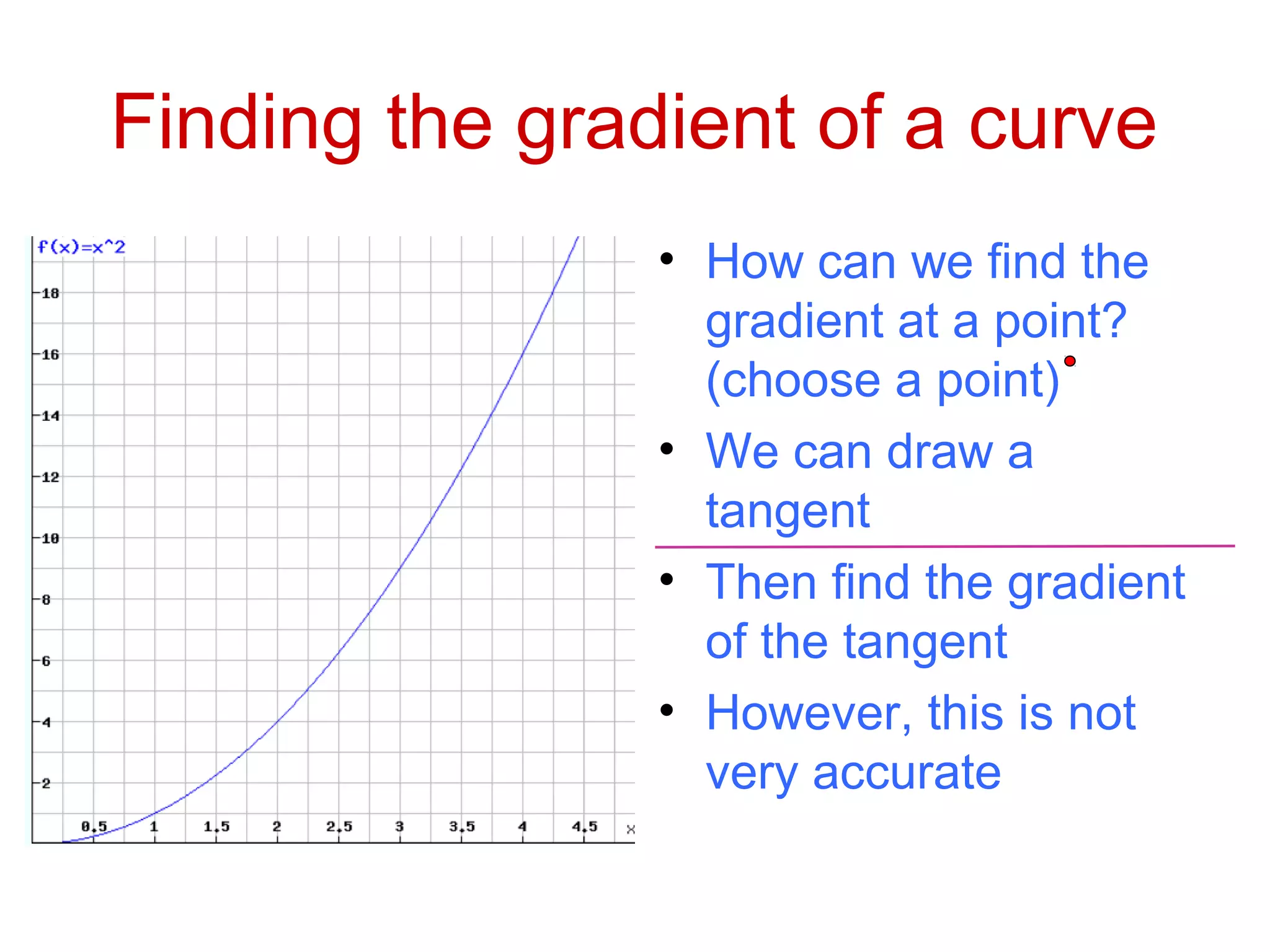
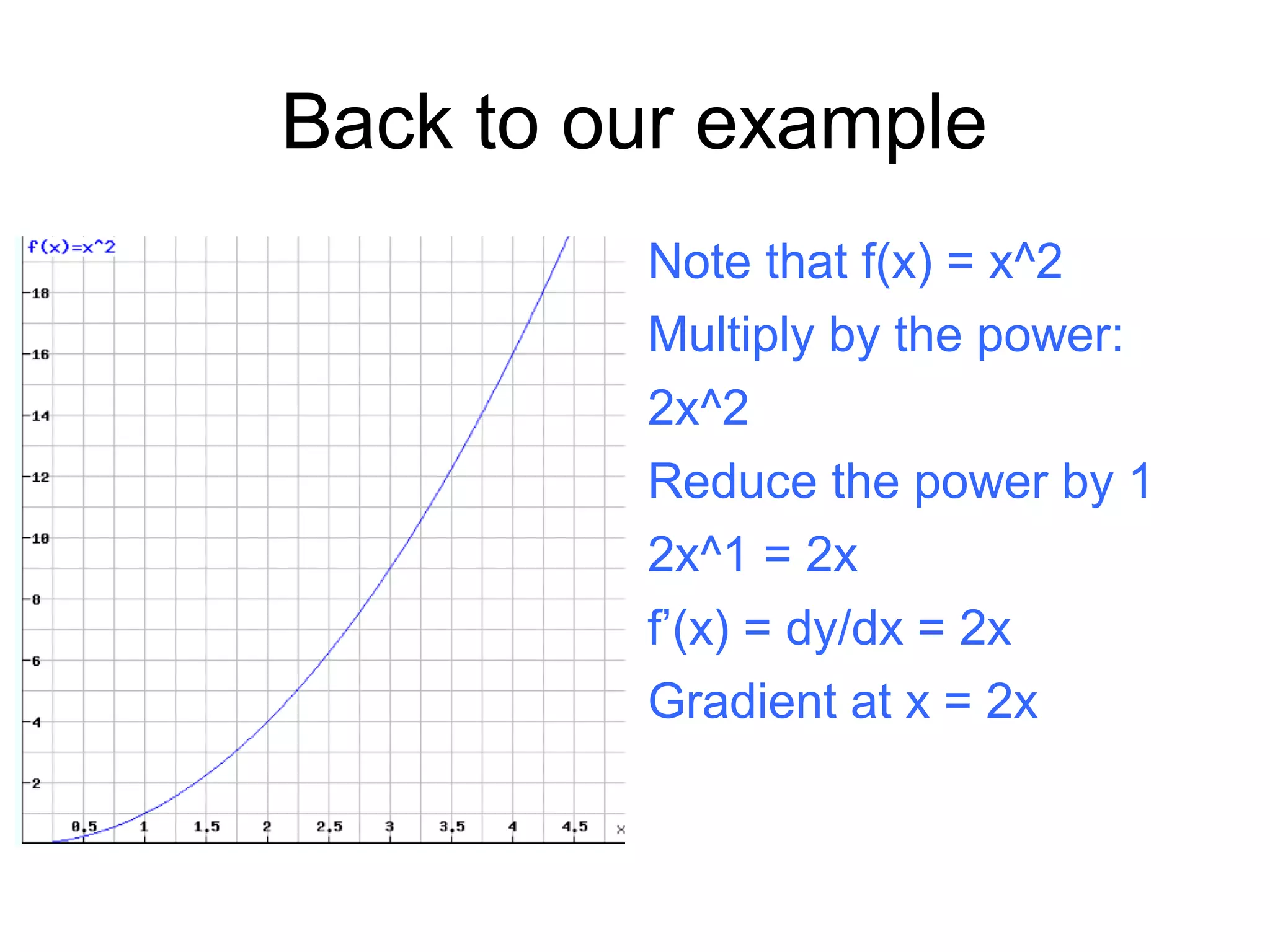
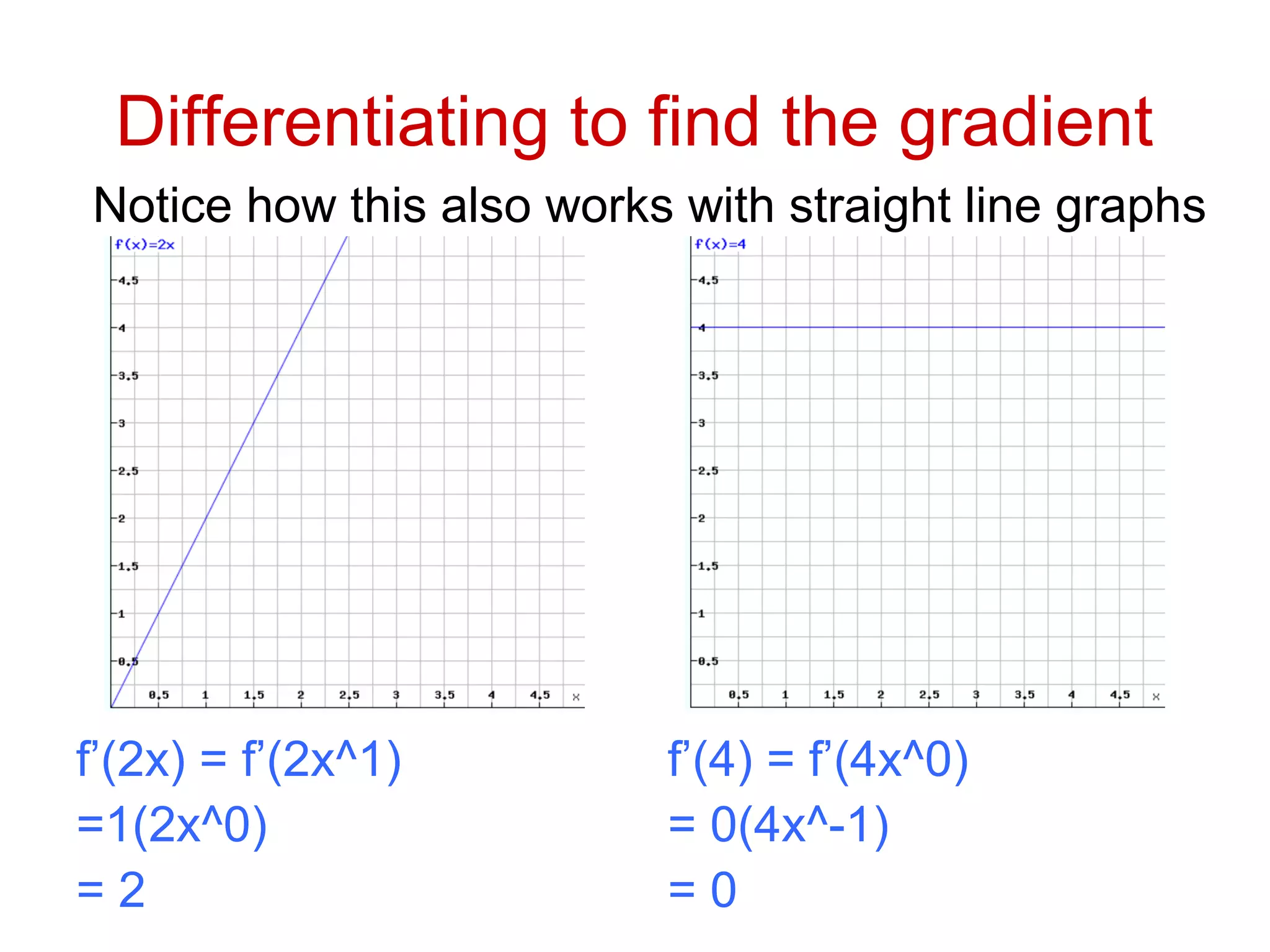
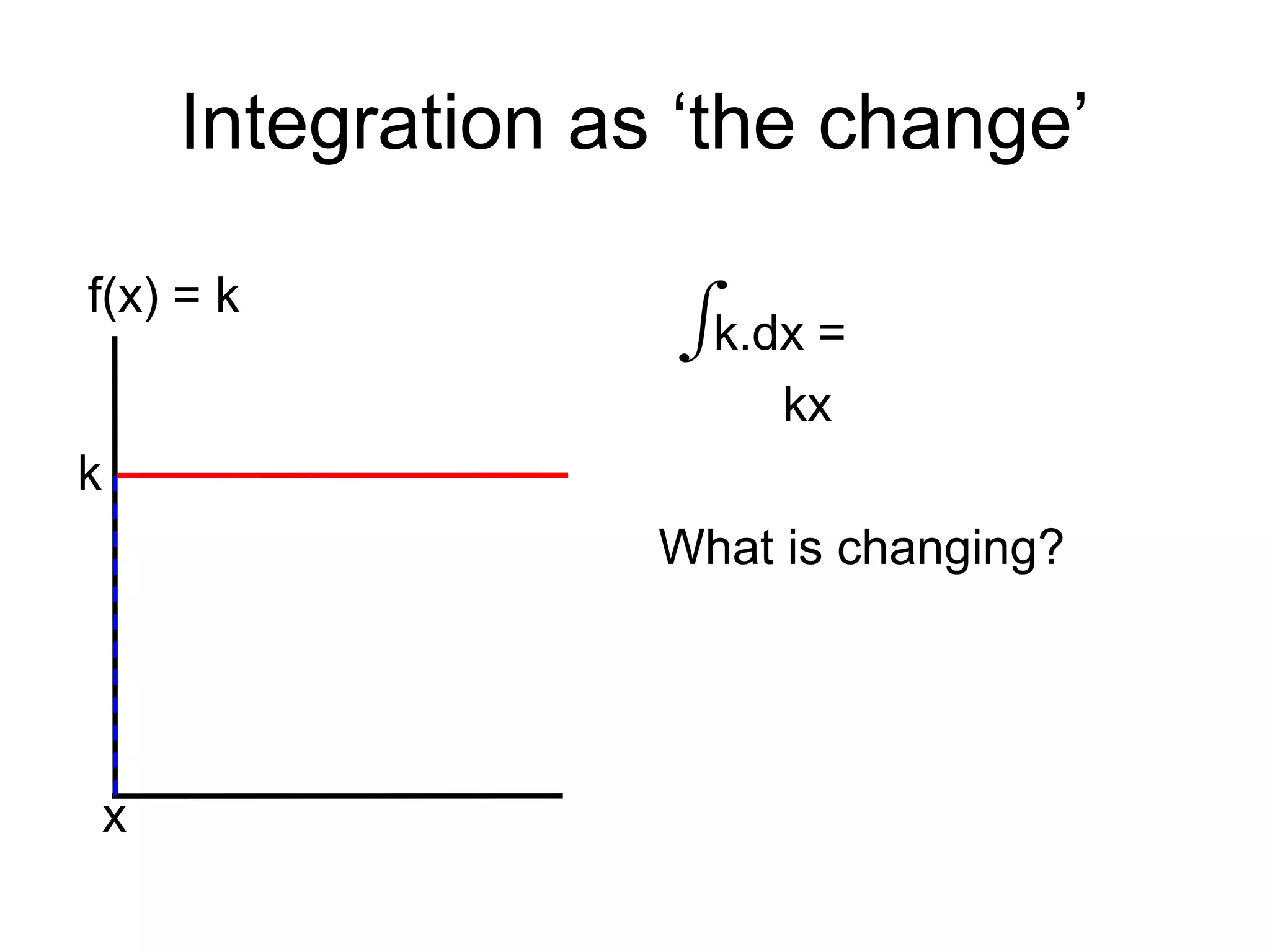
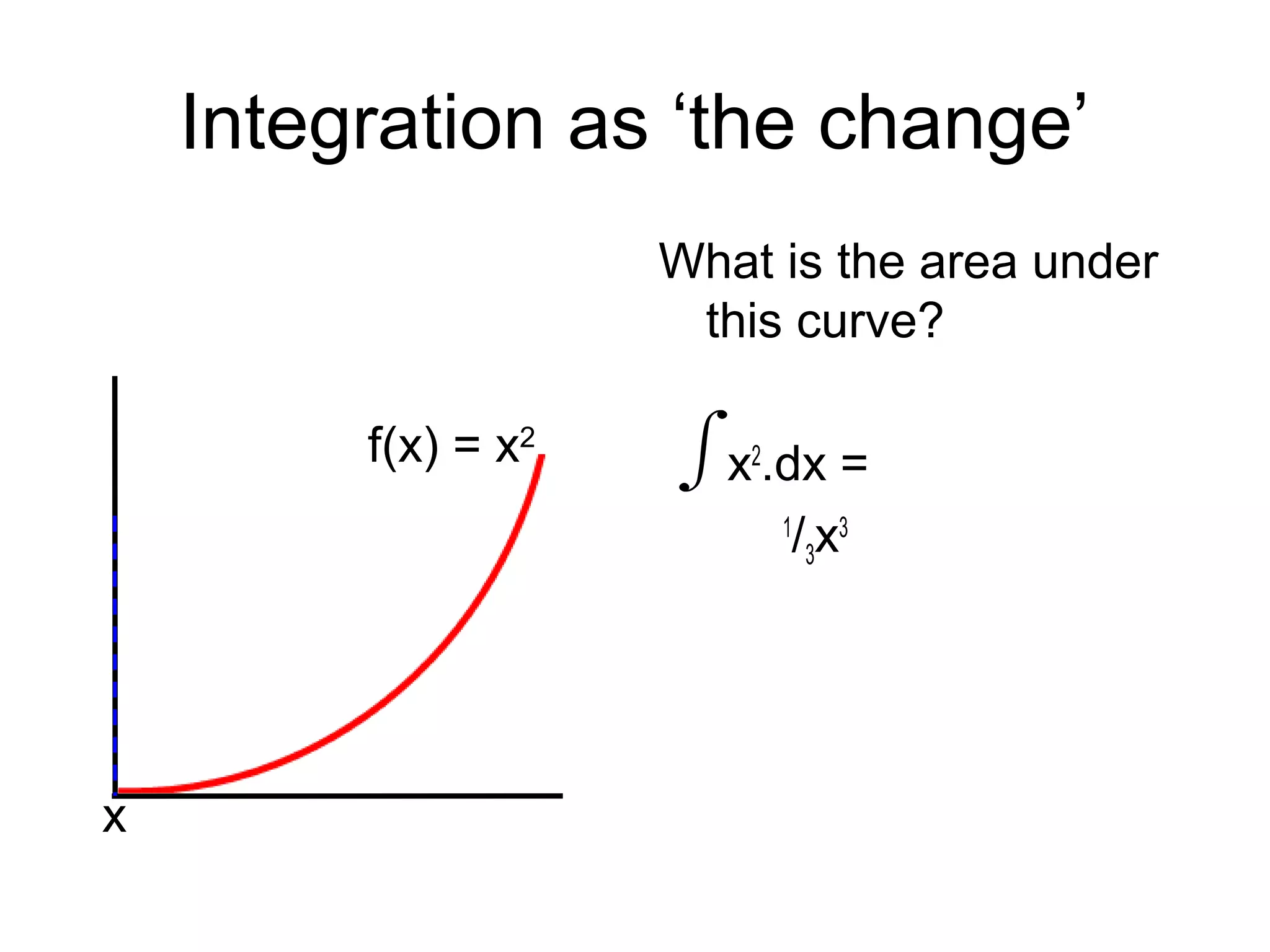
This document discusses rates of change and differentiation. It explains that differentiation finds the rate of change of a function, while integration finds the total change. Specifically, it shows that differentiation involves multiplying a function by its power and reducing the power by 1, while integration involves raising the power by 1 and dividing by the new power. Examples are provided to demonstrate finding the gradient and rate of change of linear, quadratic, and other polynomial functions using differentiation, as well as using integration to find total change over an area under a curve.

1. Rates of change

2. Rate of change
• Tell me something which …
a)Changes
b)Doesn't change
c)Changes at a constant rate
d)Changes slowly / quickly
e)Does not change at a constant rate
f) Whose rate of change is constant
g)Whose rate of change is not constant

3. Gradient as ‘rate of change’
f(x) = k
How quickly does the
height of this line
change?
It doesn’t
Hence …

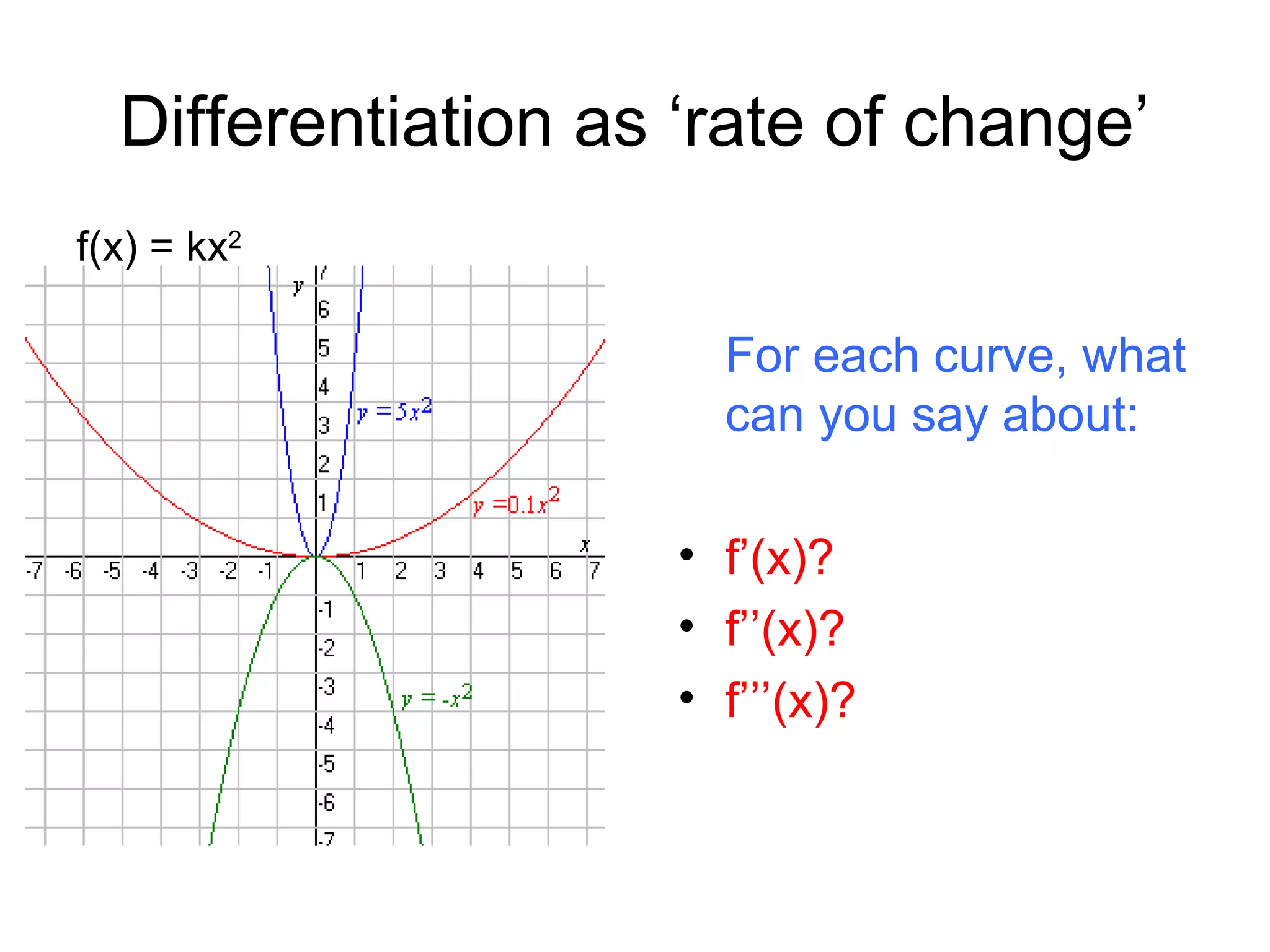
4. Differentiation as ‘rate of change’
What can you say about:
f’(x)? [the rate of change of
f(x)?]
f’’(x)? [the rate of change of
f’(x)?]
f(x) = kx
g(x) = jx

5. Differentiation as ‘rate of change’
f(x) = kx2
For each curve, what
can you say about:
• f’(x)?
• f’’(x)?
• f’’’(x)?

6. Rate of Change
x
f(x) = x2
f ’(x) = 2x
f ’’(x) = 2
f ’’’(x) = 0
1 2 3 4 5 6 7 8 9
1 4 9 16 25 36 49 64 81
3 5 7 9 11 13 15 17
2 2 2 2 2 2 2
0 0 0 0 0 0

7. Finding the gradient of a line
What is the gradient of this
line?
dy/dx
= 20 / 2
=10

8. Finding the gradient of a curve
• How can we find the
gradient at a point?
(choose a point)
• We can draw a
tangent
• Then find the gradient
of the tangent
• However, this is not
very accurate

9. Differentiating to find the gradient
• To find the gradient of
a polynomial by
differentiation …
• Multiply by the power
• Then reduce the
power by 1.
• x^n
• nx^n
• nx^(n-1)

10. Back to our example
Note that f(x) = x^2
Multiply by the power:
2x^2
Reduce the power by 1
2x^1 = 2x
f’(x) = dy/dx = 2x
Gradient at x = 2x

11. Differentiating to find the gradient
f’(2x) = f’(2x^1)
=1(2x^0)
= 2
Notice how this also works with straight line graphs
f’(4) = f’(4x^0)
= 0(4x^-1)
= 0

12. Integration (the reverse)
If DIFFERENTIATION seeks to find the rate at
which something changes
INTEGRATION seeks to find the total change that
occurs

13. For example
A man walks away from his house, and after 2
hours, finds himself 4 km away from his house.
DIFFERENTIATION finds his displacement’s
RATE OF CHANGE to be …
In contrast, a man walks away from his house for 2
hours at a rate of 2km / hr.
INTEGRATION finds his displacement’s TOTAL
CHANGE to be …

14. For example
If integration is the opposite of differentiation …
Differentiation involves:
MULTIPLYING by the power, and
REDUCING the power by 1.
Then integration involves:
RAISING the power by 1, and
DIVIDING by the new power.

15. Integration as ‘the change’
k.dx =
kx
What is changing?
f(x) = k
x
k

16. Integration as ‘the change’
f(x) = x
x.dx =
1
/2x2
Does this also apply
here?
x

17. x
Integration as ‘the change’
What is the area under
this curve?
x2
.dx =
1
/3x3
f(x) = x2