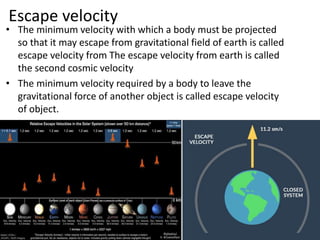
1. The document discusses key concepts of gravitation including Newton's universal law of gravitation, Kepler's laws of planetary motion, gravitational force, acceleration due to gravity, escape velocity, and free fall.
2. It explains that gravitational force is responsible for holding the atmosphere above the earth and for the motion of objects.
3. Newton's universal law of gravitation states that the gravitational force between two objects is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.