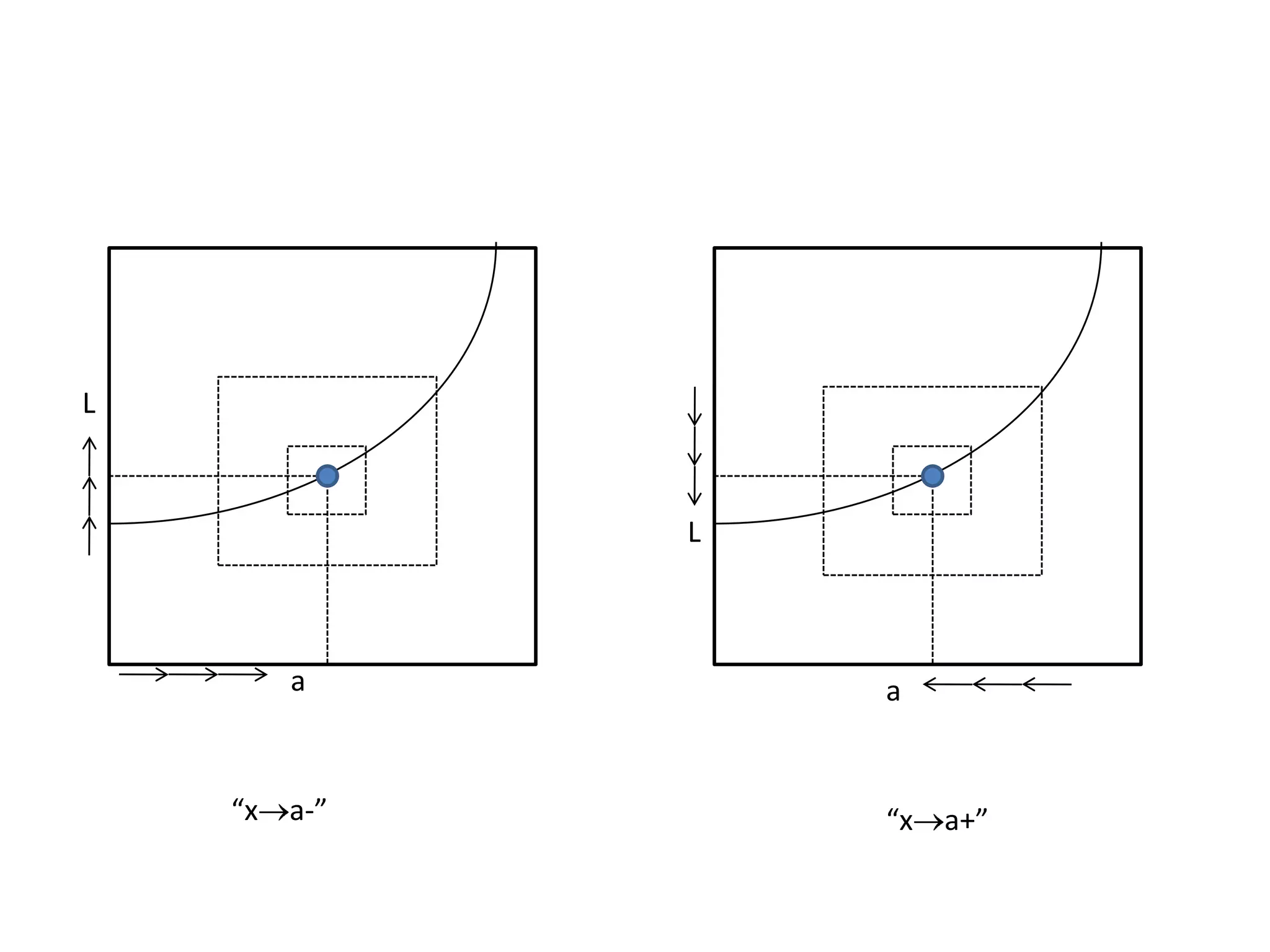
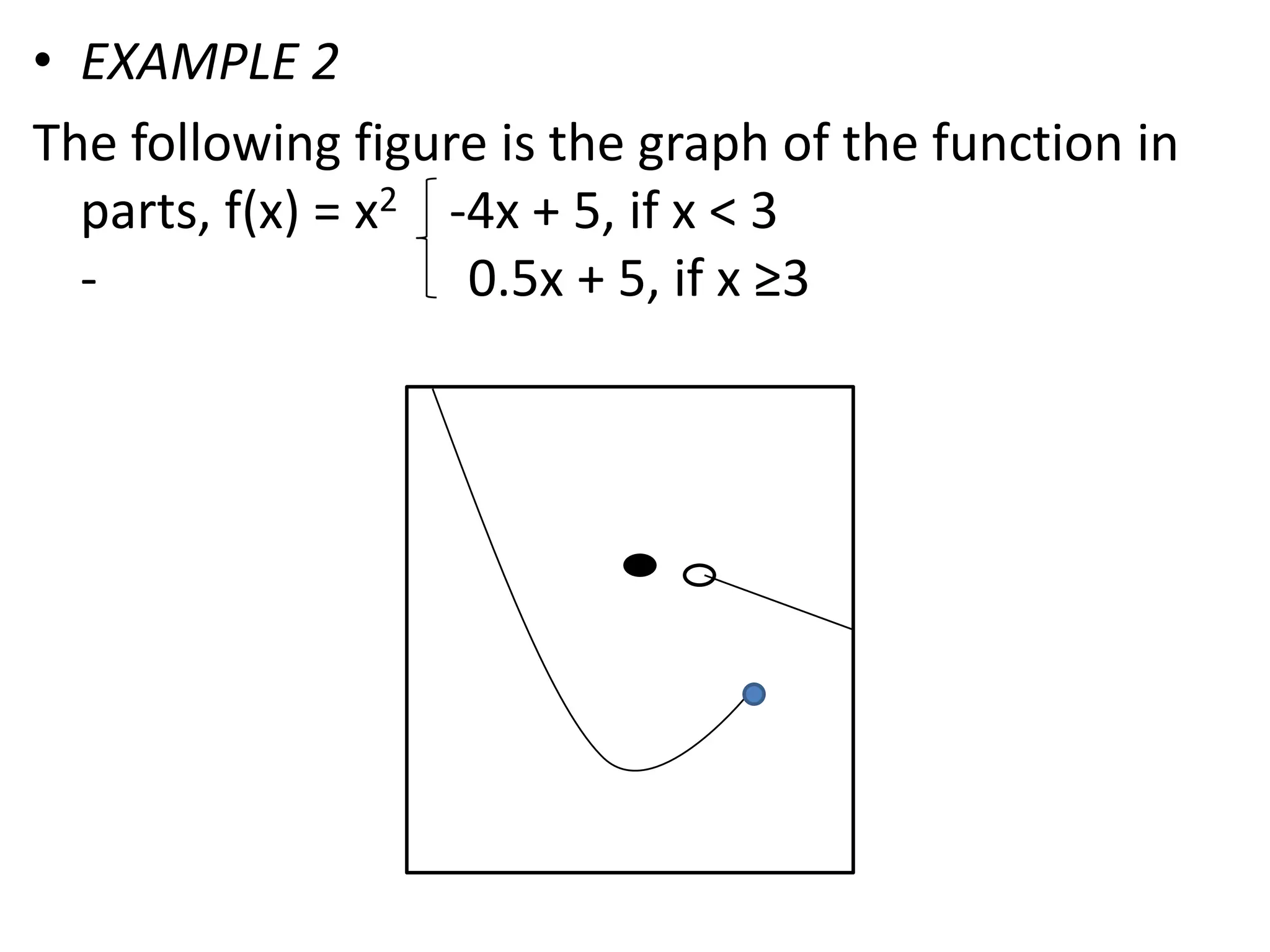
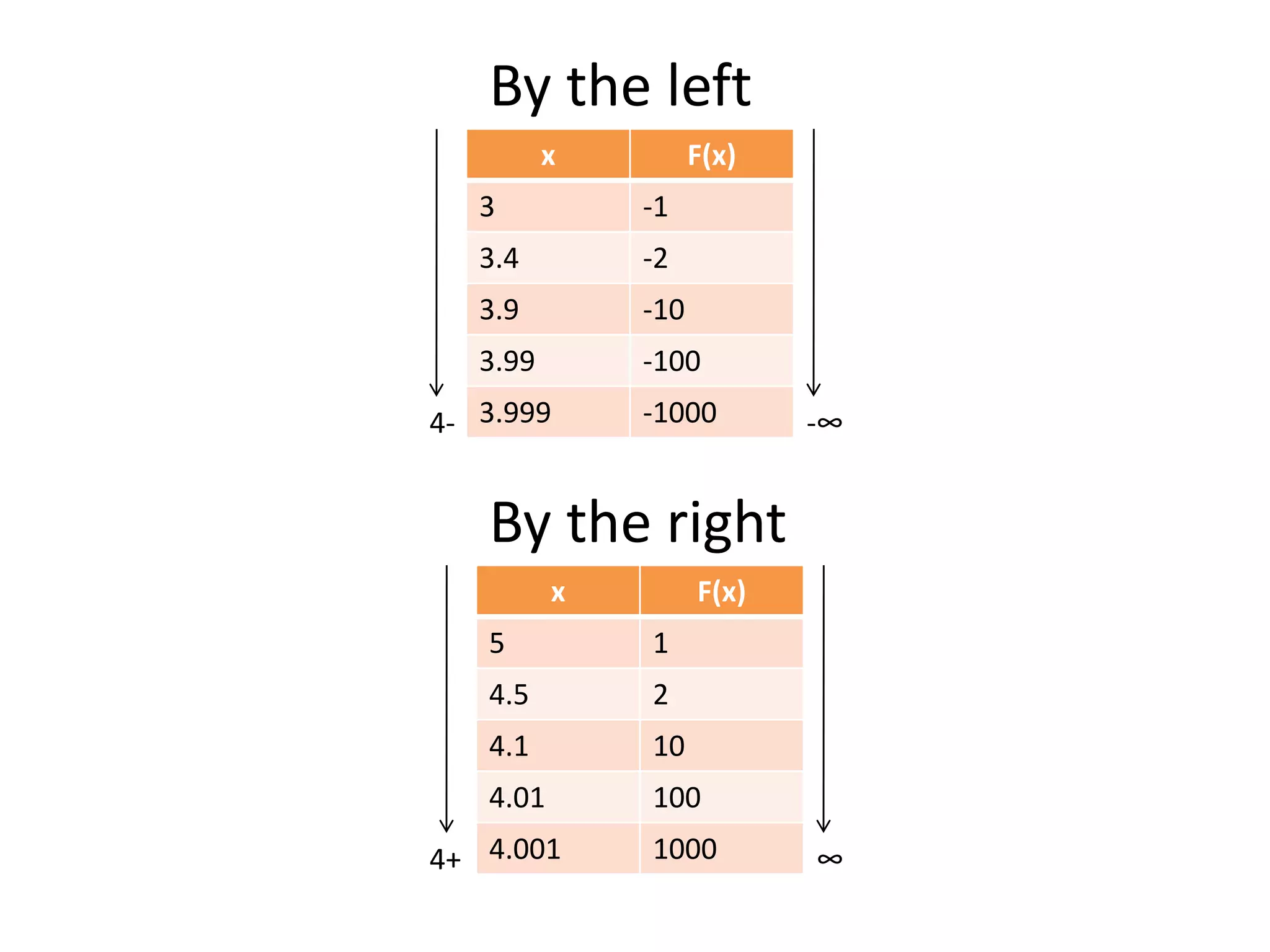
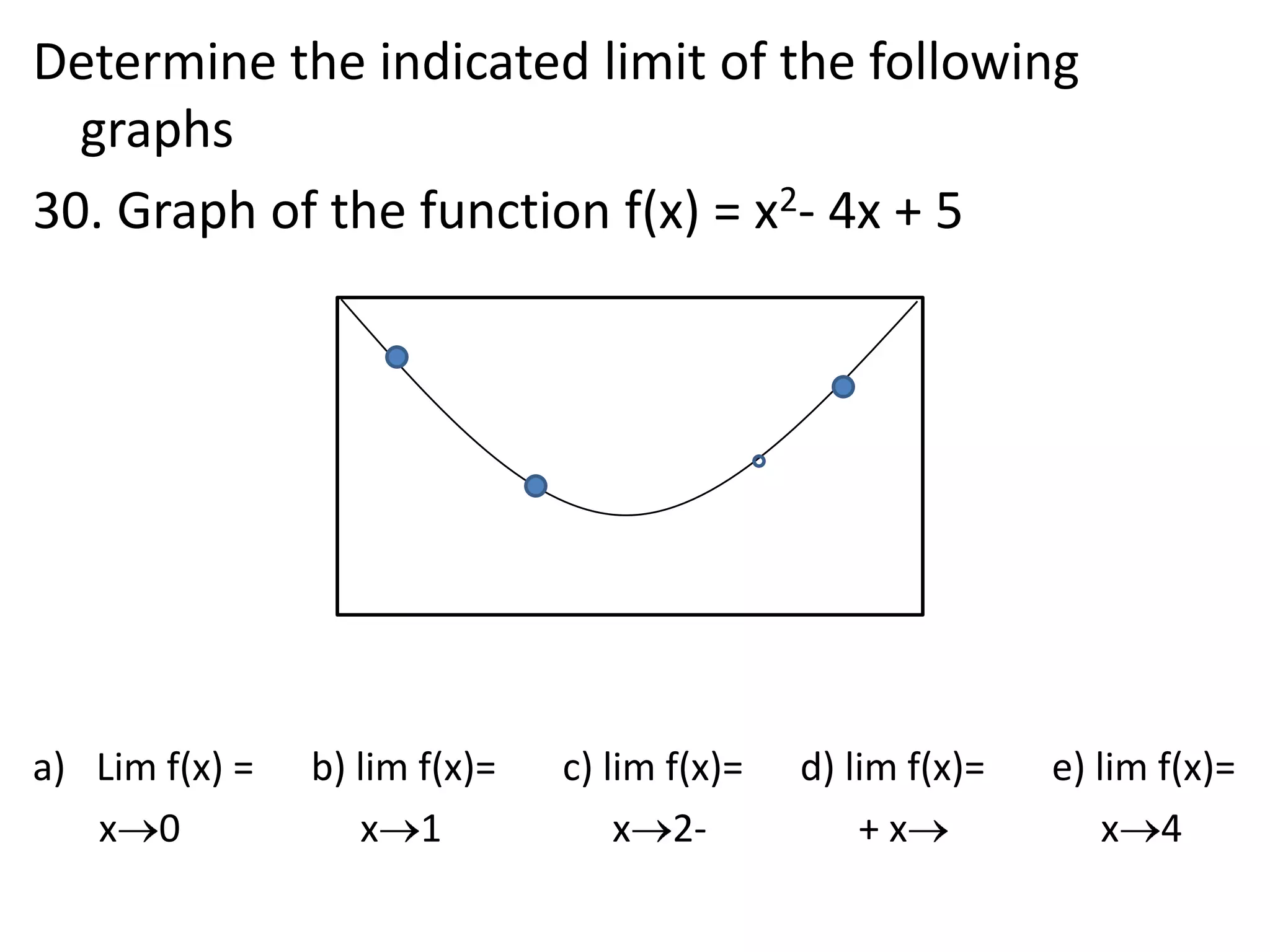
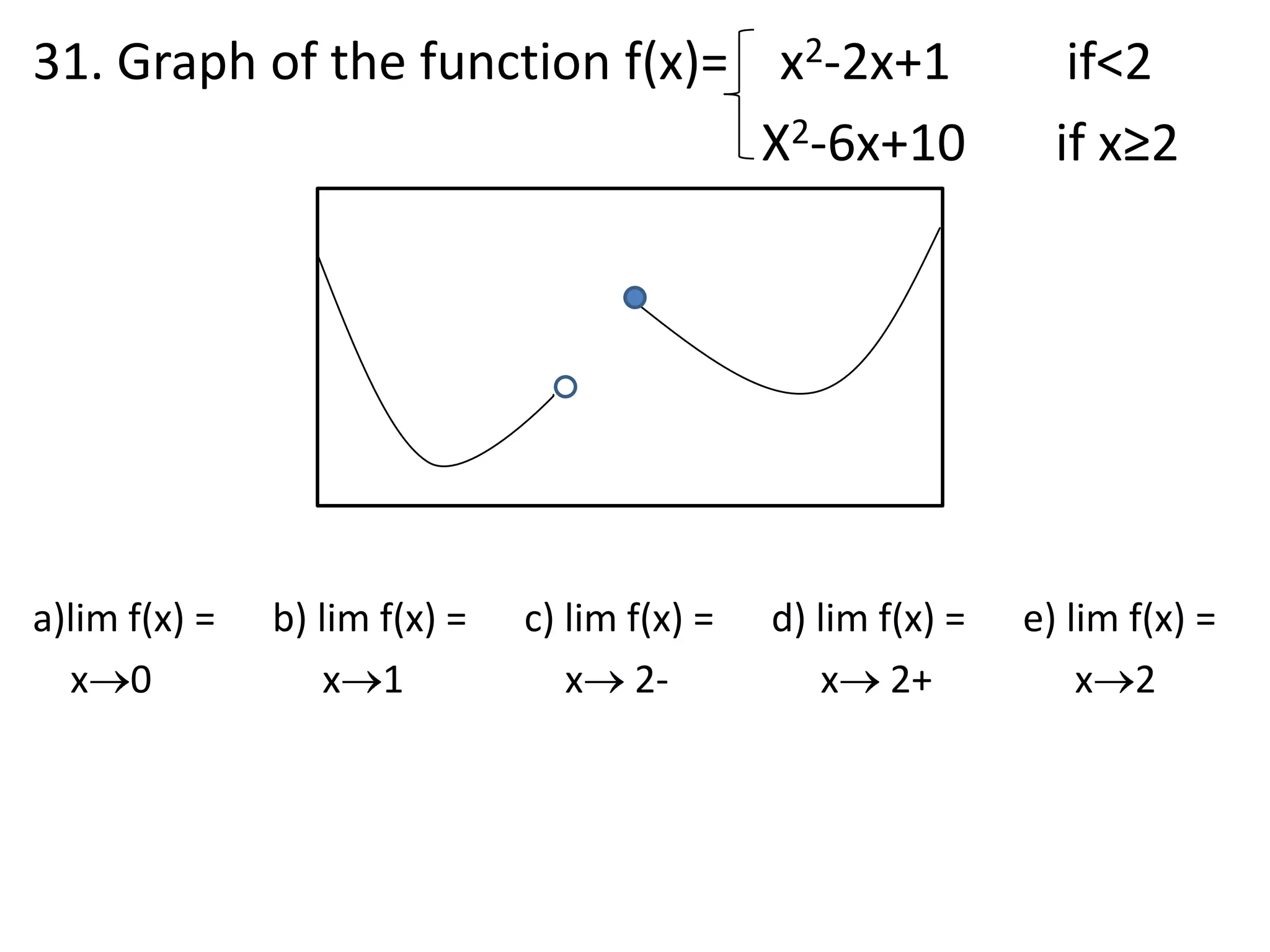
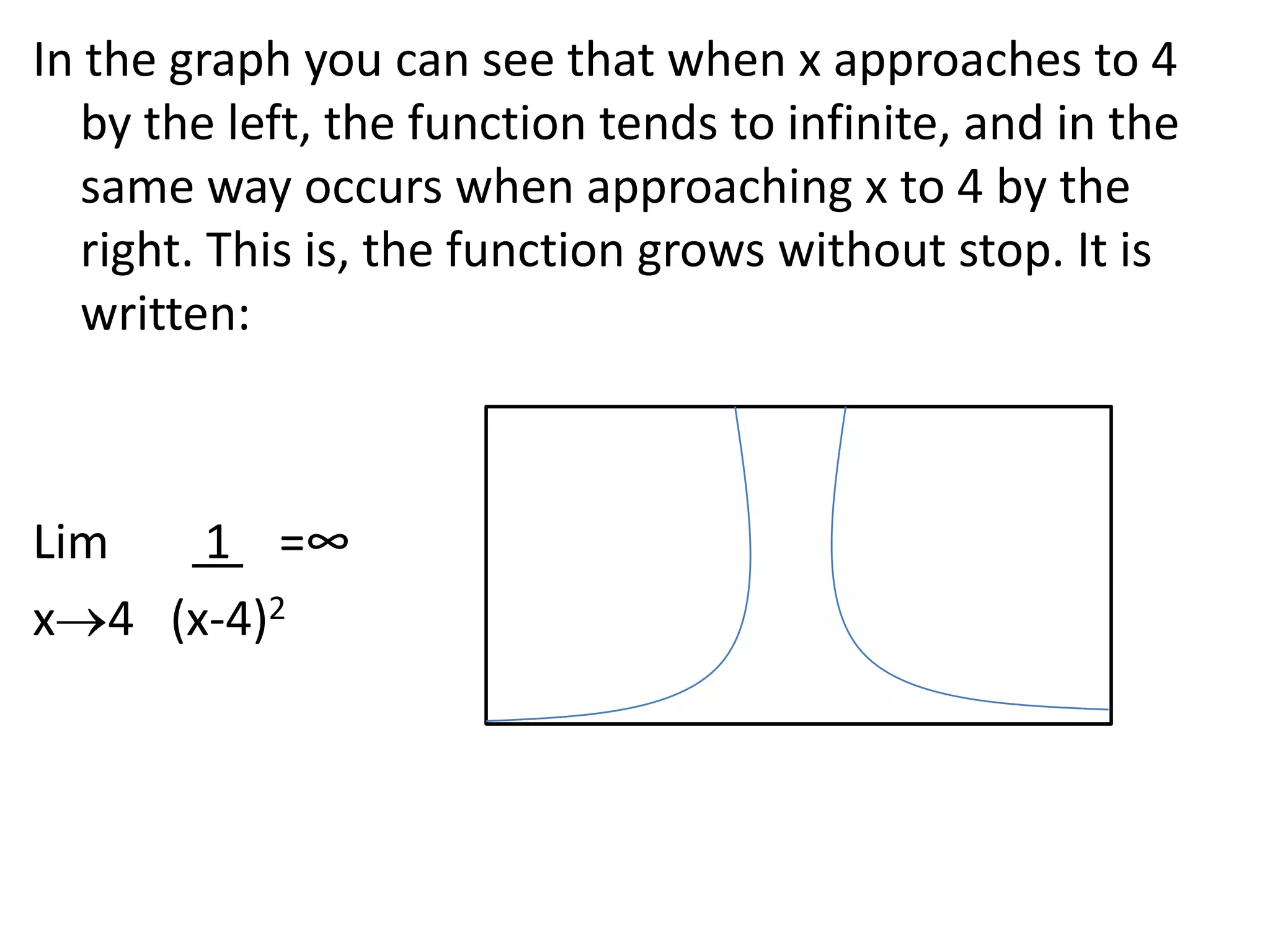
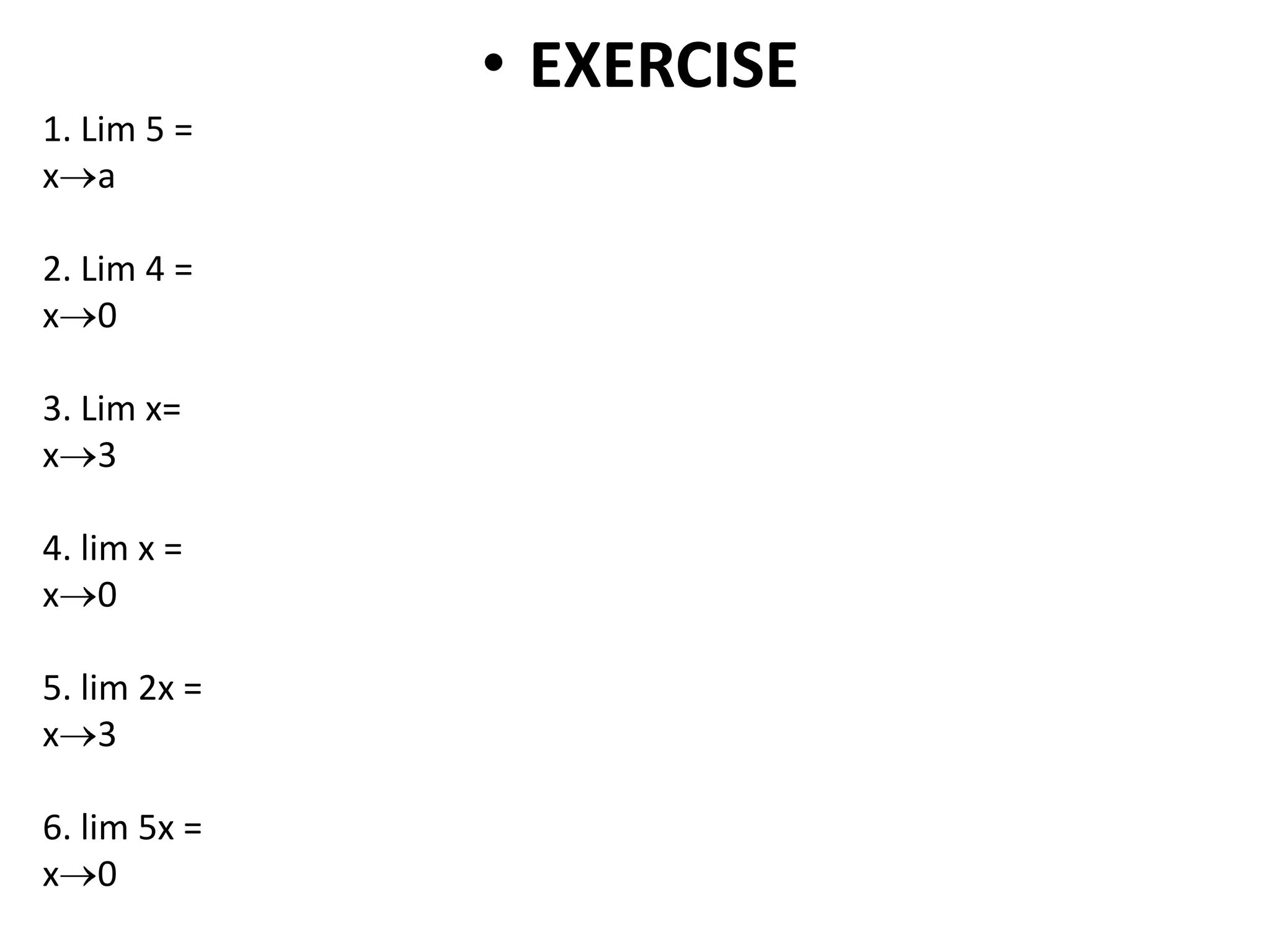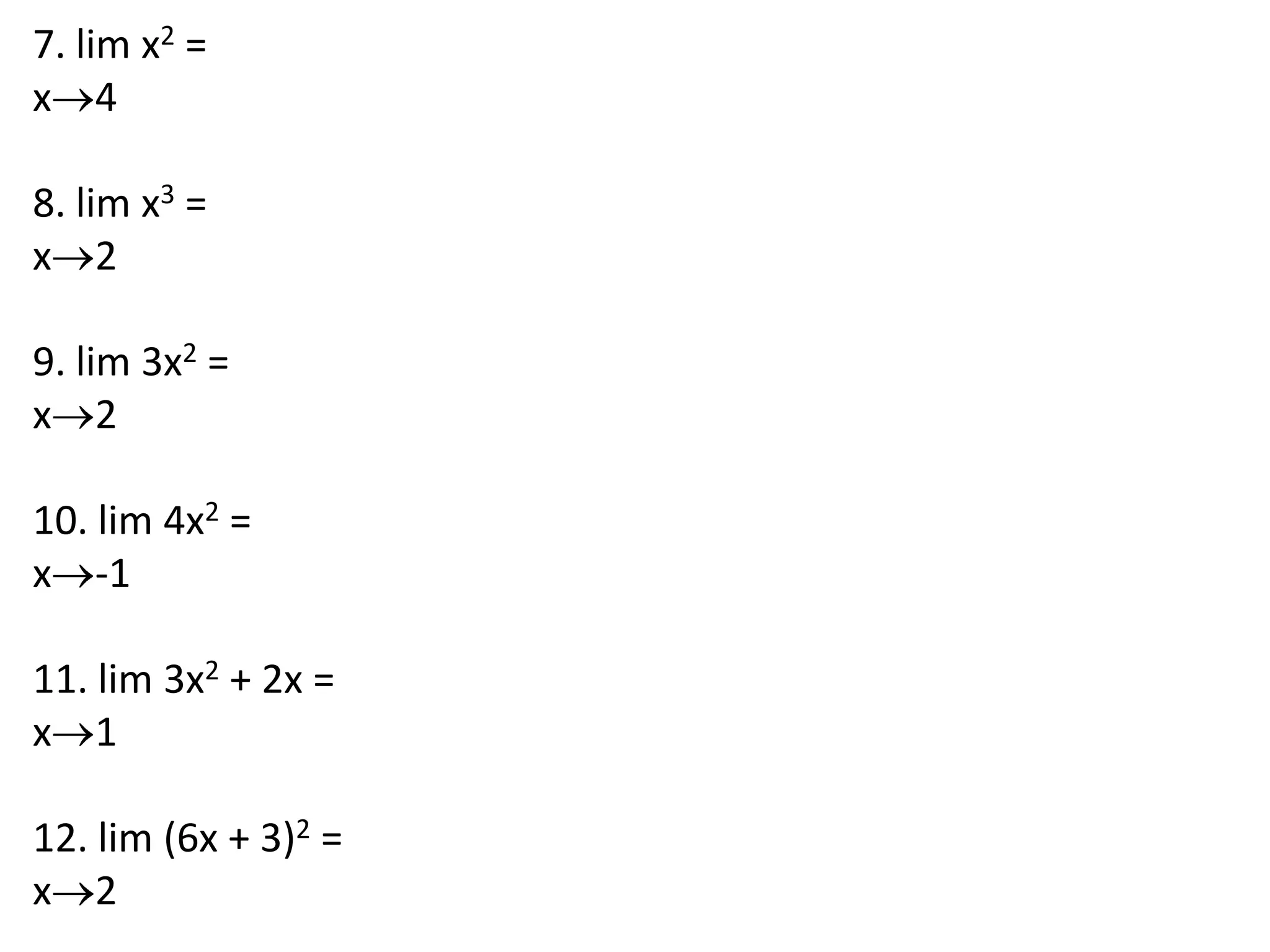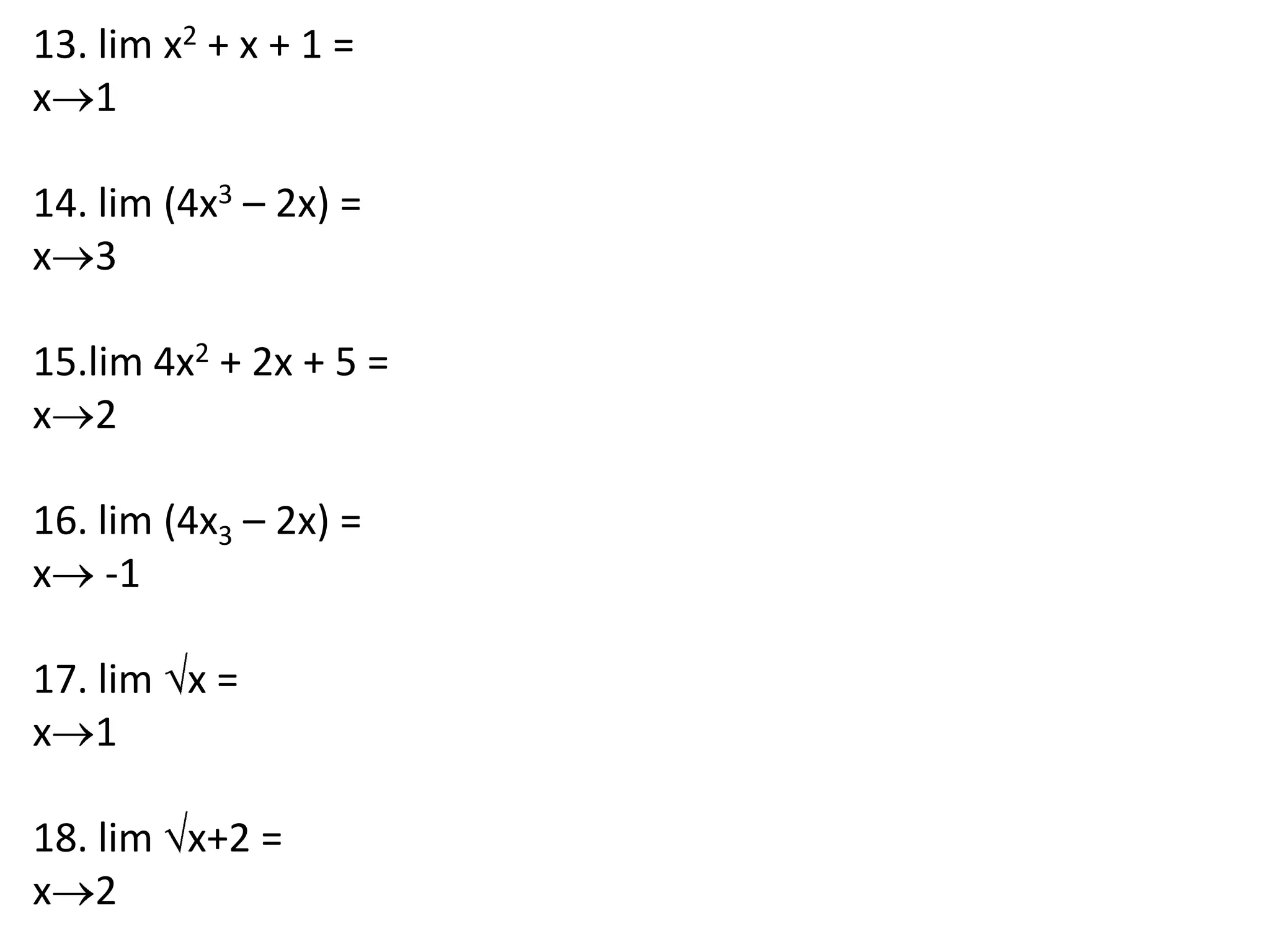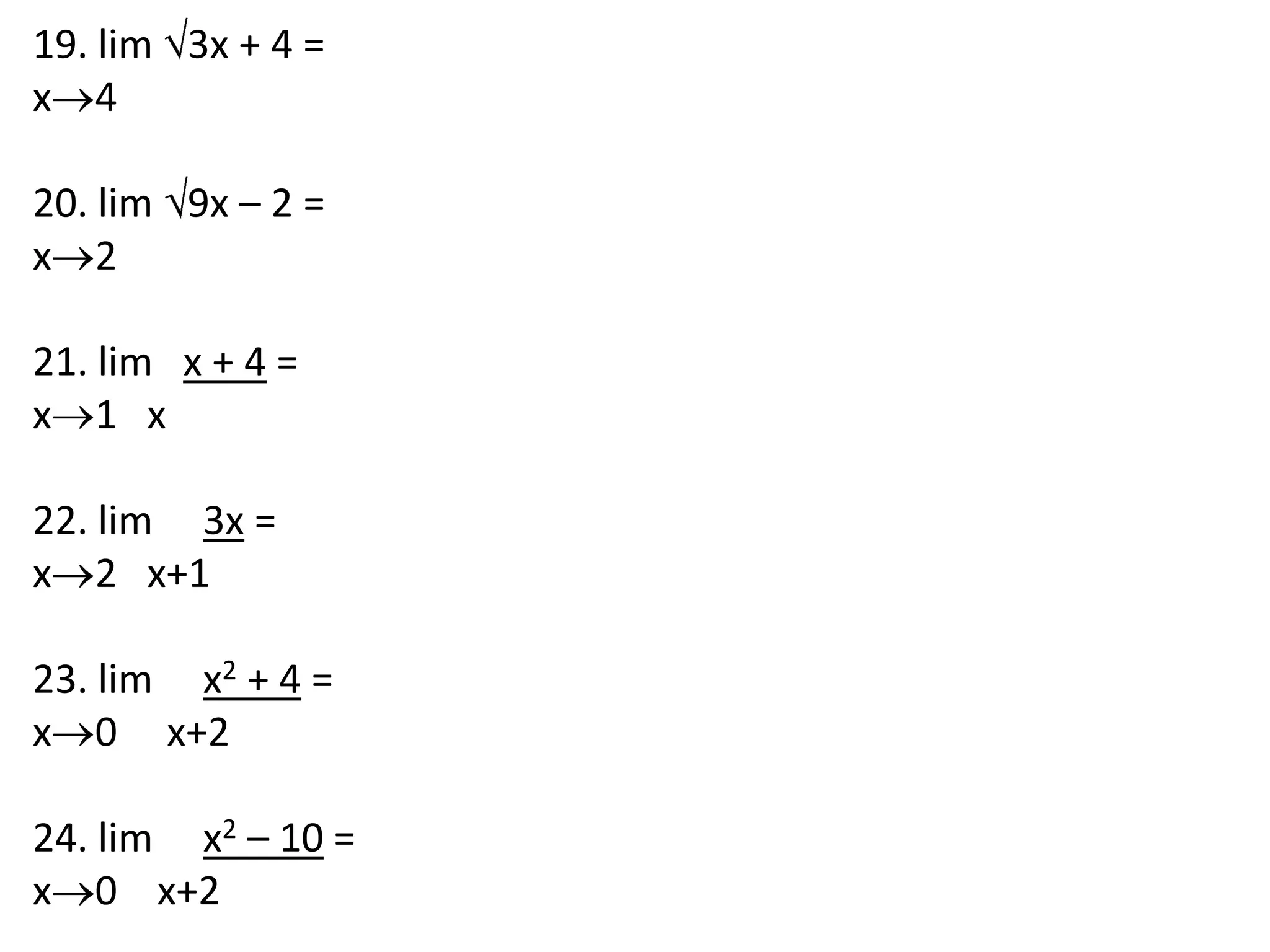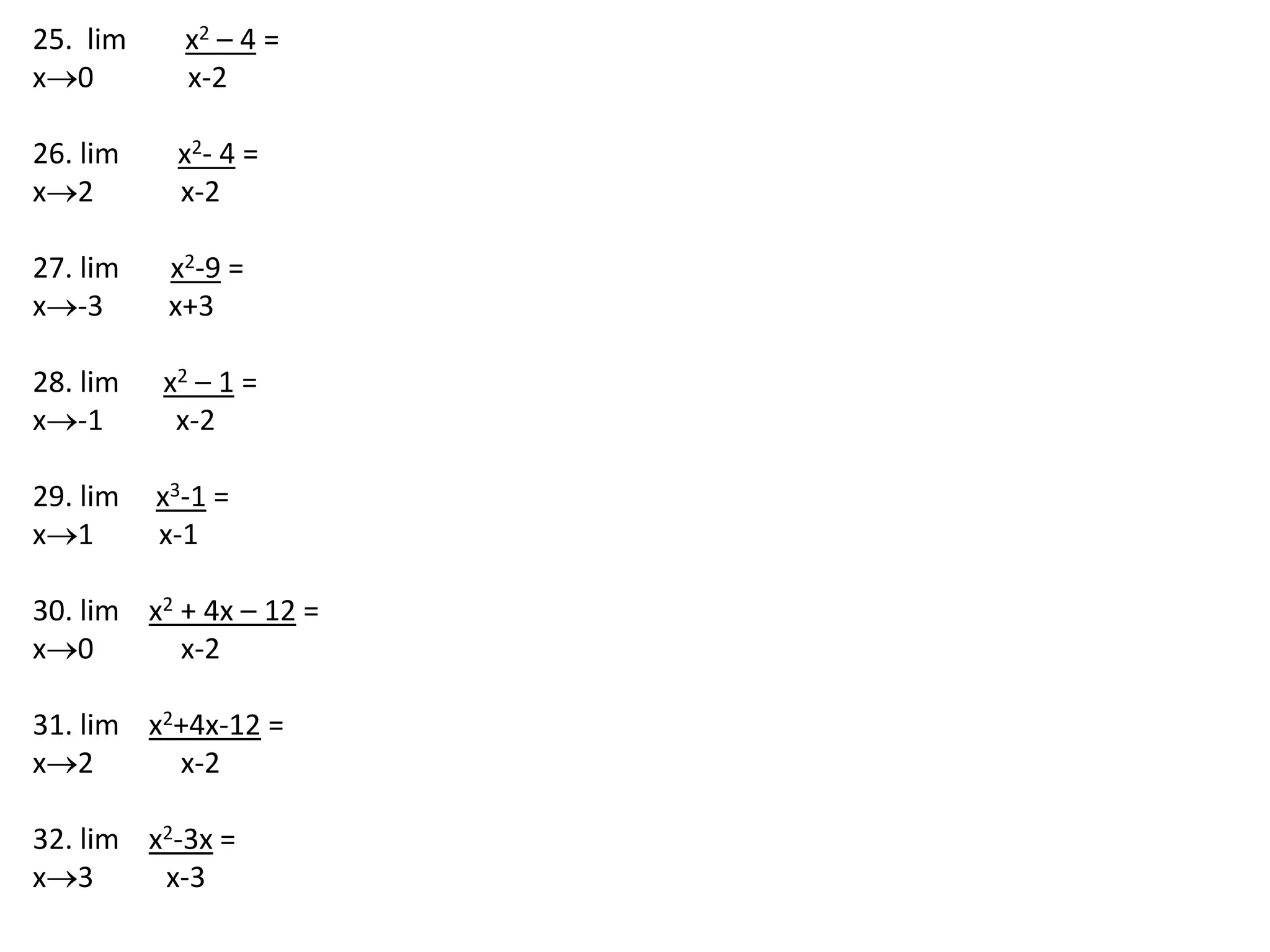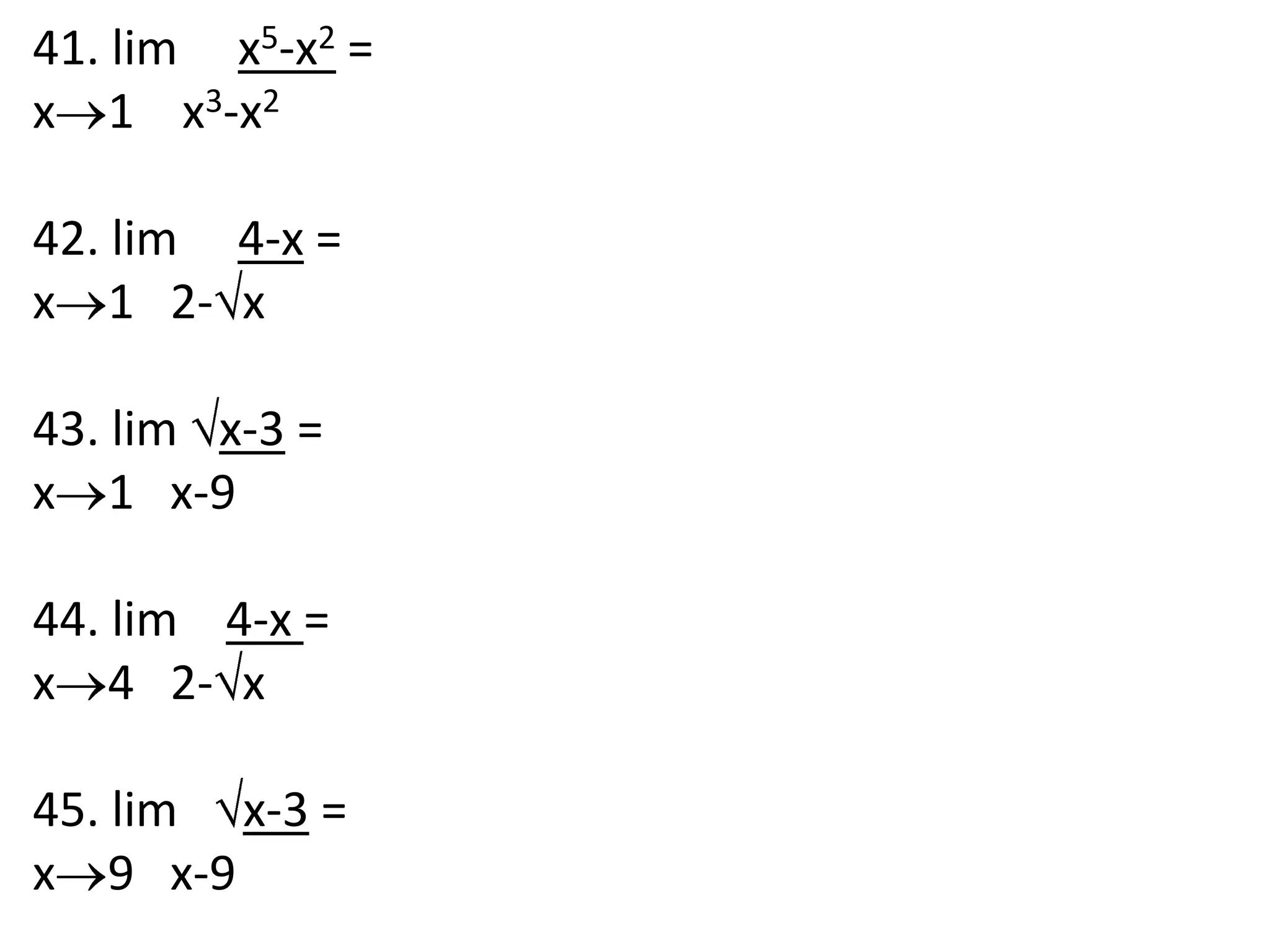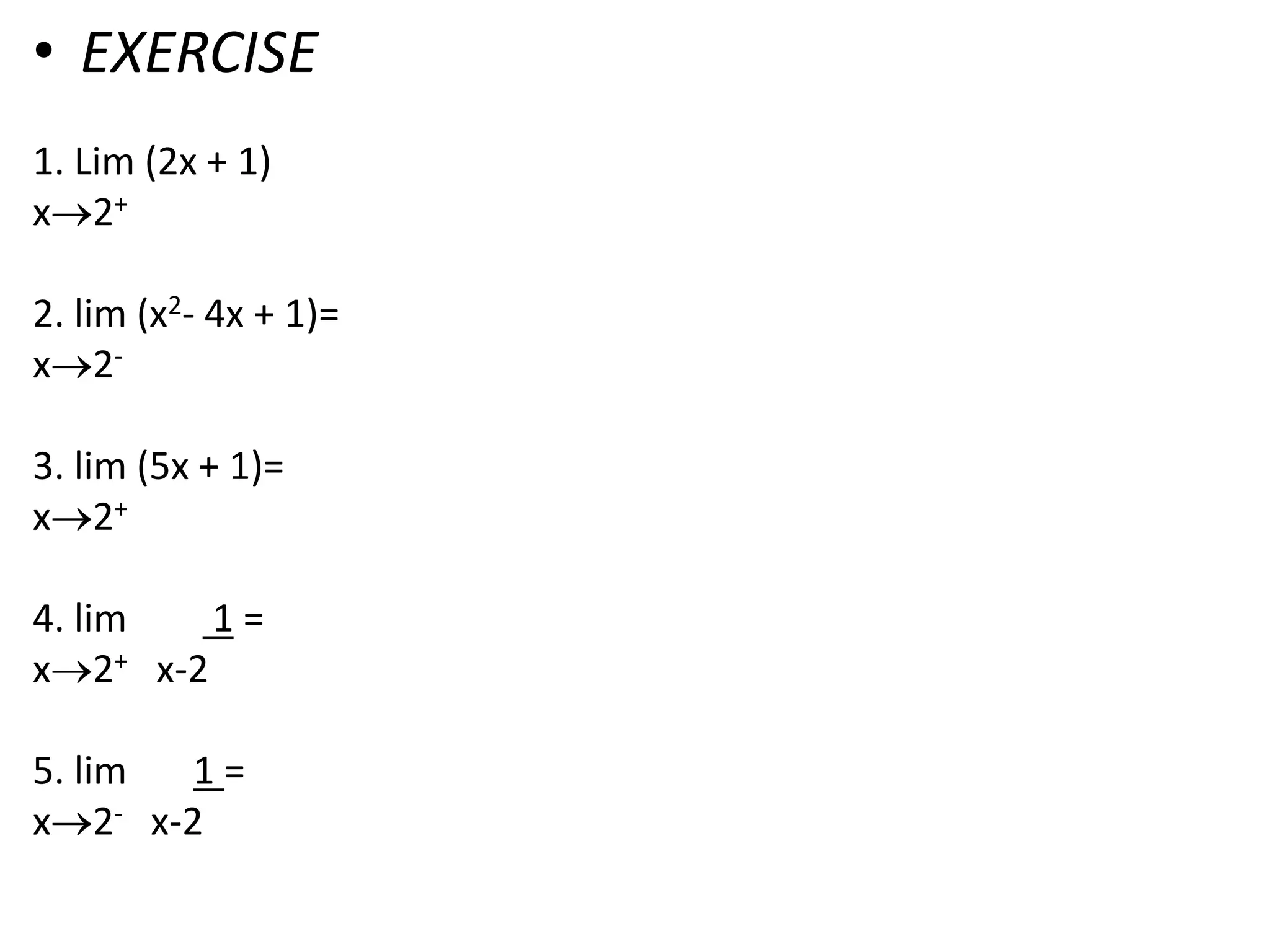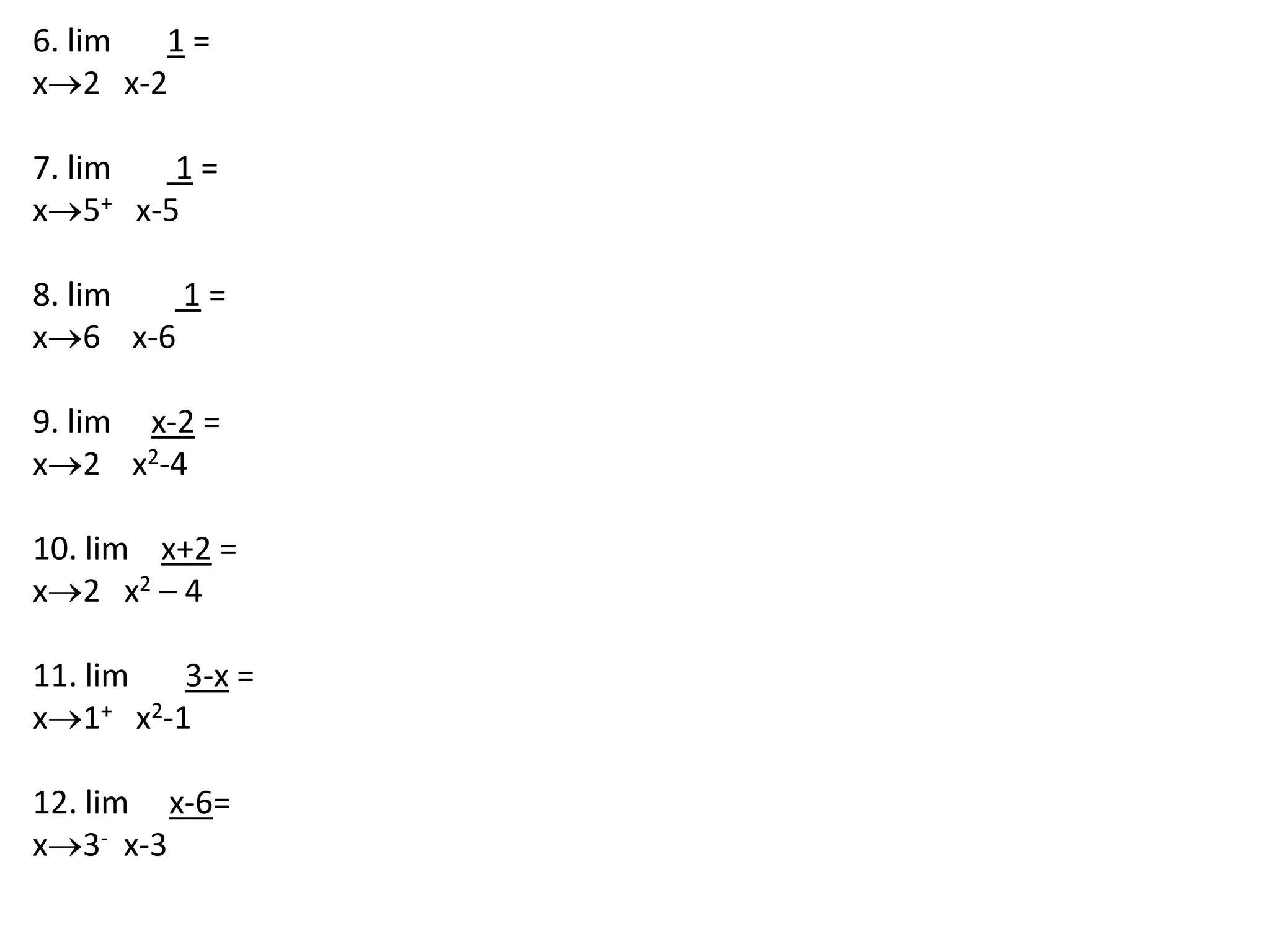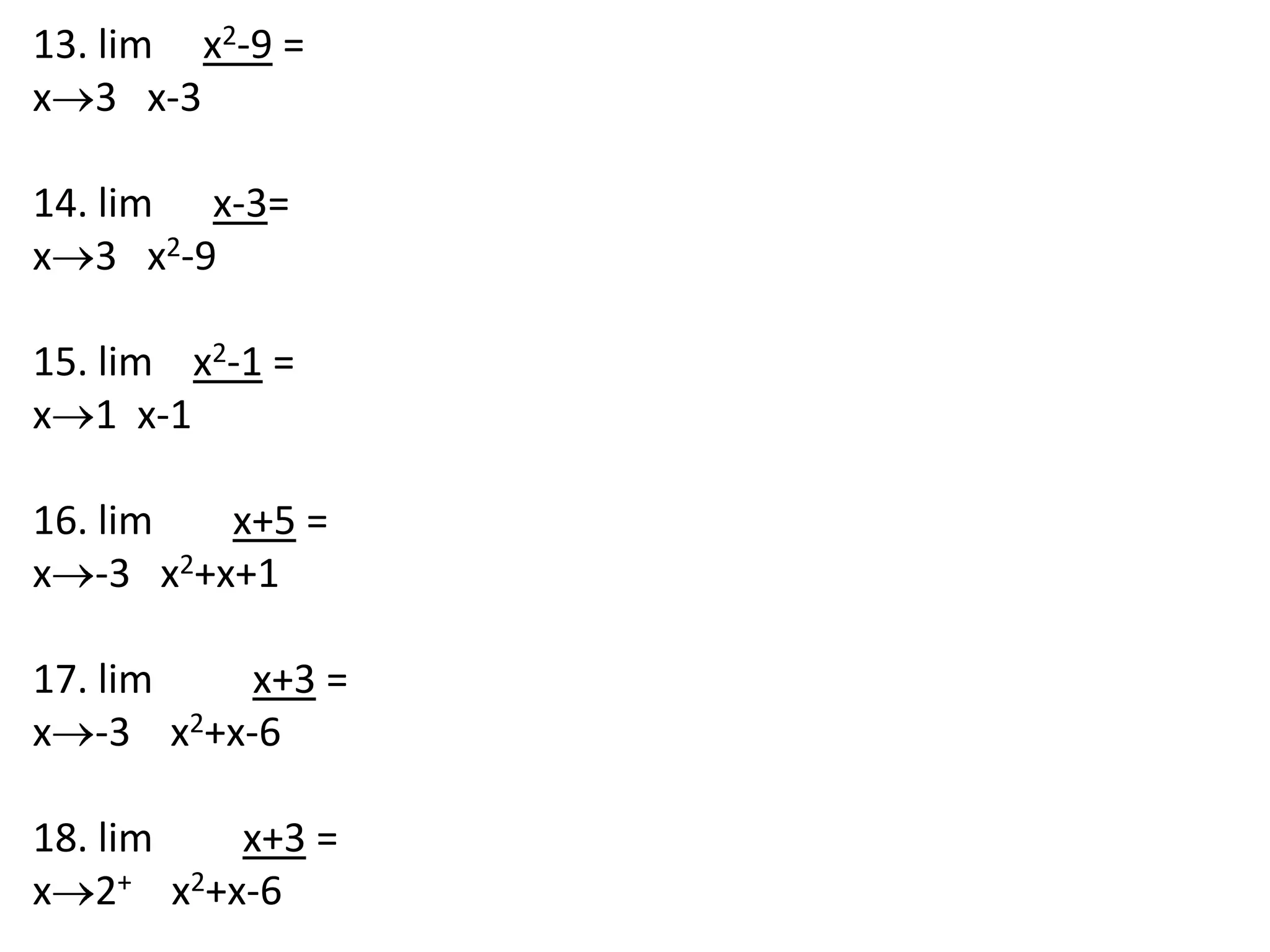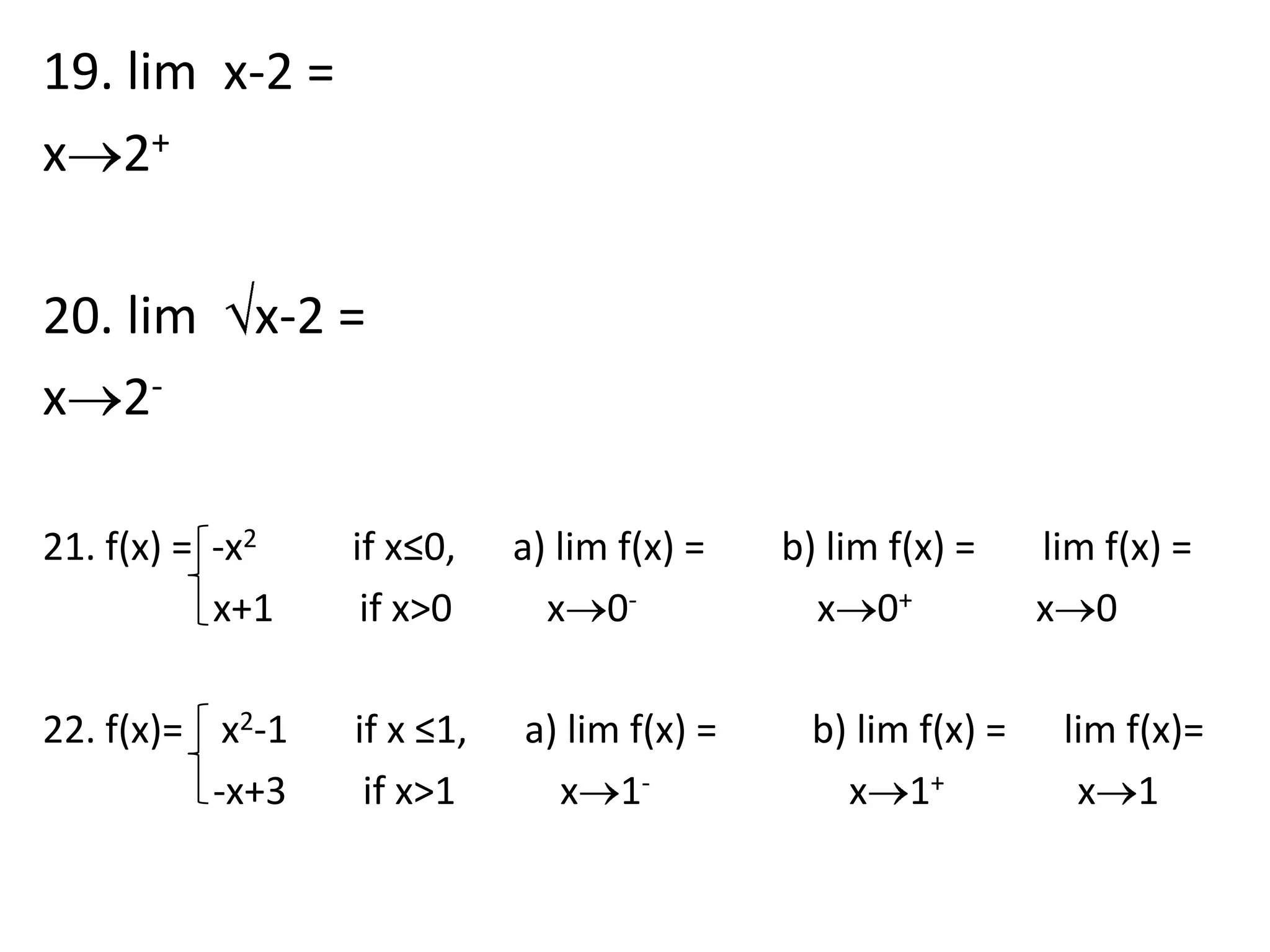This document discusses limits involving infinity. It defines an infinite limit as one where the function tends to positive or negative infinity as the variable approaches a value. An infinite limit is written as lim f(x) = +∞ if it tends to positive infinity, and lim f(x) = -∞ if it tends to negative infinity. As an example, the limit of the function f(x) = 1/(x-4)2 as x approaches 4 is written as lim f(x) = ∞, since the function grows without stopping as x gets closer to 4.

1. 2.6 THEOREMS OF LIMITS Given the functions f(x), g(x), the value “a” (the one that x approaches), and its limits: Lím f(x) = L lím g(x) = Mxaxa 1. For a constant f(x) = kLím k = kxa Example:Lím 3 = 3x2 2. For an independent variable f(x) = xLímx = axa Example:lím x=3x3

2. For a power f(x) = xn, with n = integerLim xn = anxa Example: Lím x2 = (3)2 = 9 x3 For a constant by a power f(x) = kxn, with n = integerLim kxn = k (lim xn) = k(an) Example:Lim kxn = k(lim xn) = k(an)xaxaExample:Lim 3x2 = 3 (lim x2) = 3(42) = 3 (16) = 48

3. For a sum of functionsLim [f(x) + g(x)] = lim f(x) + lim g(x) = L+Mxaxaxa example:lim [3x2 + 6x] = lim 3x2 + lim 6x = 12+ 12 = 24x2 x2x2 For a product of functionsLim [f(x)g(x) = [lim f(x)][lim g(x)] = (L)(M)xaxaxaExample:lim [(3x2)(6x)] = [lim 3x2][lim 6x] = (12)(12) = 144x2 x2x2For a quotient of functionsLim [f(x) ÷g(x)] = [lim f(x)]÷[lim g(x)] = (L) ÷ (M), if M0xaxaxa Example:lim [(3x2)2÷(6x)] = [lim 3x2]÷[lim 6x] = (12) ÷ (12) = 1x2 x2x2

4. For a function elevated to a powerLim [f(x)n = [lim f(x)]n = (L)n, with n = integer Example:Lim (3x2)2 = (lim 3x2)2 = [(3)(lim x2)2 = [(3)(22)2 = [12]2 = 144x2 x2x2 Lim [3x2 + 6x]2 = [lim 3x2 +6x]2 = [lim 3x2 + 6x]2 = [3 lim x2 + 6lim x]2= [3(2)2 + 6(2)]2 = [12+12]2 = [24]2 = 576 For a root of functionLim nf(x) = lim f(x) = L, with n= integer, f(x) ≥0xaxa Example:lim4x2 = lim 4x2 = 4(2)2 = 16 = 4x2 x2

5. EXERCISE1. Lim 5 =xa 2. Lim 4 =x0 3. Lim x=x3 4. lim x =x0 5. lim 2x =x3 6. lim 5x =x0

6. 7. lim x2 =x4 8. lim x3 =x2 9. lim 3x2 =x2 10. lim 4x2 =x-1 11. lim 3x2 + 2x =x1 12. lim (6x + 3)2 =x2

7. 13. lim x2 + x + 1 =x1 14. lim (4x3 – 2x) =x3 15.lim 4x2 + 2x + 5 =x2 16. lim (4x3 – 2x) =x -1 17. lim x =x1 18. lim x+2 =x2

8. 19. lim 3x + 4 =x4 20. lim 9x – 2 =x2 21. lim x + 4 =x1 x22. lim 3x =x2 x+1 23. lim x2 + 4 =x0 x+2 24. lim x2 – 10 =x0 x+2

9. 25. lim x2 – 4 =x0 x-2 26. lim x2- 4 =x2 x-2 27. lim x2-9 =x-3 x+3 28. lim x2 – 1 =x-1 x-2 29. lim x3-1 =x1 x-1 30. lim x2 + 4x – 12 =x0 x-2 31. lim x2+4x-12 = x2 x-2 32. lim x2-3x =x3 x-3

10. 33. lim x2-9 =x0 x2+2x-3 34. lim x2-3x =x3 x-3 35. lim x2-4 =x-2 x2+2x 36. lim x2-3x =x1 x 37. lim x2-3x =x0 x 38. lim 2x3 =x0 x6-x3 39. lim x4 – x2 =x0 x2 40. lim x5 – x2 =x0 x3 –x2

11. 41. lim x5-x2 =x1 x3-x2 42. lim 4-x =x1 2-x 43. lim x-3 =x1 x-9 44. lim 4-x =x4 2-x 45. lim x-3 =x9 x-9

12. 2.7 LATERAL LIMITIt is stated that the limit exist if the lateral limits are equals.The lateral limit is the value to which the function approaches when the variable “x” approaches to a value “a” either by its left side or by its right side.The following figures show the value “L” to which the function approaches when “x” approaches to a “a” either by a left of by the right.

13. LLaa“xa-”“xa+”

14. Notice how when the variable “x” approaches to “a”, the function approaches to “L”, and the graph shows that its points are approaching more each time to the position (a, L)The lateral limits are two: the lateral limit by the left and the lateral limit by the right.The lateral limit by the left is the value to which approaches the function when x approaches to a by the left.It is written: lim f(x) = L1xa- The lateral limit by the right is the value to which approaches the function when x approaches to a by the right.It is written: lim f(x) = L2xa+

15. The lateral limits, L1 and L2, are equal, then the limit of the function when x approaches to “a”, exists; instead, if they are different, it is said that the limit does not exists. If lim f(x) = lim f(x) = L, then lim f(x) =Lxa-xa+if lim f(x) ≠ lim f(x), then lim f(x) = does not existsxa- xa+ Example 1The following figure is the graph of f(x) = 0.1x3 – 0.5 x2 + 0.5x + 3.3. Observe the values to which the function approaches when the variable “x” approaches to 3. Notice that the lateral limits tend to a same value “L”.

16. You can see that when x approaches to 3 by the left, the limit is 3, and when x approaches to 3 by the right is also 3.Since when the variable “x” tends to 3, by both sides, the function tends to 3, then the limit is the function when x tend to 3 is 3.

17. EXAMPLE 2The following figure is the graph of the function in parts, f(x) = x2 -4x + 5, if x < 3 - 0.5x + 5, if x ≥3

18. Observe the values to which the function approaches when the variable “x” approaches to 3. Notice that the lateral limits tend to be different values.You can see that when x approaches to 3 by the left, the limit is 2, and when x approaches to 3 by the right the limit is 3.5.Since when the variable “x” tends to different values by both sides, then the limit of the function when x tends to 3, does not exists.

19. EXAMPLE 3Determine the following limit: lim 1 x4 x-4Solution:Two tables of values are elaborated; in one table it is given values to “x” that get closer to 4 by the left and in the other table, with values of “x” that get closer to 4 by the right. When solving the corresponding values of f(x) you will observe the value to which the function approaches.345

20. By the left4--∞By the right4+∞

21. As the variable x approaches to 4, the function tends to different values. In the first table it is observed that when x approaches to 4 by the left, the values of the function f(x) tends to -∞, and in the second table you see that when x approaches to 4 by the right, the values of the function f(x) tend to +∞.Therefore, lim 1 = does not exist x4 x-4

22. EXERCISE 1. Lim (2x + 1)x2+ 2. lim (x2- 4x + 1)=x2- 3. lim (5x + 1)=x2+ 4. lim 1 =x2+ x-2 5. lim 1 =x2- x-2

23. 6. lim 1 =x2 x-2 7. lim 1 =x5+ x-5 8. lim 1 =x6 x-6 9. lim x-2 =x2 x2-4 10. lim x+2 =x2 x2 – 4 11. lim 3-x =x1+ x2-1 12. lim x-6=x3- x-3

24. 13. lim x2-9 =x3 x-3 14. lim x-3=x3 x2-9 15. lim x2-1 =x1 x-1 16. lim x+5 =x-3 x2+x+1 17. lim x+3 =x-3 x2+x-6 18. lim x+3 =x2+ x2+x-6

25. 19. lim x-2 =x2+ 20. lim x-2 =x2- 21. f(x) = -x2 if x≤0, a) lim f(x) = b) lim f(x) = lim f(x) = x+1 if x>0 x0- x0+ x0 22. f(x)= x2-1 if x ≤1, a) lim f(x) = b) lim f(x) = lim f(x)= -x+3 if x>1 x1- x1+ x1

26. 23. F(x)= x2+3 if x≥1, a) lim f(x) = b) lim f(x)= lim f(x)= -x+3 if x>1 x1- x1+ x1 24. F(x)= x2-1 if x<1, a) lim f(x) = b) lim f(x)= lim f(x)= 1-x if x≥1 x1- x1+ x1 25. F(x)= 2 if x≤1, a) lim f(x) = b) lim f(x)= lim f(x)= -2 if x>1 x1- x1+ x1

27. Determine the indicated limit of the following graphs30. Graph of the function f(x) = x2- 4x + 5Lim f(x) = b) lim f(x)= c) lim f(x)= d) lim f(x)= e) lim f(x)= x0 x1 x2- + x x4

28. 31. Graph of the function f(x)= x2-2x+1 if<2 X2-6x+10 if x≥2a)lim f(x) = b) lim f(x) = c) lim f(x) = d) lim f(x) = e) lim f(x) = x0 x1 x 2- x 2+ x2

29. 32. Graph of the function f(x) = 0.5/(x-3)2.a)lim f(x) = b) lim f(x) = c) lim f(x) = d) lim f(x) = e) lim f(x) = x2 x2.5 x 3- x 3+ x4

30. 33. Based on the following figure, find the limit for each case.a)lim f(x) = b) lim f(x) = c) lim f(x) = d) lim f(x) = e) lim f(x) = x0 x4x 3+ x 3- x5

31. 2.8 LIMITS WHERE IS INVOLVED THE INFINITE2.8.1 Infinite Limit The infinite limit is the one where the function tends to infinite (positive of negative) when the variable tends to a value a. If the limit is +∞, it is written: lim f(x) = +∞. If the limit is -∞, it is written: lim f(x)= -∞ For example, in the graph f(x) = 1 (X-4)2

32. In the graph you can see that when x approaches to 4 by the left, the function tends to infinite, and in the same way occurs when approaching x to 4 by the right. This is, the function grows without stop. It is written:Lim 1 =∞x4 (x-4)2

33. Write the limit with the symbol of infinite does not mean that the limit exists, since there is no real value for “L”, it only symbolizes that the function grows (or decreases) with unbounded behavior.Sometimes just some of the lateral limits tend to infinite, or both tend to infinite, but one to plus infinite and the other to less infinite; growths or decreases with no stop, without border.

34. For example, the graph of f(x) = 1 (x-4)In the graph you can see that when x approaches to 4 by the left, the function tends to -∞, and when x tends to 4 by the right, the function tends to +∞. In this case, you write:Lim 1 = -∞x4 x-4 Lim 1 = +∞x4 x-4

35. However, since the lateral limits are different you write lim1 = does not exist x4 x-4 to evaluate this class of limits, it is convenient to use the approximation method or to use the graph of the function. Observe that these classes of limits represent graphically a vertical asymptote.

36. 2.8.2 Limits in the infiniteThe limit in the infinite is the one where the variable tends to infinite (positive or negative) and the function tends to a value L. If x tends to +∞, it is written: lim f(x) = L. if x tends to -∞, it is written: lim = f(x) = L. x+∞ x-∞ The limit of algebraic function (polynomial) when x tends to infinite does not exists, since the function also tends to infinite positive or negative.For example, in the limit of the function f(x) = x+2, when x tends to infinite:Lim (x+2)x+∞ The solution is:lim (x+2) = (∞+2)= ∞x+∞

37. The limit of a rational function can be zero; a value different from zero or well does not exists.In this class of limits, it is started with the fact that the limit of an expression where a constant is divided between a value that tends to the infinite, the result tends to zero. Lim k = 0x∞ xn To evaluate this class of limits, where x tends to infinite, the method of approximate can be used, using the graph of the function, or well to transform the expression dividing it between the bases of greater exponent of the denominator in such a way that the previous limit can be applied.

38. EXAMPLE 1Determine the limit of the function f(x) = (6x – 2)/(3x+3), when x tends to infinite. Lim 6x-2x+∞ 3x+3 Solution by approximation:We have that when x tends to a +∞, the function tends to 2.

39. b) Solution using the graphIn the graph you can see that when x tends to +∞, the function tends to 2.

40. c) Solution taking as referenceLim k =0x∞ xn Each one of the terms of the expression is divided between the variable with greater exponent of the denominator (for this case it is divided between x): lim6x-2 = lim6x/x – 2/xx+∞ 3x+3 x+∞ 3x/x + 3/x It is simplified: lim6 – 2/xx+∞ 3 + 3/x

41. It is applied the limit of reference: lim6 – 2/x = 6-0 = 6 = 2x+∞ 3 + 3/x 3+0 3 So lim6x – 2 = 2x+∞ 3x + 3