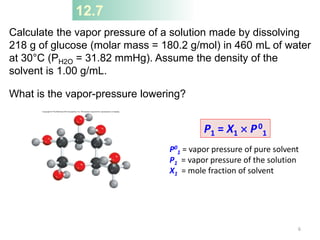
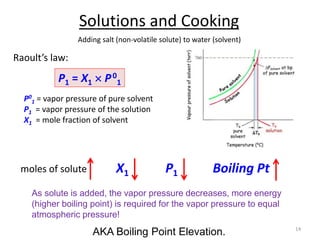
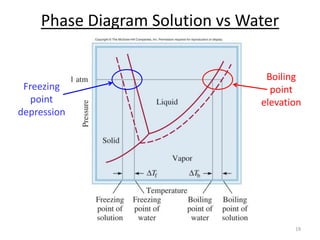
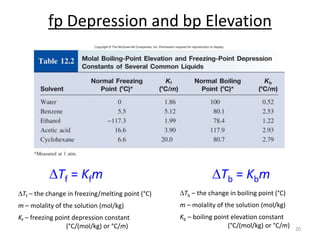
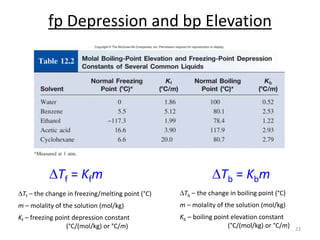
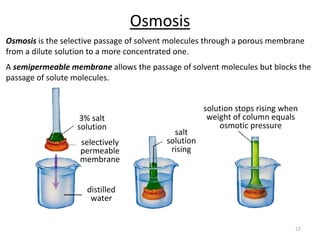
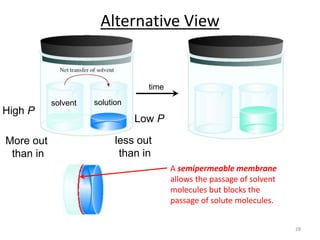
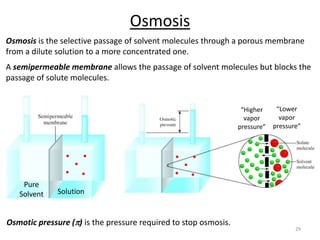
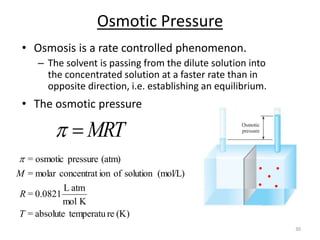
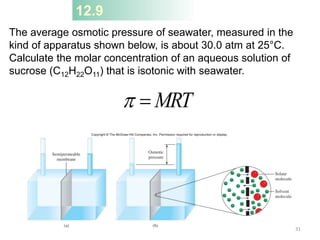
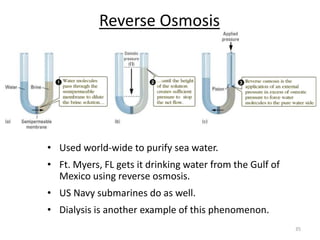
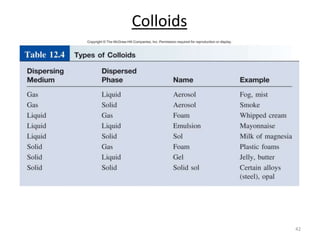
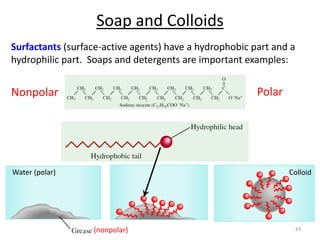
This document discusses colligative properties of solutions, which are properties that depend only on the number of solute particles in solution. It defines four main colligative properties - vapor pressure lowering, boiling point elevation, freezing point depression, and osmotic pressure. The document provides formulas for calculating these properties and includes examples of their application. It also discusses how colligative properties are affected in electrolyte vs. nonelectrolyte solutions and introduces the concept of van't Hoff factor. Finally, it briefly touches on colloids and their differences from true solutions.