Dokumen ini membahas konsep dasar logika proposisi, termasuk hukum-hukum logika, tabel kebenaran, dan jenis proposisi seperti tautologi dan kontradiksi. Juga dijelaskan tentang proposisi bersyarat, bi-kondisional, dan tugas-tugas terkait penerapan konsep logika dalam bentuk simbolik. Di akhir, terdapat daftar pustaka yang merujuk pada buku tentang matematika diskrit.

1. MATEMATIKA
DISKRIT
LOGIKA
(PROPOSISI)

2. Sub Topik
• Hukum-hukum Logika Proposisi
• Proposisi Bersyarat
• Varian proposisi bersyarat
• Bi-Implikasi

3. Tujuan Pembelajaran
Memahami konsep proposisi
Memahami konsep kombinasi proposisi
Memahami penggunaan tabel kebenaran
Memahami hukum - hukum logika proposisi

4. HUKUM PROPOSISIONAL P, Q,DAN R
1.Hukum de Morgan : (PQ)  (PQ)
2.Hukum de Morgan : (PQ)  (PQ)
3.Hukum distributif : P(QR)  (PQ)  (PR)
P(QR)  (PQ) (PR)
4.Hukum komutatif : (PQ)  (QP)
(PQ)  (QP)
5.Hukum asosiatif : ((PQ) R)  (P (QR))
((PQ) R)  (P (QR))
6.Hukum kontrapositif : (PQ)  ( Q P)

5. 5
Dua buah proposisi, P(p, q, ..) dan Q(p, q, ..) disebut
ekivalen secara logika jika keduanya mempunyai tabel
kebenaran yang identik.
Notasi: P(p, q, …)  Q(p, q, …)
Hukum De Morgan: ~(p  q)  ~p  ~q.
p q p  q ~ (p  q) ~ p ~q ~ p  ~ q
T T T F F F F
T F F T F T T
F T F T T F T
F F F T T T T

6. Contoh Soal 1
• Jika p, q dan r adalah proposisi maka carilah
tabel kebenaran dari :
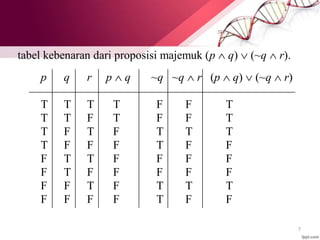
1. (p  q) V (q  r)
2. (p  q) V r
3. (p V q)  r
4. [(p V q)  r] V [(p  r) V (q  p)]

7. 7
tabel kebenaran dari proposisi majemuk (p  q)  (~q  r).
p q r p  q ~q ~q  r (p  q)  (~q  r)
T T T T F F T
T T F T F F T
T F T F T T T
T F F F T F F
F T T F F F F
F T F F F F F
F F T F T T T
F F F F T F F

8. 8
• Proposisi disebut tautologi jika ia benar untuk
semua kasus
• Proposisi disebut kontradiksi jika ia salah untuk
semua kasus.

9. 9
p  ~(p  q) adalah sebuah tautologi
p q p  q ~(p  q) p  ~(p  q)
T T T F T
T F F T T
F T F T T
F F F T T

10. 10
(p  q)  ~(p  q) adalah sebuah kontradiksi
p q p  q p  q ~(p  q) (p  q)  ~(p  q)
T T T F F F
T F F T F F
F T F T F F
F F F F T F

11. 11
Disjungsi EksklusifKata “atau” (or) dalam operasi logika digunakan dalam salah
satu dari dua cara:
1. Inclusive or
“atau” berarti “p atau q atau keduanya”
Contoh: “Tenaga IT yang dibutuhkan menguasai Bahasa
C++ atau Java”.
2. Exclusive or
“atau” berarti “p atau q tetapi bukan keduanya”.
Contoh: “Ia dihukum 5 tahun atau denda 10 juta”.

12. 12
Operator logika disjungsi eksklusif: xor
Notasi: 
Tabel kebenaran:
p q p  q
T T F
T F T
F T T
F F F

13. Proposisi Bersyarat (Implikasi)
• Misalkan p dan q adalah proposisi.
• Notasi dari proposisi majemuk “jika p maka q” :
p  q
• Proposisi p disebut hipotesis (antesenden atau premis
atau kondisi)
• Proposisi q disebut konklusi (konsekuen)
• Implikasi p  q hanya salah jika p benar tetapi q salah,
selain itu implikasi benilai benar
p q p  q
T T T
T F F
F T T
F F T
T = True (benar)
F = False (salah)

14. • Konsep matematik mengenai implikasi
independen dari hubungan sebab-akibat antara
hipotesis dan konklusi
• Ekspresi lain dari implikasi p  q :
a)Jika p maka q : if p then q
b)Jika p, q : if p, q
c) p mengakibatkan q : p implies q
d)q jika p : q if p
e)p hanya jika q : p only if q
f) p syarat cukup agar q :p is sufficient for p
g)q syarat perlu bagi p :q is necessary for p
h)q bilamana p : q whenever p
Proposisi Bersyarat (Implikasi)

15. Contoh Kalimat implikasi
a) Jika hari hujan maka tanaman akan tumbuh subur
b) Jika tekanan gas diperbesar, mobil melaju kencang
c) Es yang mencair di kutub mengakibatkan permukaan
air laut naik
d) Orang itu mau berangkat jika ia diberi ongkos jalan
e) Hani bisa mengambil MK Struktur Data hanya jika ia
sudah lulus MK Algoritma Pemrograman
f) Percikan api dari rokok adalah Syarat cukup agar pom
bensin meledak
g) mengontrak pemain asing kenamaan adalah Syarat perlu
bagi Indonesia agar ikut Piala Dunia
h) Banjir bandang terjadi bilamana hutan ditebangi

16. Pengubahan menjadi bentuk
proposisi jika p maka q
a) Jika hari hujan maka tanaman akan tumbuh subur
b) Jika tekanan gas diperbesar, maka mobil melaju
kencang
c) Jika Es yang mencair di kutub, maka permukaan air laut
naik
d) Jika Orang itu diberi ongkos jalan, maka ia mau
berangkat
e) Jika Hani sudah lulus MK Algoritma Pemrograman,
maka ia bisa mengambil MK Struktur Data
f) Jika api memercik dari rokok, maka pom bensin
meledak
g) Jika Indonesia ikut Piala Dunia, maka Indonesia
mengontrak pemain asing kenamaan
h) Jika Hutan ditebangi, maka Banjir bandang terjadi

17. Varian Proposisi Bersyarat
• Konvers (kebalikan)
Notasi : q p
• Invers
Notasi : p  q
• Kontraposisi :
Notasi : q  p
p q p q Implikasi
pq
Konvers
qp
Invers
p q
Kontraposisi
q p
T T F F T T T T
T F F T F T T F
F T T F T F F T
F F T T T T T T

18. Contoh Soal 2
• Jika Fani rajin belajar, maka ia mendapat nilai bagus
Sehingga ...
Konvers :
Invers :
Kontraposisi :

19. Bi-kondisional (Bi-implikasi)
• Misalkan p dan q adalah proposisi.
• Proposisi majemuk “p jika dan hanya jika q “ dinyatakan
dengan notasi :
p  q
• Penyataan p  q bernilai benar bila p dan q mempunyai
nilai kebenaran yang sama
p q p  q
T T T
T F F
F T F
F F T
T = True (benar)
F = False (salah)

20. • Bi-kondisional pq ekivalen dengan (p  q)  (q  p)
• Bi-kondisional dapat dinyatakan dengan kata-kata :
– p jika hanya jika q
– p adalah syarat perlu dan cukup untuk q
– Jika p maka q, dan sebaliknya
– P iff q
p q p q pq qp (p  q)  (q  p)
T T T T T T
T F F F T F
F T F T F F
F F T T T T

21. Contoh proposisi majemuk dari bi-implikasi
a) 1 + 1 = 2 jika hanya jika 2 + 2 = 4
b) Syarat cukup dan syarat perlu agar hari hujan
adalah kelembaban udara tinggi
c) Jika budi orang kaya maka budi mempunyai banyak
uang, dan sebaliknya
d) Surabaya terletak di Jawa Timur iff Jawa Timur
adalah sebuah propinsi di Indonesia

22. VIDEO PEMBELAJARAN

23. TUGAS
1. Misalkan p adalah “Ani bisa berbahasa Madura”, q adalah “ Ani
bisa berbahasa Indonesia”, dan r adalah “ Ani bisa berbahasa
Inggris”. Terjemahkan kalimat majemuk berikut ke dalam notasi
simbolik :
a. Ani bisa berbahasa Madura atau Indonesia
b. Ani bisa berbahasa Indonesia tetapi tidak bahasa Inggris.
c. Ani bisa berbahasa Madura atau bahasa Indonesia, atau dia tidak
bisa berbahasa Inggris atau bahasa Indonesia.
d. Tidak benar bahwa Ani bisa berbahasa Indonesia atau Inggris
e. Tidak benar bahwa Ani bisa berbahasa Indonesia atau Inggris
tetapi tidak bahasa Madura
f. Tidak benar bahwa Ani tidak bisa berbahasa Madura, Indonesia,
maupun Inggris.

24. TUGAS
2. Tuliskan tabel kebenaran untuk setiap proposisi
berikut :
a. (p ᴠ q) ᴧ ̴p
b. ̴(p ᴧ q) ᴠ ( ̴q v r)
c. ( ̴p v ̴q ) v p
d. (p v q) → ̴q
e. ( ̴q  p)  (p  ̴q)

25. TUGAS
3. Misalkan p adalah “ Hari ini adalah hari senin”, q
adalah “Hujan turun”, dan r adalah “Hari ini panas”.
Terjemahkan notasi simbolik ini dengan kata-kata.
a. p ᴠ q
b. ̴p ᴧ (q ᴠ r)
c. ̴ (p ᴠ q) ᴧ r
d. (p ᴧ q) ᴧ ̴(r ᴠ p)
e. ̴ q  ̴p

26. Daftar Pustaka
• Rinaldi Munir, 2005, “Matematika diskrit”,
INFORMATIKA Bandung