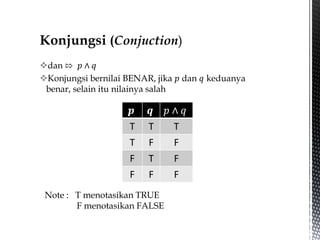
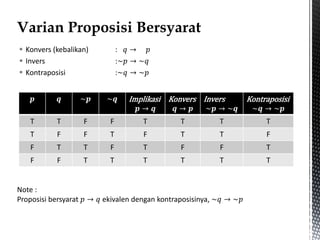
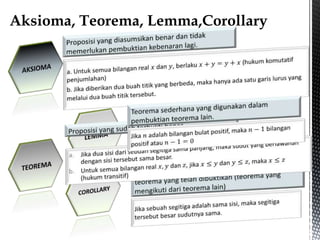
Dokumen ini adalah materi kuliah tentang logika proposisi dalam matematika diskrit, yang mencakup definisi proposisi, hukum-hukum logika, serta operator logika seperti konjungsi, disjungsi, dan negasi. Materi juga membahas proposisi bersyarat, bikondisional, dan metode inferensi dalam logika. Selain itu, terdapat contoh dan penjelasan mengenai tabel kebenaran dan ekivalensi logika.

1. Pengajar :
Heni Widayani, M.Si
Mata Kuliah :Matematika Diskrit
REVIEW
MATHEMATICAL
REASONING
Senin, 26 Januari 2018

2. Mereview materi logika (Kalkulus Proposisi)
Mereview kombinasi proposisi
Mereview Hukum-hukum logika proposisi
Mengecek kebenaran suatu proposisi atau kesahihan suatu argumen

3. Proposisi adalah kalimat deklaratif yang bernilai benar (true) atau
salah (false), tetapi tidak sekaligus keduanya. Kebenaran atau
kesalahan dari sebuah kalimat disebut nilai kebenarannya (Truth
value).
Proposisi dilambangkan dengan huruf kecil, seperti 𝑝, 𝑞, 𝑟, …
Cara mendefinisikan proposisi
𝑝 ∶ UIN Maulana Malik Ibrahim berada di kota Malang
𝑞 ∶ Jurusan Matematika UIN Malang berada di Gedung
Bacharudin Jusuf Habibie.
Bidang logika yang membahas proposisi dinamakan kalkulus
proporsi (Propositional calculus) atau logika proposisi
(Propositional logic)

4. 1. Soekarno adalah Presiden pertama Republik Indonesia.
2. 6 adalah bilangan genap
3. 12 ≥ 19
4. Ibukota Provinsi Jawa Timur adalah Malang.
5. Jam berapa kereta Penataran tiba di Malang?
6. Serahkan uangmu sekarang!
7. 𝑥 > 3
8. 𝑥 + 3 = 8
9. Untuk sembarang bilangan bulat 𝑛 ≥ 0, maka 2𝑛 adalah
bilangan genap.
10.Untuk setiap 𝑥 dan 𝑦 anggota himpunan bilangan riil,
berlaku 𝑦 + 𝑥 = 𝑥 + 𝑦
P T
P T
P F
P F
BP
BP
BP
BP
P T
P T

5. Operator Biner : membutuhkan minimal dua proposisi
1. dan (and)
2. atau (or)
Operator Uner : membutuhkan satu buah proposisi (tidak (not))
Proposisi baru yang diperoleh dari pengkombinasian beberapa proposisi
disebut majemuk (compound proposition).
Sedangkan proposisi yang bukan merupakan kombinasi proposisi lain
disebut proposisi atomik.

6. George Boole (1854, The Laws of Thought) mendefinisikan 3 macam
proposisi majemuk sebagai berikut
Misalkan 𝑝 dan 𝑞 adalah proposisi.
1. Konjungsi (conjuction) ⇰ dan ⇰ 𝒑 ∧ 𝒒
2. Disjungsi (disjunction) inklusif ⇰ atau ⇰ 𝒑 ∨ 𝒒
3. Disjungsi ekslusif ⇰ atau tetapi bukan keduanya ⇰𝒑⨁𝒒
4. Ingkaran (negation) ⇰ tidak 𝑝 ⇰ ~𝒑, ¬𝑝, 𝑝 , 𝑛𝑜𝑡 𝑝

7. dan ⇰ 𝑝 ∧ 𝑞
Konjungsi bernilai BENAR, jika 𝑝 dan 𝑞 keduanya
benar, selain itu nilainya salah
𝒑 𝒒 𝑝 ∧ 𝑞
T T T
T F F
F T F
F F F
Note : T menotasikan TRUE
F menotasikan FALSE

8. atau => 𝑝 ∨ 𝑞
Disjungsi bernilai SALAH jika 𝑝 dan 𝑞 keduanya salah, selain itu
nilainya benar.
“Tenaga IT yang dibutuhkan harus menguasai Bahasa C++ atau Java”
Artinya :
Tenaga It yang diterima harus menguasai salah satu dari bahasa
Java atau Bahasa C++ atau kedua-duanya.
𝒑 𝒒 𝒑 ∨ 𝒒
T T T
T F T
F T T
F F F

9. 𝑝 atau 𝑞 tetapi bukan keduanya => 𝒑⨁𝒒
Proposisi yang bernilai benar bila hanya salah satu dari 𝑝 dan
𝑞 benar, selain itu nilainya salah.
Pada sebuah ajangan perlombaan, pemenang dijanjikan mendapat hadiah.
Hadiahnya adalah sebuah pesawat televisi 20 inchi. Jika pemenang tidak
menginginkan membawa TV, panitia menggantinya dengan uang sebesar
harga TV tersebut.
“Pemenang lomba mendapat hadiah berupa TV atau uang”
𝒑 𝒒 𝒑⨁𝒒
T T F
T F T
F T T
F F F

10. 1. Ingkaran (negation) => tidak/bukan 𝑝 => ~𝒑, ¬𝑝, 𝑝 , 𝑛𝑜𝑡 𝑝
2. Negasi 𝑝, bernilai benar jika 𝑝 salah, sebaliknya bernilai salah jika 𝑝 benar.
𝒑 ~𝒑
T F
F T

11. Proposisi bersyarat (Implikasi)
 Misalkan 𝑝 dan 𝑞 adalah proposisi. Proposisi majemuk “jika 𝑝 maka 𝑞” disebut
proposisi bersyarat (implikasi) dan dilambangkan dengan 𝑝 ⟶ 𝑞. Proposisi 𝑝
disebut hipotesis (premis, kondisi antesenden) dan proposisi 𝑞 disebut konklusi
(konsekuen).
 Implikasi 𝑝 ⟶ 𝑞 hanya salah jika 𝑝 benar tetapi 𝑞 salah, selain itu implikasi bernilai
benar.
𝒑 𝒒 𝒑 → 𝒒
T T T
T F F
F T T
F F T
 Implikasi 𝑝 → 𝑞 ekuivalen secara logika dengan ~𝑝 ∨ 𝑞
Cara menyatakan implikasi 𝑝 → 𝑞
a. Jika 𝑝 maka 𝑞 (if 𝑝, then 𝑞)
b. Jika 𝑝, 𝑞 (if 𝑝, 𝑞)
c. 𝑝 mengakibatkan 𝑞 (𝑝 implies 𝑞)
d. 𝑞 jika 𝑝 (𝑞 if 𝑝)
e. 𝑝 hanya jika 𝑞 (𝑝 only if 𝑞)
f. 𝑝 syarat cukup agar 𝑞 (𝑝 is sufficient for 𝑞)
g. 𝑞 syarat perlu bagi 𝑝 (𝑞 is necessary for 𝑝)
h. 𝑞 bilamana 𝑝 (𝑞 whenever 𝑝)

12. “Jika nilai ujian akhir Anda 80 atau lebih, maka anda akan mendapat nilai A untuk
kuliah ini.”
Kasus 1 :
Nilai ujian akhir Anda di atas 80 (hipotesis BENAR) dan anda mendapat nilai A untuk
kuliah tersebut (konklusi BENAR). Pada kasus ini, pernyataan dosen Anda BENAR
Kasus 2 :
Nilai ujian akhir Anda di atas 80( hipotesis BENAR) tetapi Anda tidak mendapat nilai A
(konklusi SALAH). Pada kasus ini, dosen Anda berbohong (Pernyataan SALAH)
Kasus 3 :
Nilai ujian akhir Anda di bawah 80 (hipotesis SALAH) dan Anda mendapat nilai A
(konklusi BENAR). Pada kasus ini dosen anda tidak dapat dikatakan salah (Mungkin ia
melihat kemampuan Anda secara rata-rata bagus sehingga ia tidak ragu memberi nilai
A) (Pernyataan BENAR)
Kasus 4 :
Nilai ujian akhir Anda di bawah 80 (hipotesis SALAH) dan anda tidak mendapat nilai A
(konklusi SALAH). Pada kasus ini dosen anda BENAR.

13. Jika paris adalah ibukota Perancis, maka 1+1=2.

14.  Konvers (kebalikan) : 𝑞 → 𝑝
 Invers :~𝑝 → ~𝑞
 Kontraposisi :~𝑞 → ~𝑝
𝒑 𝒒 ~𝒑 ~𝒒 Implikasi
𝒑 → 𝒒
Konvers
𝒒 → 𝒑
Invers
~𝒑 → ~𝒒
Kontraposisi
~𝒒 → ~𝒑
T T F F T T T T
T F F T F T T F
F T T F T F F T
F F T T T T T T
Note :
Proposisi bersyarat 𝑝 → 𝑞 ekivalen dengan kontraposisinya, ~𝑞 → ~𝑝

15.  Proposisi majemuk “𝑝 jika dan hanya jika 𝑞” disebut bikondisional (bi-implikasi) dan
dilambangkan dengan 𝑝 ↔ 𝑞.
 Pernyataan 𝑝 ↔ 𝑞 adalah BENAR jika 𝑝 dan 𝑞 mempunyai nilai kebenaran yang
sama, yakni jika 𝑝 dan 𝑞 keduanya benar atau 𝑝 dan 𝑞 keduanya salah.
𝒑 𝒒 𝒑 ↔ 𝒒
T T T
T F F
F T F
F F T
 Pernyataan 𝑝 ↔ 𝑞 ekivalen secara logika dengan (𝑝 → 𝑞) ∧ 𝑞 → 𝑝
Cara menyatakan bikondisional 𝑝 ↔ 𝑞
a. 𝑝 jika dan hanya jika 𝑞 (𝑝 if and only if 𝑞)
b. 𝑝 adalah syarat perlu dan cukup untuk 𝑞 (𝑝 is necessary and sufficient for 𝑞)
c. Jika 𝑝 maka 𝑞, dan sebaliknya (if 𝑝 then 𝑞, and conversely)
d. 𝑝 iff 𝑞

16. Proses penarikan kesimpulan dari beberapa proposisi disebut inferensi.
 Modus Ponen (law of detachment) ⇰ 𝑝 ⟶ 𝑞 ∧ 𝑞 → 𝑞
 Modus Tollen ⇰ 𝑝 ⟶ 𝑞 ∧ ~𝑞 → ~𝑝
 Silogisme Hipotetis ⇰ 𝑝 → 𝑞 ∧ 𝑞 → 𝑟 → 𝑝 ⟶ 𝑟
 Silogisme Disjungtif ⇰ 𝑝 ∨ 𝑞 ∧∼ 𝑝 → 𝑞
 Simplifikasi ⇰ 𝑝 ∧ 𝑞 → 𝑝
 Penjumlahan ⇰ 𝑝 ⟶ 𝑝 ∨ 𝑞
 Konjungsi ⇰ 𝑝 ∧ 𝑞 → 𝑝 ∧ 𝑞

17. Jika 𝑝, 𝑞, dan 𝑟 adalah proposisi. Bentuklah tabel kebenaran dari ekspresi logika
1. 𝑝 ∧ 𝑞 ∨ ∼ 𝑞 ∧ 𝑟 T T T F F F T F
2. 𝑝 ∨∼ 𝑝 ∧ 𝑞 T T T T
3. 𝑝 ∧ 𝑞 ∧∼ 𝑝 ∨ 𝑞 F F F F
4. ∼ 𝑝 ∧ 𝑞 F T T T
5. ∼ 𝑝 ∨∼ 𝑞 F T T T
6. ~𝑝 → 𝑝 → 𝑞
7. ~ 𝑝 → 𝑞 → ~𝑞
8. 𝑝 ∧ 𝑞 → 𝑝 → 𝑞
9. 𝑝 ∨ 𝑞 ∧∼ 𝑝
10. ∼ 𝑞 → 𝑝 → 𝑝 → ~𝑞
Noted :
 Sebuah proposisi majemuk disebut TAUTOLOGI jika ia benar untuk semua kasus.
 Sebaliknya disebut KONTRADIKSI jika salah untuk semua kasus.
 Dua buah proposisi majemuk, P(𝑝, 𝑞, … ) dan 𝑄(𝑝, 𝑞, … ) disebut EKIVALEN secara
logika 𝑃(𝑝, 𝑞, … ) ⟺ 𝑄(𝑝, 𝑞, … ) jika keduanya mempunyai tabel kebenaran yang
identik.

18. Hukum identitas
(i) 𝑝 ∨ 𝐹 ⟺ 𝑝 (ii) 𝑝 ∧ 𝑇 ⟺ 𝑝
Hukum null / dominasi
(i) 𝑝 ∧ 𝐹 ⟺ 𝐹 (ii) 𝑝 ∨ 𝑇 ⟺ 𝑇
Hukum negasi
(i) 𝑝 ∨∼ 𝑝 ⟺ 𝑇 (ii)𝑝 ∧∼ 𝑝 ⟺ 𝐹
Hukum idempoten
(i) 𝑝 ∨ 𝑝 ⟺ 𝑝 (ii)𝑝 ∧ 𝑝 ⟺ 𝑝
Hukum involusi (negasi ganda)
(i) ∼ ∼ 𝑝 ⟺ 𝑝
Hukum penyerapan (absorpsi)
(i) 𝑝 ∨ 𝑝 ∧ 𝑞 ⟺ 𝑝 (ii) 𝑝 ∧ 𝑝 ∨ 𝑞 ⟺ 𝑝
Hukum komutatif
(i) 𝑝 ∨ 𝑞 ⟺ 𝑞 ∨ 𝑝 (ii) 𝑝 ∧ 𝑞 ⟺ 𝑞 ∧ 𝑝
Hukum asosiatif
(i) 𝑝 ∨ 𝑞 ∨ 𝑟 ⟺ 𝑝 ∨ 𝑞 ∨ 𝑟 (ii)𝑝 ∧ 𝑞 ∧ 𝑟 ⟺ 𝑝 ∧ 𝑞 ∧ 𝑟
Hukum distributif
(i) 𝑝 ∨ 𝑞 ∧ 𝑟 ⟺ 𝑝 ∨ 𝑞 ∧ 𝑝 ∨ 𝑟 (ii)𝑝 ∧ 𝑞 ∨ 𝑟 ⟺ 𝑝 ∧ 𝑞 ∨ 𝑝 ∧ 𝑟
Hukum De Morgan
(i) ∼ 𝑝 ∧ 𝑞 ⟺∼ 𝑝 ∨∼ 𝑞 (ii)∼ 𝑝 ∨ 𝑞 ⟺∼ 𝑝 ∧∼ 𝑞

19. Tunjukkan bahwa proposisi-proposisi di bawah ini keduanya ekivalen secara logika
menggunakan hukum logika
1. 𝑝 ∨∼ (𝑝 ∨ 𝑞) ⟺ 𝑝 ∨∼ 𝑞
2. 𝑝 ∧ 𝑝 ∨ 𝑞 ⟺ 𝑝
3. 𝑝 ∧ 𝑞 → 𝑝 ∨ 𝑞
4. 𝑝 ∧ 𝑝 → 𝑞 → 𝑞

20. 1. “Jika Air laut surut setelah gempa di laut, maka tsunami datang”
a. Air laut surut setelah gempa di laut. Karena itu tsunami datang.
b. Tsunami datang. Jadi, air laut surut setelah gempa di lault.
2. Jika 5 lebih kecil dari 4, maka 5 bukan bilangan prima.
5 tidak lebih kecil dari 4. Jadi, 5 adalah bilangan prima.
3. Jika 17 adalah bilangan prima, maka 3 tidak habis membagi 17.
3 habis membagi 17. Jadi, 17 bukan bilangan prima.

22. 1. Sebuah pulau didiami oleh dua suku asli. Penduduk suku pertama selalu
mengatakan hal yang benarm sedangkan penduduk dari suku lain selalu
mengatakan kebohongan. Anda tiba di pulau ini dan bertanya kepada seorang
penduduk setempat apakah di pulau tersebut ada emas atau tidak. Ia menjawab
“Ada emas di pulau ini jika dan hanya jika saya selalu mengatakan kebenaran”.
Apakah ada emas di pulau tersebut ?
2. Sebagian besar orang percaya bahwa harimau Jawa sudah lama punah. Tetapi,
pada suatu hari Amir membuta pernyataan-pernyataan kontroversial sebagai berikut :
a. Saya melihat harimau di hutan
b. Jika saya melihat harimau di hutan, maka saya juga melihat serigala.
Misalkan kita diberitahu bahwa Amir kadang-kadang suka berbohong dan kadang-
kadang jujur. Gunakan tabel kebenaran untuk memeriksa apakah Amir benar-benar
melihat harimau di hutan !

23. 3. Ada sebuah kampung yang penduduknya selalu mengatakan hal yang benar atau
selalu bohong. Penduduk kampung hanya memberikan jawaban “ya” atau “tidak”
terhadap pertanyaan yang diajukan oleh pendatang. Misalkan Anda adalah seorang
penatang yang baru sampai ke kampung tersebut dan hendak pergi ke kampung lain.
Anda sedang berada pada sebuah pertigaan jalan. Satu cabang jalan menuju kota,
sedangkan cabang jalan lainnya menuju jurang, namun Anda tidak tahu cabang mana
yang menuju ke kota tujuan (tidak ada penunjuk arah). Kebetulan di pertigaan
tersebut ada seorang warga kampung sedang berdiri, namanya Z. Sebutkan sebuat
pertanyaan yang harus Anda ajukan ke warga tersebut untuk menentukan cabang
jalan mana yang akan Anda ambil?
Petunjuk : Misalkan 𝑝 adalah pernyataan ,”Z selalu mengatakan sebenarnya” dan 𝑞
pernyataan “jalan yang berbelok ke kiri menuju kota”. Formulasikan pernyataan A yang
tersusun dari 𝑝 an 𝑞 sedemikian rupa sehingga Z akan menjawab pertanyaan “Apakah
A benar” dengan “ya” jika dan hanya jika 𝑞 benar.