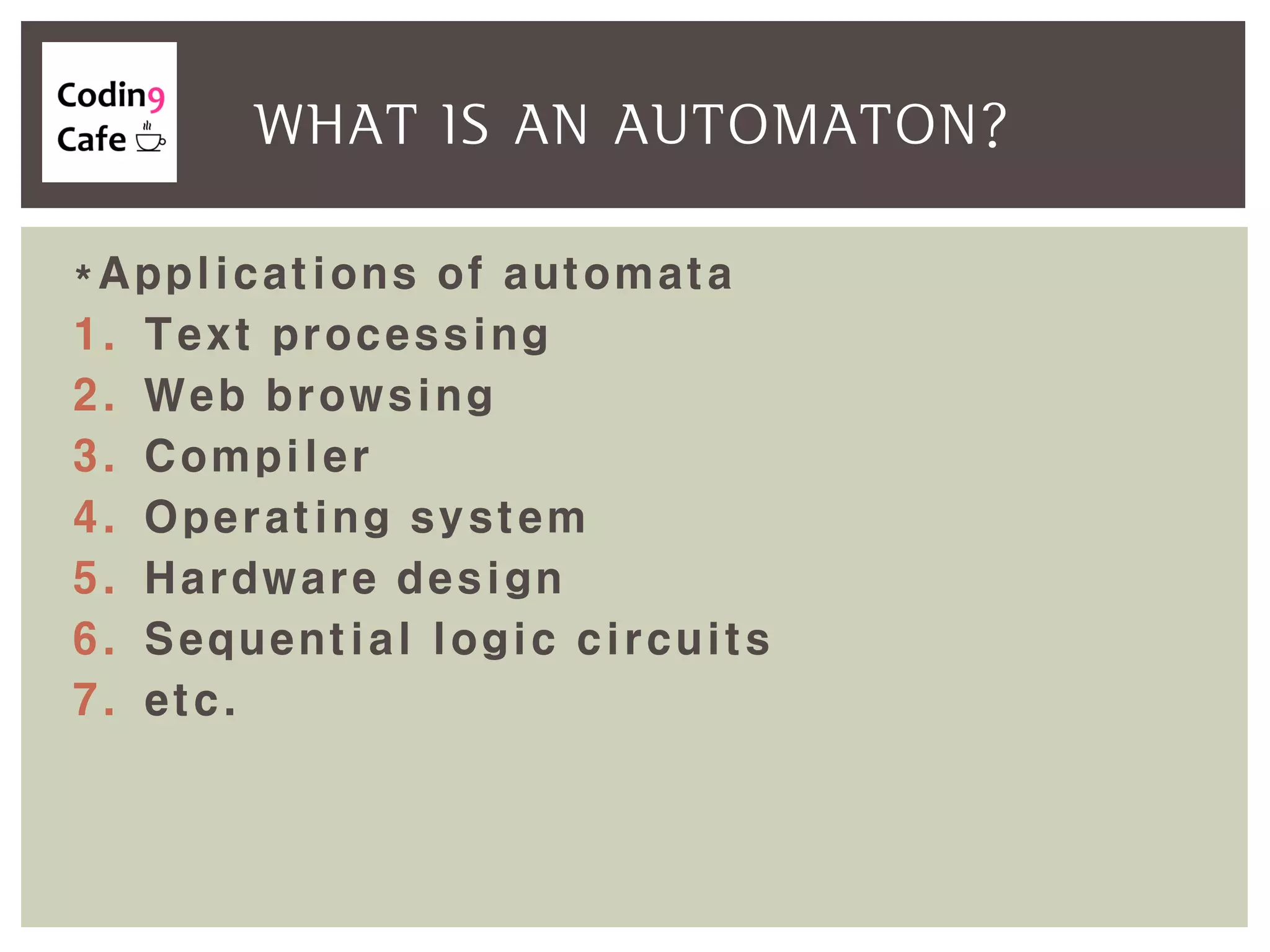
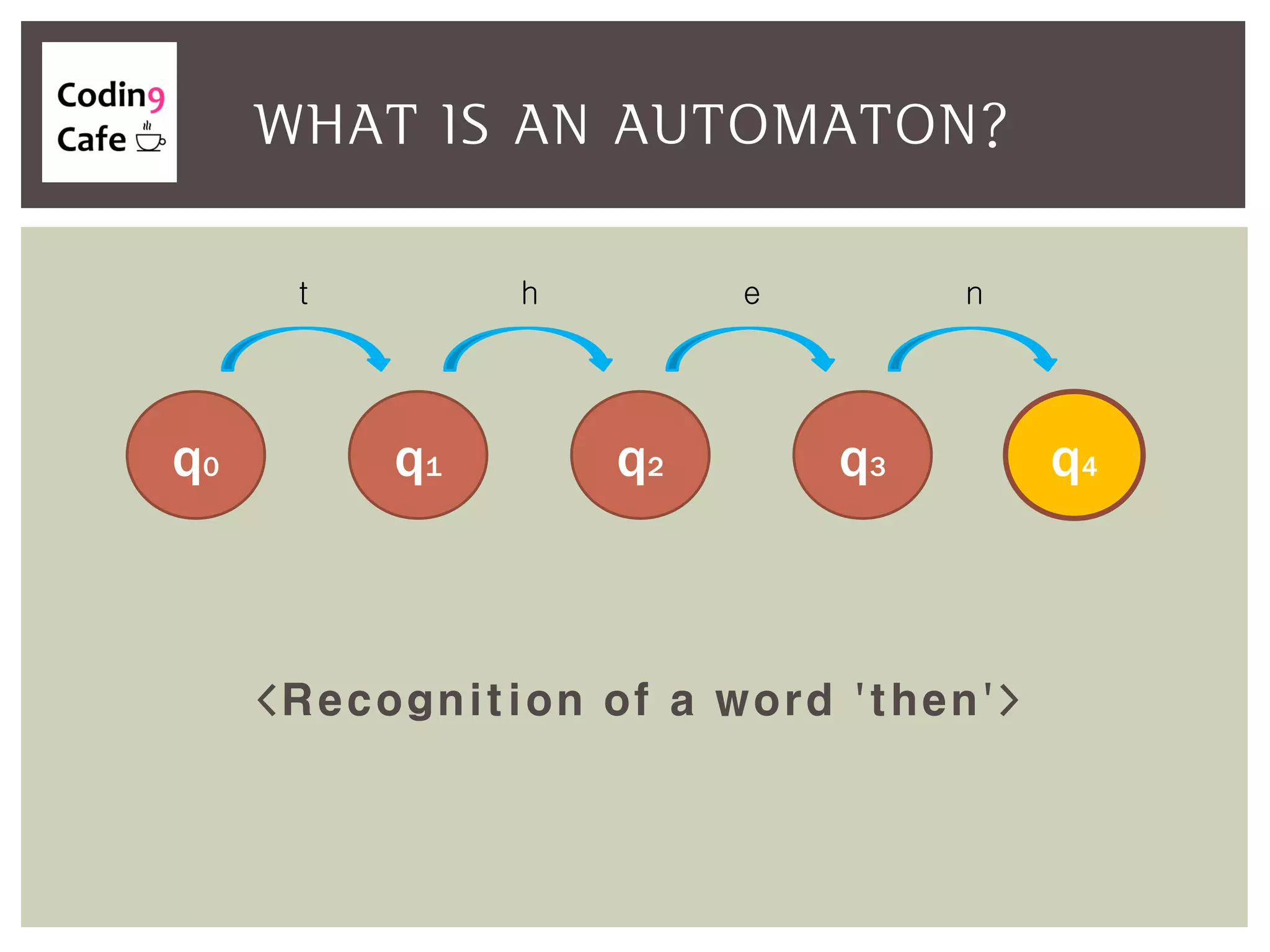
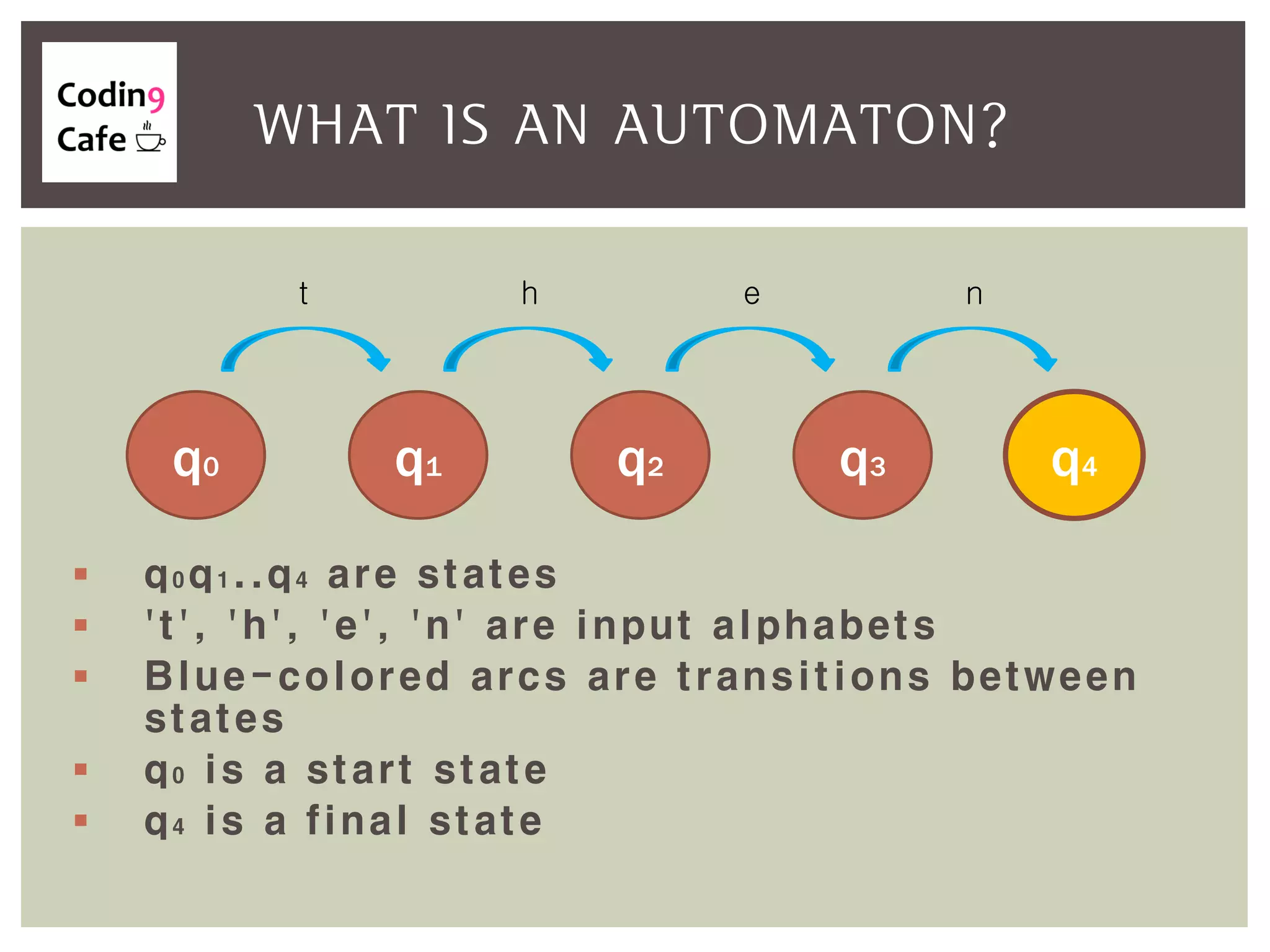
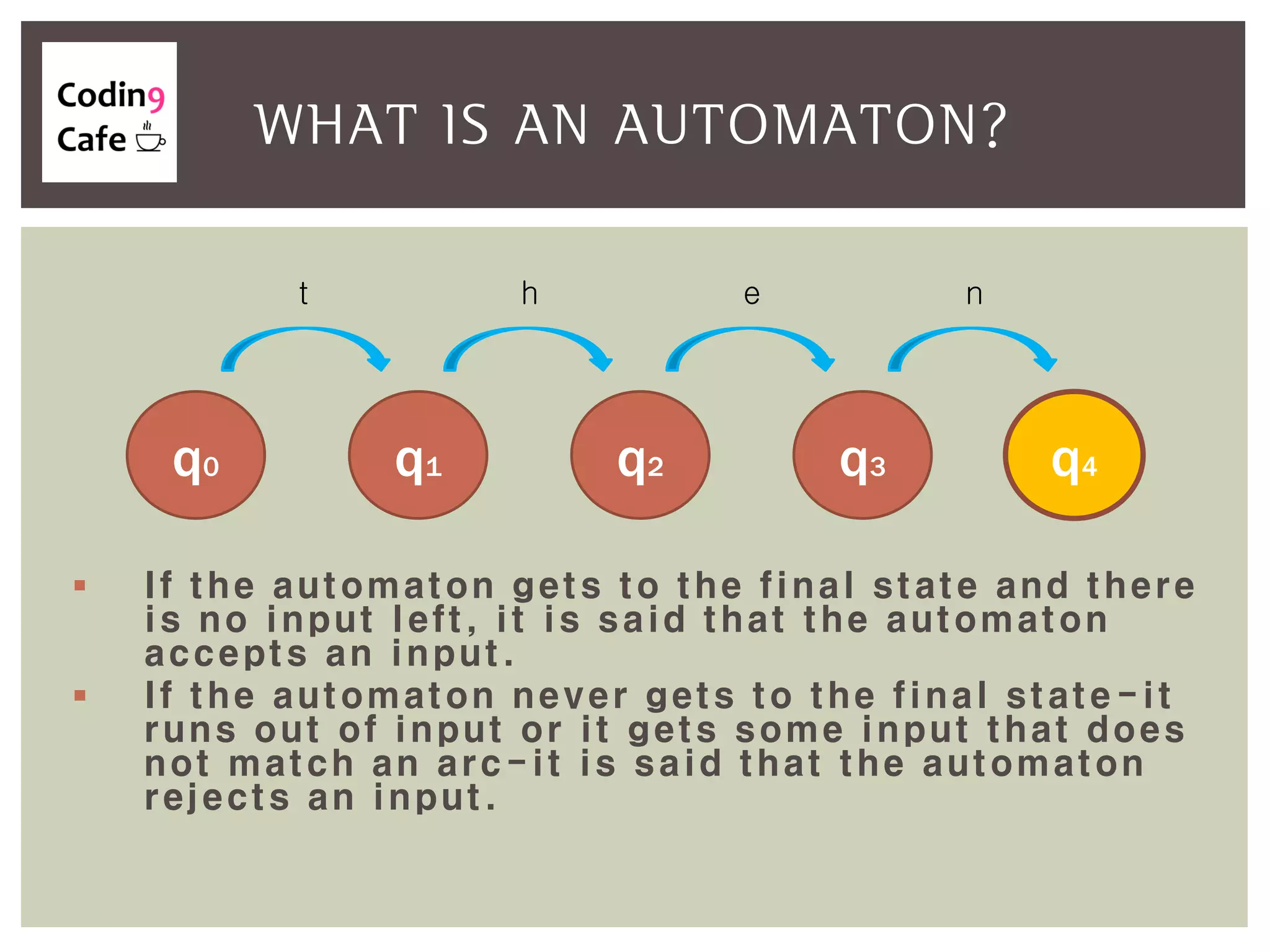
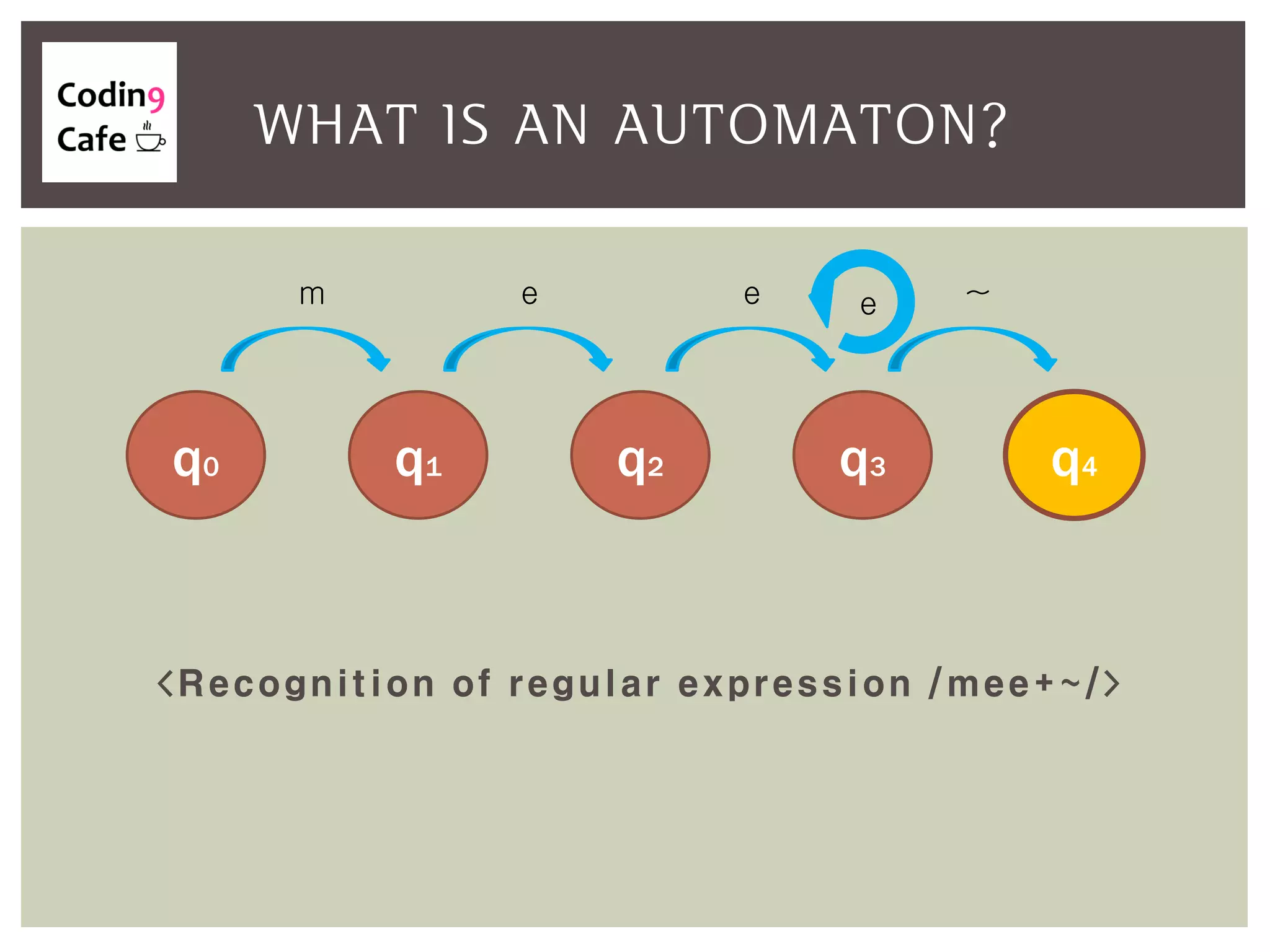
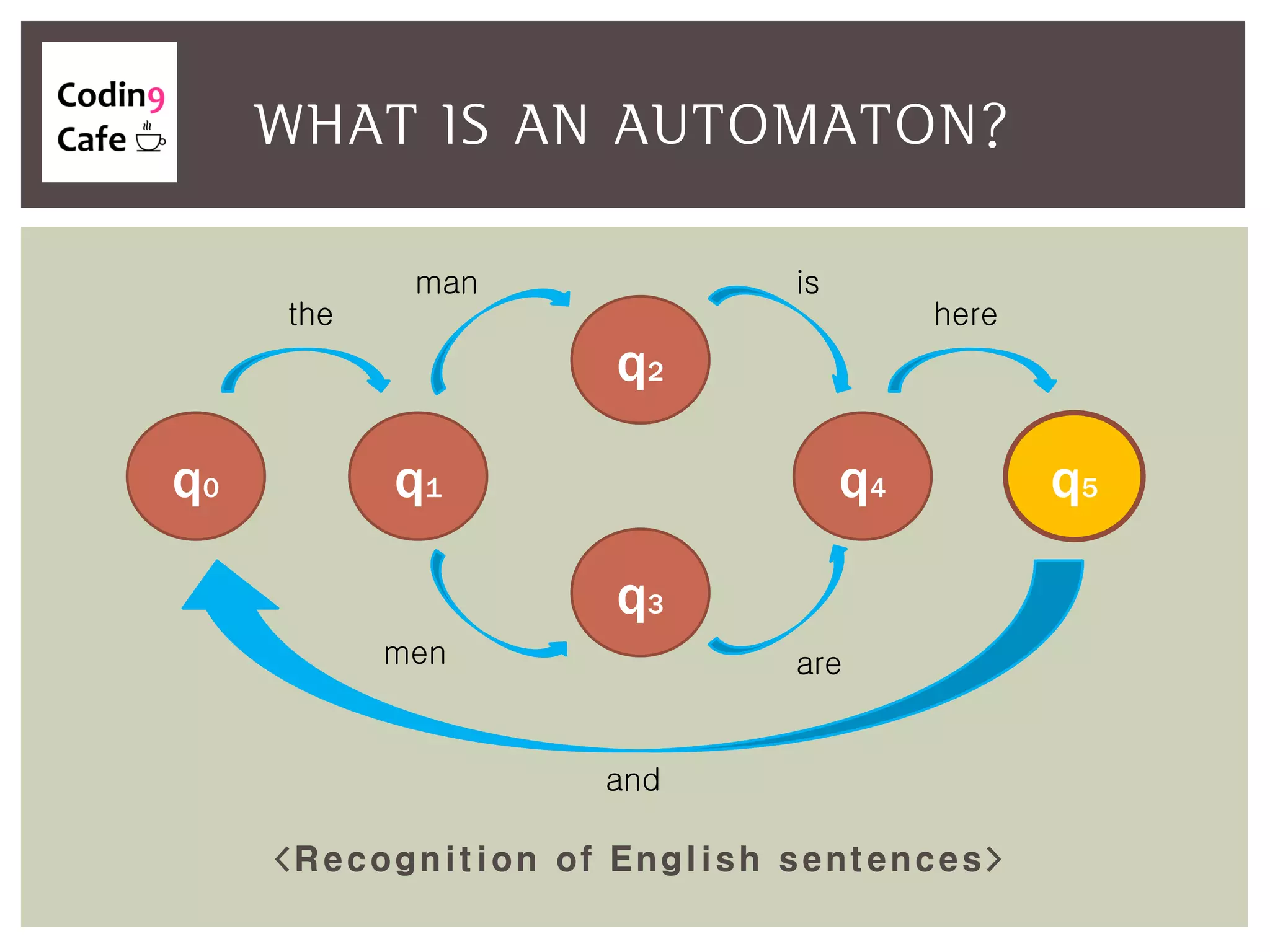
An automaton is an abstract computing machine central to the theory of computation, emerging from Turing's model in the 1950s. It processes inputs through states and transitions to determine acceptance of these inputs according to defined languages and grammars. Finite-state automata are characterized by a set of states, an input alphabet, a start state, final states, and a transition function.

1. 홍은기
AUTOMATA

2. 1. What is an Automaton?
2. Fundamental Concepts
3. Finite-state Automaton
4. References
CONTENTS

3. 1. The automaton (pl. automata) is an abstract
computing machine, which is a conceptual
model of the fundamentals of computation.
2. Automaton, originally from a Greek word
αὐτόματον, means "self-acting".
3. The automaton arose in the 1950s out of
Turing's (1936) model of algorithmic
computation, considered by many to be the
foundation of modern computer science.
WHAT IS AN AUTOMATON?

4. *Applications of automata
1. Text processing
2. Web browsing
3. Compiler
4. Operating system
5. Hardware design
6. Sequential logic circuits
7. etc.
WHAT IS AN AUTOMATON?

5. <Recognition of a word 'then'>
WHAT IS AN AUTOMATON?
q0 q1 q2 q3
t h e
q4
n

6.  q0q1..q4 are states
 't', 'h', 'e', 'n' are input alphabets
 Blue-colored arcs are transitions between
states
 q0 is a start state
 q4 is a final state
WHAT IS AN AUTOMATON?
q0 q1 q2 q3
t h e
q4
n

7.  If the automaton gets to the final state and there
is no input left, it is said that the automaton
accepts an input.
 If the automaton never gets to the final state-it
runs out of input or it gets some input that does
not match an arc-it is said that the automaton
rejects an input.
WHAT IS AN AUTOMATON?
q0 q1 q2 q3
t h e
q4
n

8. <Recognition of regular expression /mee+~/>
WHAT IS AN AUTOMATON?
q0 q1 q2 q3
m e e
q4
~e

9. <Recognition of English sentences>
WHAT IS AN AUTOMATON?
and
q0 q1
q2
q4
the
man is
q5
here
q3
men are

10. 1. An alphabet is a set of symbols.
2. A string is a set of alphabets.
3. The set of all the strings accepted by an
automaton is called the language
recognized by the automaton.
4. A grammar is a formal counterpart of an
automaton which is more focused on the
aspect of the generation of a language.
5. The usefulness of an automaton for
defining a language is that it can express
an infinite set in a closed form.
FUNDAMENTAL CONCEPTS

11. 1. An alphabet is a set of symbols.
2. A string is a set of alphabets.
3. The set of all the strings accepted by an
automaton is called the language
recognized by the automaton.
4. A grammar is a formal counterpart of an
automaton which is more focused on the
aspect of the generation of a language.
5. The usefulness of an automaton for
defining a language is that it can express
an infinite set in a closed form.
FUNDAMENTAL CONCEPTS
L(m) = {mee~, meee~, meeee~, meeeee~….}
The language characterized by a model m
(The regular expression /mee+~/, in this case.)

12. A finite-state automaton is defined by five
parameters
 A = (Q, ∑, q₀, F, δ)
 Q = q₀ q₁q₂...qN-1: a finite set of N states.
 ∑ = a finite input alphabet of symbols.
 q₀ = the start state, q₀ ∈ Q
 F = the set of final states, F ⊆ Q
 δ(q,i): the transition function between states. Given a
state q ∈ Q and an input symbol i ∈ ∑, δ(q,i) returns
a new state q′ ∈ Q. δ is thus a relation from Q × ∑
to Q.
FINITE-STATE AUTOMATON

13. 김삼묘, 유기영. (2004). 계산모델: 오토마타 및 형식
언어. 이한출판사
Jurafsky, D. and Martin, J. H. (2009).
Speech and language processing 2nd
Edition. Pearson Education, Inc.
Partee et al. (1993). Mathematical methods
in linguistics. Kluwer Academic
Publishers
REFERENCES