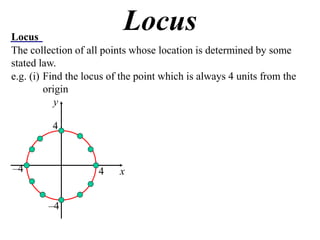
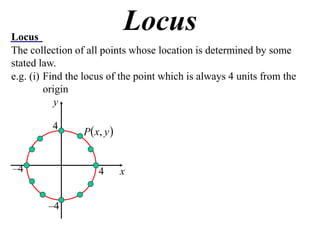
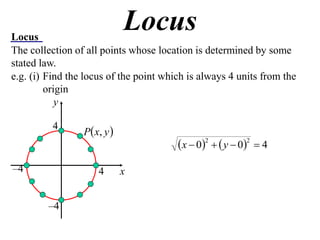
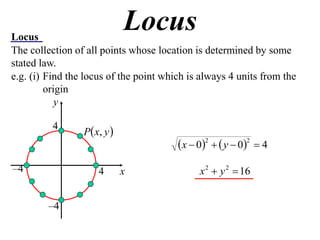
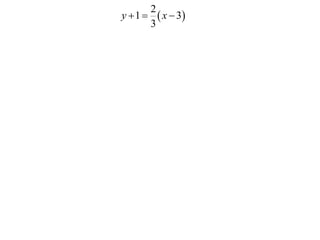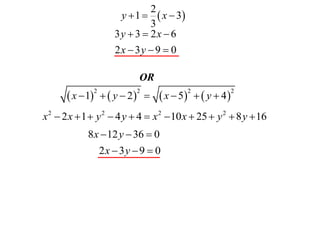The document defines locus as the collection of all points whose location is determined by some stated law. It provides examples of finding the locus of points that are: 1) Always 4 units from the origin, which is a circle with radius 4 centered at the origin. 2) Always 5 units from the y-axis, which is the line y=±5. 3) Always 3 units from the line y=x+1, which is the pair of parallel lines that are a distance of 3 units above and below that line.

1. Locus

2. Locus
Locus
The collection of all points whose location is determined by some
stated law.

3. Locus
Locus
The collection of all points whose location is determined by some
stated law.
e.g. (i) Find the locus of the point which is always 4 units from the
origin

4. Locus
Locus
The collection of all points whose location is determined by some
stated law.
e.g. (i) Find the locus of the point which is always 4 units from the
origin
y
x

5. Locus
Locus
The collection of all points whose location is determined by some
stated law.
e.g. (i) Find the locus of the point which is always 4 units from the
origin
y
4 x

6. Locus
Locus
The collection of all points whose location is determined by some
stated law.
e.g. (i) Find the locus of the point which is always 4 units from the
origin
y
4
4 x

7. Locus
Locus
The collection of all points whose location is determined by some
stated law.
e.g. (i) Find the locus of the point which is always 4 units from the
origin
y
4
–4 4 x

8. Locus
Locus
The collection of all points whose location is determined by some
stated law.
e.g. (i) Find the locus of the point which is always 4 units from the
origin
y
4
–4 4 x
–4

9. Locus
Locus
The collection of all points whose location is determined by some
stated law.
e.g. (i) Find the locus of the point which is always 4 units from the
origin
y
4
–4 4 x
–4

10. Locus
Locus
The collection of all points whose location is determined by some
stated law.
e.g. (i) Find the locus of the point which is always 4 units from the
origin
y
4
–4 4 x
–4

11. Locus
Locus
The collection of all points whose location is determined by some
stated law.
e.g. (i) Find the locus of the point which is always 4 units from the
origin
y
P  x, y 
4
–4 4 x
–4

12. Locus
Locus
The collection of all points whose location is determined by some
stated law.
e.g. (i) Find the locus of the point which is always 4 units from the
origin
y
P  x, y 
4
 x  02   y  02  4
–4 4 x
–4

13. Locus
Locus
The collection of all points whose location is determined by some
stated law.
e.g. (i) Find the locus of the point which is always 4 units from the
origin
y
P  x, y 
4
 x  02   y  02  4
–4 4 x x 2  y 2  16
–4

14. (ii) A point moves so that it is always 5 units away from the y axis

15. (ii) A point moves so that it is always 5 units away from the y axis
y
x

16. (ii) A point moves so that it is always 5 units away from the y axis
y
P  x, y 
x

17. (ii) A point moves so that it is always 5 units away from the y axis
y
 0, y  5 P x, y 
x

18. (ii) A point moves so that it is always 5 units away from the y axis
y
 0, y  5 P x, y 
 x  0   y  y   5
2 2
x

19. (ii) A point moves so that it is always 5 units away from the y axis
y
 0, y  5 P x, y 
 x  0   y  y   5
2 2
x x 2  25

20. (ii) A point moves so that it is always 5 units away from the y axis
y
 0, y  5 P x, y 
 x  0   y  y   5
2 2
x x 2  25
x  5

21. (ii) A point moves so that it is always 5 units away from the y axis
y
 0, y  5 P x, y 
 x  0   y  y   5
2 2
x x 2  25
x  5
(iii) A point moves so that it is always 3 units away from the line y = x + 1

22. (ii) A point moves so that it is always 5 units away from the y axis
y
 0, y  5 P x, y 
 x  0   y  y   5
2 2
x x 2  25
x  5
(iii) A point moves so that it is always 3 units away from the line y = x + 1
y
x

23. (ii) A point moves so that it is always 5 units away from the y axis
y
 0, y  5 P x, y 
 x  0   y  y   5
2 2
x x 2  25
x  5
(iii) A point moves so that it is always 3 units away from the line y = x + 1
y y  x 1
1
–1 x

24. (ii) A point moves so that it is always 5 units away from the y axis
y
 0, y  5 P x, y 
 x  0   y  y   5
2 2
x x 2  25
x  5
(iii) A point moves so that it is always 3 units away from the line y = x + 1
y y  x 1
P  x, y 
1
–1 x

25. (ii) A point moves so that it is always 5 units away from the y axis
y
 0, y  5 P x, y 
 x  0   y  y   5
2 2
x x 2  25
x  5
(iii) A point moves so that it is always 3 units away from the line y = x + 1
y y  x 1
P  x, y 
1
–1 x

26. (ii) A point moves so that it is always 5 units away from the y axis
y
 0, y  5 P x, y 
 x  0   y  y   5
2 2
x x 2  25
x  5
(iii) A point moves so that it is always 3 units away from the line y = x + 1
y y  x 1 x  y 1
P  x, y  3
12   1
2
1
–1 x

27. (ii) A point moves so that it is always 5 units away from the y axis
y
 0, y  5 P x, y 
 x  0   y  y   5
2 2
x x 2  25
x  5
(iii) A point moves so that it is always 3 units away from the line y = x + 1
y y  x 1 x  y 1
P  x, y  3
12   1
2
1
x  y 1  3 2
–1 x

28. (ii) A point moves so that it is always 5 units away from the y axis
y
 0, y  5 P x, y 
 x  0   y  y   5
2 2
x x 2  25
x  5
(iii) A point moves so that it is always 3 units away from the line y = x + 1
y y  x 1 x  y 1
P  x, y  3
12   1
2
1
x  y 1  3 2
–1 x
x  y 1  3 2

29. (ii) A point moves so that it is always 5 units away from the y axis
y
 0, y  5 P x, y 
 x  0   y  y   5
2 2
x x 2  25
x  5
(iii) A point moves so that it is always 3 units away from the line y = x + 1
y y  x 1 x  y 1
P  x, y  3
12   1
2
1
x  y 1  3 2
–1 x
x  y 1  3 2 or   x  y  1  3 2

30. (ii) A point moves so that it is always 5 units away from the y axis
y
 0, y  5 P x, y 
 x  0   y  y   5
2 2
x x 2  25
x  5
(iii) A point moves so that it is always 3 units away from the line y = x + 1
y y  x 1 x  y 1
P  x, y  3
12   1
2
1
x  y 1  3 2
–1 x
x  y 1  3 2 or   x  y  1  3 2
x  y 1 3 2  0

31. (ii) A point moves so that it is always 5 units away from the y axis
y
 0, y  5 P x, y 
 x  0   y  y   5
2 2
x x 2  25
x  5
(iii) A point moves so that it is always 3 units away from the line y = x + 1
y y  x 1 x  y 1
P  x, y  3
12   1
2
1
x  y 1  3 2
–1 x
x  y 1  3 2 or   x  y  1  3 2
x  y 1 3 2  0 x  y 1  3 2

32. (ii) A point moves so that it is always 5 units away from the y axis
y
 0, y  5 P x, y 
 x  0   y  y   5
2 2
x x 2  25
x  5
(iii) A point moves so that it is always 3 units away from the line y = x + 1
y y  x 1 x  y 1
P  x, y  3
12   1
2
1
x  y 1  3 2
–1 x
x  y 1  3 2 or   x  y  1  3 2
x  y 1 3 2  0 x  y 1  3 2
x  y 1 3 2  0

33. (iv) A point moves so that its distance from the x axis is always 5 times
as great as its distance from the y axis.

34. (iv) A point moves so that its distance from the x axis is always 5 times
as great as its distance from the y axis.
y
x

35. (iv) A point moves so that its distance from the x axis is always 5 times
as great as its distance from the y axis.
P  x, y 
y
x

36. (iv) A point moves so that its distance from the x axis is always 5 times
as great as its distance from the y axis.
P  x, y 
y
 x,0  x

37. (iv) A point moves so that its distance from the x axis is always 5 times
as great as its distance from the y axis.
P  x, y 
y
 0, y 
 x,0  x

38. (iv) A point moves so that its distance from the x axis is always 5 times
as great as its distance from the y axis.
P  x, y 
y d
 0, y 
5d
 x,0  x

39. (iv) A point moves so that its distance from the x axis is always 5 times
as great as its distance from the y axis.
P  x, y 
y d
 0, y 
 x  x    y  0  5  x  0   y  y 
2 2 2 2
5d
 x,0  x

40. (iv) A point moves so that its distance from the x axis is always 5 times
as great as its distance from the y axis.
P  x, y 
y d
 0, y 
 x  x    y  0  5  x  0   y  y 
2 2 2 2
5d
y 2  25 x 2
 x,0  x

41. (iv) A point moves so that its distance from the x axis is always 5 times
as great as its distance from the y axis.
P  x, y 
y d
 0, y 
 x  x    y  0  5  x  0   y  y 
2 2 2 2
5d
y 2  25 x 2
 x,0  x y  5 x

42. (iv) A point moves so that its distance from the x axis is always 5 times
as great as its distance from the y axis.
P  x, y 
y d
 0, y 
 x  x    y  0  5  x  0   y  y 
2 2 2 2
5d
y 2  25 x 2
 x,0  x y  5 x
(v) A point moves so that its distance from (1,2) is the same as its
distance from (5,–4).

43. (iv) A point moves so that its distance from the x axis is always 5 times
as great as its distance from the y axis.
P  x, y 
y d
 0, y 
 x  x    y  0  5  x  0   y  y 
2 2 2 2
5d
y 2  25 x 2
 x,0  x y  5 x
(v) A point moves so that its distance from (1,2) is the same as its
distance from (5,–4).
y
x

44. (iv) A point moves so that its distance from the x axis is always 5 times
as great as its distance from the y axis.
P  x, y 
y d
 0, y 
 x  x    y  0  5  x  0   y  y 
2 2 2 2
5d
y 2  25 x 2
 x,0  x y  5 x
(v) A point moves so that its distance from (1,2) is the same as its
distance from (5,–4).
y
1, 2 
x
 5, 4 

45. (iv) A point moves so that its distance from the x axis is always 5 times
as great as its distance from the y axis.
P  x, y 
y d
 0, y 
 x  x    y  0  5  x  0   y  y 
2 2 2 2
5d
y 2  25 x 2
 x,0  x y  5 x
(v) A point moves so that its distance from (1,2) is the same as its
distance from (5,–4).
y
1, 2 
P  x, y  x
 5, 4 

46. (iv) A point moves so that its distance from the x axis is always 5 times
as great as its distance from the y axis.
P  x, y 
y d
 0, y 
 x  x    y  0  5  x  0   y  y 
2 2 2 2
5d
y 2  25 x 2
 x,0  x y  5 x
(v) A point moves so that its distance from (1,2) is the same as its
distance from (5,–4).
y
1, 2 
P  x, y  x
 5, 4 

47. (iv) A point moves so that its distance from the x axis is always 5 times
as great as its distance from the y axis.
P  x, y 
y d
 0, y 
 x  x    y  0  5  x  0   y  y 
2 2 2 2
5d
y 2  25 x 2
 x,0  x y  5 x
(v) A point moves so that its distance from (1,2) is the same as its
distance from (5,–4).
y Perpendicular bisector of (1,2) and (5,–4)
1, 2 
P  x, y  x
 5, 4 

48. (iv) A point moves so that its distance from the x axis is always 5 times
as great as its distance from the y axis.
P  x, y 
y d
 0, y 
 x  x    y  0  5  x  0   y  y 
2 2 2 2
5d
y 2  25 x 2
 x,0  x y  5 x
(v) A point moves so that its distance from (1,2) is the same as its
distance from (5,–4).
y Perpendicular bisector of (1,2) and (5,–4)
4  2
1, 2  mAB 
5 1
P  x, y  6
x 
4
 5, 4  3

2

49. (iv) A point moves so that its distance from the x axis is always 5 times
as great as its distance from the y axis.
P  x, y 
y d
 0, y 
 x  x    y  0  5  x  0   y  y 
2 2 2 2
5d
y 2  25 x 2
 x,0  x y  5 x
(v) A point moves so that its distance from (1,2) is the same as its
distance from (5,–4).
y Perpendicular bisector of (1,2) and (5,–4)
4  2
1, 2  mAB 
5 1
P  x, y  6
x 
4
 5, 4  3

2 2
 required slope 
3

50. (iv) A point moves so that its distance from the x axis is always 5 times
as great as its distance from the y axis.
P  x, y 
y d
 0, y 
 x  x    y  0  5  x  0   y  y 
2 2 2 2
5d
y 2  25 x 2
 x,0  x y  5 x
(v) A point moves so that its distance from (1,2) is the same as its
distance from (5,–4).
y Perpendicular bisector of (1,2) and (5,–4)
4  2
1, 2  mAB   1  5 4  2 
M AB  
5 1 , 
 2 2 
P  x, y  6
x    3, 1
4
 5, 4  3

2 2
 required slope 
3

51. 2
y  1   x  3
3

52. 2
y  1   x  3
3
3y  3  2x  6
2x  3y  9  0

53. 2
y  1   x  3
3
3y  3  2x  6
2x  3y  9  0
OR

54. 2
y  1   x  3
3
3y  3  2x  6
2x  3y  9  0
OR
 x  1   y  2    x  5   y  4 
2 2 2 2

55. 2
y  1   x  3
3
3y  3  2x  6
2x  3y  9  0
OR
 x  1   y  2    x  5   y  4 
2 2 2 2
x 2  2 x  1  y 2  4 y  4  x 2  10 x  25  y 2  8 y  16

56. 2
y  1   x  3
3
3y  3  2x  6
2x  3y  9  0
OR
 x  1   y  2    x  5   y  4 
2 2 2 2
x 2  2 x  1  y 2  4 y  4  x 2  10 x  25  y 2  8 y  16
8 x  12 y  36  0

57. 2
y  1   x  3
3
3y  3  2x  6
2x  3y  9  0
OR
 x  1   y  2    x  5   y  4 
2 2 2 2
x 2  2 x  1  y 2  4 y  4  x 2  10 x  25  y 2  8 y  16
8 x  12 y  36  0
2x  3 y  9  0

58. 2
y  1   x  3
3
3y  3  2x  6
2x  3y  9  0
OR
 x  1   y  2    x  5   y  4 
2 2 2 2
x 2  2 x  1  y 2  4 y  4  x 2  10 x  25  y 2  8 y  16
8 x  12 y  36  0
2x  3 y  9  0
Exercise 9A; 1aceg, 3a, 4, 6, 8, 10, 11, 13, 14