Chapter 4(differentiation)

BMM 104: ENGINEERING MATHEMATICS I Page 1 of 16

CHAPTER 4: DIFFERENTIATION

The Derivative as a Function

Derivative Function

The derivative of the function f(x) with respect to the variable x is the function f ' whose value
at x is

f( x + h)− f( x)
f ' ( x ) = lim ,
h →0 h
provided the limit exists.

Example: Attend lecture.

PROBLEM SET: CHAPTER 4

Find the following indicated derivatives by using definition.

1
1. y = 2x3 4. v =t −
t
s3 1
2. r= +1 5. p=
2 q +1
t 1
3. s= 6. z=
2t + 1 3w − 2

ANSWERS FOR PROBLEM SET: CHAPTER 4


Find the following indicated derivatives by using definition.

1
1. 6 x2 4. 1+
t2
3 2 −1
2. s 5.
2 2( q + 1 ) 3 / 2
1 −3
3. 6.
( 2t + 1 ) 2 2( 3w − 2 ) 3 / 2

Differentiation Rules

Derivative of a Constant Function

df d
If f has the constant value f(x) = c, then dx
=
dx
( c ) =0

Power Rule for Positive Integers

If n is a positive integer, then

d n
x = nx n −1
dx

Constant Multiple Rule


d du
If u is a differentiable function of x, and c is a constant, then dx
( cu ) = c
dx

Derivative Sum Rule

If u and v are differentiable functions of x, then their sum u + v is differentiable at every point
d du dv
where u and v are both differentiable. At such points, dx
( u +v ) =
dx
+
dx

Derivative Product Rule


If u and v are differentiable at x, then so is their product uv, and

d dv du
( uv ) = u +v
dx dx dx

Derivative Quotient Rule

If u and v are differentiable at x and if v( x ) ≠ 0 , then the quotient u/v is differentiable at x, and

du dv
v −u
d u  dx dx
 =
dx  v  v2



Derivative Calculations

Find the first and second derivatives for the following functions.

1
1. y = −x 2 + 3 7. w = 3 z −2 −
z
4
2. y = x2 + x + 8 8. s = −2t −1 +
t2
3. s = 5t 3 − 3t 5 9. y = 6 x 2 − 10 x − 5 x −2
4. w = 3 z 7 − 7 z 3 + 21z 2 10. y = 4 − 2 x − x −3
4x3 1 5
5. y= −x 11. r= 2
−
3 3s 2s
x3 x2 x 12 4 1
6. y= + + 12. r= − 3+ 4
3 2 4 θ θ θ

In the following questions, find y ' (a) by applying the Product Rule and (b) by multiplying the
factors to produce a sum of simpler terms to differentiate.

1
1. y = ( 3 − x 2 )( x 3 − x + 1 ) 3. y = ( x 2 + 1 )( x + 5 + )
x
 1  1 
2. y = ( x − 1 )( x 2 + x + 1 ) 4. y =  x +  x − + 1
 x  x 

Differentiate the following functions.

2x + 5 s −1
1. y= 7. f(s)=
3x − 2 s +1


2x + 1 5x + 1
2. z= 8. u=
x2 − 1 2 x
x2 − 4 1 + x −4 x
3. g( x ) = 9. v=
x + 0.5 x
t2 −1  1 
4. f (t ) = 10. r = 2
 + θ

t2 + t − 2  θ 
1
v = ( 1 − t )( 1 + t 2 ) −1 y=
5. 11.
( x − 1)( x 2 + x + 1)
2

y=
( x + 1)( x + 2 )
6. w = ( 2 x − 7 ) −1 ( x + 5 ) 12.
( x − 1)( x − 2 )


Derivative Calculations

1. -2 7. 18 z −4 − 2 z −3
2. 2 8. − 4t −3 + 24t −4
3. 30t − 60t 3 9. 12 − 30 x −4
4. 126 z 5 − 42 z + 42 10. −12 x −5
5. 8x 11. 2 s −4 − 5 s −3
6. 2x + 1 12. 24θ −3 − 48θ −5 + 20θ −6

1. − 5 x 4 + 12 x 2 − 2 x − 3 3. 3 x 2 + 10 x + 2 − x −2
2. 3x 2 4. 2 x + 1 − x −2 + 2 x −3

− 19 1
1. 7.
( 3 x − 2 )2 s ( s + 1 )2
− 2( x 2 + x + 1 ) 5x −1
2. 8.
( x 2 − 1 )2 4x3 / 2
x2 + x + 4 2 x −1
3. 9.
( x + 0.5 ) 2 x2
1 1 1
4. 10. − +
( t + 2 )2 θ 3/ 2
θ 1/ 2

t − 2t − 1
2
− 4 x − 3x 2 + 1
3

5. 11.
( 1 + t 2 )2 ( x 2 − 1 )2 ( x 2 + x + 1 )2
− 17 − 6( x 2 − 2 )
6. 12.
( 2 x − 7 )2 ( x − 1 )2 ( x − 2 )2


Derivatives of Trigonometric Functions

d
1. sin x = cos x
dx
d
2. cos x = − sin x
dx
d
3. tan x = sec 2 x
dx
d
4. sec x = sec x tan x
dx
d
5. cot x = − csc 2 x
dx
d
6. csc x = − csc x cot x
dx


PROBLEM SET 3.3


dy
Find .
dx

cot x
1. y = −10 x + 3 cos x 7. y=
1 + cot x
3 cos x
2. y= + 5 sin x 8. y=
x 1 + sin x
4 1
3. y = csc x −4 x +7 9. y= +
cos x tan x
1 cos x x
4. y = x 2 cot x − 10. y= +
x2 x cos x
5. y = ( sec x + tan x )( sec x − tan x ) 11. y = x 2 sin x + 2 x cos x − 2 sin x
6. y = ( sin x + cos x ) sec x 12. y = x 2 cos x − 2 x sin x − 2 cos x


− csc 2 x
1. − 10 − 3 sin x 7.
( 1 + cot x ) 2
−1
2. − 3 x −2 + 5 cos x 8.
1 + sin x


2
3. − csc x cot x − 9. 4 sec x tan x − csc 2 x
x
− x sin x − cos x cos x + x sin x
4. − x 2 csc 2 x + 2 x cot x + 2 x −3 10. +
x2 cos 2 x
5. 0 11. x 2 cos x
6. sec 2 x 12. − x 2 sin x

The Chain Rule

If f(u) is differentiable at the point u = g(x) and g(x) is differentiable at x, then the composite
function ( f  g )( x ) = f ( g ( x )) is differentiable at x, and

( f  g )' ( x ) = f ' ( g ( x )) • g ' ( x )

In Leibniz’s notation, if y = f(u) and u = g(x), then

dy dy du
= • ,
dx du dx
where dy/du is evaluated at u = g(x).



Differentiate the following functions.

y = ( 2 x +1) y = ( 4 x + 3 ) 4 ( x + 1 ) −3
5
1. 21.
y = (4 − 3 x) y = ( 2 x − 5 ) −1 ( x 2 − 5 x )6
9
2. 22.
−7
 x
3. y = 1 −  23. h( x ) = x tan( 2 x ) +7
 7
−10
x  1
4. y =  − 1 24. k ( x ) = x 2 sec 
2  x
4 2
 x2 1  sin θ 
5. y =
 8 +x− x
 25. f (θ ) =  
   1 + cos θ 
5 −1
x 1   1 + cos t 
6. y = +  26. g( t ) =  
 5 5x   sin t 
7. y = sec ( tan x ) 27. ( )
r = sin θ 2 cos( 2θ )
 1 1
8. y = cot π −  28. r = sec θ tan 
 x θ 


 t 
9. y = sin 3 x 29. q = sin
 

 t +1 
 sin t 
10. y = 5 cos −4 x 30. q = cot  
 t 
11. p= 3 −t 31. y = sin 2 ( πt − 2 )
12. q = 2r − r 2
32. y = sec 2 πt
4 4
13. s= sin 3t + cos 5t 33. y = ( 1 + cos 2t ) −4
3π 5π
 3πt   3πt 
14. s = sin  + cos  34. y = ( 1 + cot( t / 2 )) −2
 2   2 
r = ( csc θ + cot θ ) y = sin(cos( 2t − 5 ))
−1
15. 35.
  t 
r = −( sec θ + tan θ ) y = cos 5 sin   
−1
16. 36.  
  3 
3
  t 
17. y = x 2 sin 4 x + x cos −2 x 37. y =  1 + tan 4   
 
  12  

18. y=
1
x
x
sin −5 x − cos 3 x
3
38.
1
(
y = 1 + cos 2 ( 7 t )
6
) 3

−1
1  1 
19. y = ( 3 x − 2 )7 +  4 − 2  39. y = 1 + cos( t 2 )
21  2x 
4
12 
20. y = ( 5 − 2 x ) −3 +  + 1 40. y = 4 sin( 1+ t )
8x 


( 4 x + 3) 3 ( 4 x + 7 )
1. 10( 2 x + 1 ) 4
21.
( x + 1) 4
2( x 2 − 5 x )6
2. − 27( 4 − 3 x ) 8 22. 6( x 2 − 5 x )5 −
( 2 x − 5 )2
−8
 x
3. 1 −  23. x sec 2 ( 2 x ) + tan( 2 x )
 7
−11
x  1 1 1
4. − 5 − 1  24. 2 x sec  − sec  tan 
 2  x x x
2 sin θ
3
 x2 1 x 1 
5. 4
 8 + x − x   4 + 1 + x2 
 25.
    ( 1 + cos θ ) 2
4
x 1   1  1
6.  +  1 − 2  26.
 5 5x   x  1 + cos t


7. ( sec( tan x ) tan( tan x ) ) sec 2 x 27. − 2 sin (θ 2 ) sin ( 2θ ) + 2θ cos( 2θ ) cos(θ 2 )
 1  2  1 
−1  1 tan θ tanθ  sec θ 
8. csc 2 π −  28. ( sec θ )  −
θ2
 
x 2
 x  2 θ 
 
 
 t +2   t 
9. 3( sin 2 x ) cos x 29. 
 2( t + 1 )3 / 2  cos
  

   t +1
  sin t   t cos t − sin t 
10. 20(cos −5 x )(sin x ) 30.  − csc 2 
  
 
  t   t2 
−1
11. 31. 2π sin( πt − 2 ) cos( πt − 2 )
2 3 −t
1−r
12. 32. 2π sec 2 πt tan πt
2r − r 2
4 8 sin 2t
13. (cos 3t − sin 5t ) 33.
π ( 1 + cos 2t ) 5
t
csc 2  
3π 3πt 3πt 2
14. (cos − sin ) 34.
2 2 2 t
( 1 + cot   ) 3
2

csc θ
15. 35. − 2 cos(cos( 2t − 5 ))(sin( 2t − 5 ))
csc θ + cot θ

sec θ 5   t    t  
16. 36. − sin 5 sin   cos  
  
sec θ + tan θ 3   3    3  
17. 4 x 2 sin 3 x cos x + 2 x sin 4 x + 2 x sin x cos −3 x + cos −2 x
− 5 −6 1 1
18. sin x cos x − 2 sin −5 x + x cos 2 x sin x − cos 3 x
x x 3
1
( 3 x − 2 )6 − 
2
2 4  t   3 t  2  t 
19. 3
x 4 − 2 
1  37. 1 + tan  12  tan  12  sec  12 
       
 2x 
38. [ ] 2
− 7 1 + cos 2 ( 7 t ) (cos( 7 t ) sin( 7 t ))
t sin (t 2 )
39. −
1 + cos( t 2 )
3
2 
 + 1 cos 1 + t 
 
20. 6 40.  
− 2 
x
t+ t
( 5 − 2 x )4 x

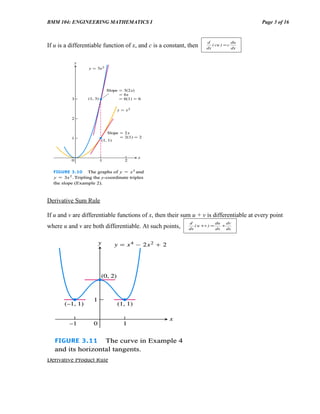
The Derivatives of y = ln x
x
d d 1 1
dx
ln x = ∫ t dt = x
dx 1

BMM 104: ENGINEERING MATHEMATICS I Page 10 of
16

d 1
ln x = , x > 0
dx x

Generally, if u is a differentiable function of x whose values are positive, so that ln u is defined,
then applying the Chain Rule

dy dy du
=
dx du dx
to the function y = ln u gives

d d du 1 du
ln u = ln u =
dx du dx u dx

d 1 du
ln u = , u >0
dx u dx



Find the derivative of y with respect to x, t, or θ , as appropriate for the following functions.

1 + ln t
1. y = ln 3 x 16. y=
t
ln x
2. y = ln kx 17. y=
1 + ln x
x ln x
3. y = ln( t 2 ) 18. y=
1 + ln x
3
4. 19. y = ln(ln x )
y = ln( t 2 )
3
5. y = ln 20. y = ln(ln(ln x ))
x
10
6. y = ln 21. y = θ(sin(ln θ ) + cos(ln θ ))
x
7. y = ln( θ + 1 ) 22. y = ln(sec θ + tan θ )
1
8. y = ln( 2θ + 2 ) 23. y = ln
x x +1
1 1+ x
9. y = ln x 3 24. y = ln
2 1−x
1 + ln t
10. y = (ln x )3 25. y=
1 − ln t
11. y = t(ln t ) 2 26. y = ln t
12. y =t ln t 27. y = ln(sec(ln θ ))

16

x4 x4 sin θ cos θ
13. y= ln x − 28. y = ln( )
4 16 1 + 2 ln θ
x3 x3 ( x 2 + 1 )5
14. y= ln x − 29. y = ln( )
3 9 1− x
ln t ( x + 1 )5
15. y= 30. y = ln
t ( x + 2 ) 20


1 − ln t
1. 16.
x t2
1 1
2. 17.
x x( 1 + ln x ) 2
2 ln x
3. 18. 1−
t ( 1 + ln x ) 2
3 1
4. 19.
2t x ln x
1 1
5. − 20.
x x(ln x ) ln(ln x )
1
6. − 21. 2 cos(ln θ )
x
1
7. 22. sec θ
θ +1
1 − 3x + 2
8. 23.
θ +1 2 x( x + 1 )
3 1
9. 24.
x 1 − x2
3(ln x ) 2 2
10. 25.
x t( 1 − ln t ) 2
1
11. (ln t ) 2 + 2 ln t 26.
4t ln t
1
1 tan(ln θ )
12. (ln t )2 + 1 27.
θ
2(ln t ) 2

1 4 
13. x 3 ln x 28.
2cot θ − tan θ − θ ( 1 + 2 ln θ ) 

10 x 1
14. x 2 ln x 29. −
x + 1 2( 1 − x )
2

1 − ln t 5 3x + 2 
15. 30. − 
t2 2 ( x + 1 )( x + 2 ) 


The Derivative of e x

16

d x
e = ex
dx
d u du
e = eu
dx dx



Find the derivative of y with respect to x, t, or θ , as appropriate for the following functions.

1. y = e −5 x
2
x
2. y =e3
3. y = e 5− x
7

x +x 2 )
4. y = e( 4
5. y = xe x − e x
6. y = ( 1 + 2 x )e −2 x
7. y = ( x 2 − 2 x + 2 )e x
8. y = ( 9 x 2 − 6 x + 2 )e 3 x
9. y = eθ (sin θ + cos θ )
10. y = ln( 3θe −θ )
y = cos( e −θ )
2
11.
12. y = θ 3 e −2θ cos 5θ
13. y = ln( 3te −t )
14. y = ln( 2e −t sin t )
eθ
15. y = ln( )
1 + eθ
θ
16. y = ln( )
1+ θ
17. y = e (cos t +ln t )
18. y = e sin t (ln t 2 + 1 )

dy
Find .
dx

16

1. ln y = e y sin x 2. ln xy = e x +y
3. e 2 x = sin( x + 3 y ) 4. tan y = e e + ln x


1
1. −5e −5 x 10. −1
θ
2
2 3x
2θe −θ sin( e −θ )
2 2
2. e 11.
3
3. −7 e 5 −7 x 12. θ 2 e −2θ ( 3 cos 5θ − 2θ cos 5θ − 5θ sin 5θ )
2 x +x2 ) 1 −t
4. ( + 2 x )e ( 4 13.
x t
cos t − sin t
5. xe x 14.
sin t
1
6. −4 xe −2 x 15.
1 + eθ
1
7. x 2e x 16.
2θ ( 1 + θ 1 / 2 )
8. 27 x 2 e 3 x 17. ( 1 −t sin t )e cos t
 2
9. 2eθ cos θ 18. e sin t ln( t 2 + 1 )(cos t ) 
 t

dy
Find .
dx

ye y cos x 2e 2 x − cos( x + 3 y )
1. 3.
y
1 − ye sin x 3 cos( x + 3 y )
1
− e x +y ( xe x + 1 ) cos 2 y
2. y
4.
x

Monotonic Functions, the First Derivative and Second Derivative Test for Concavity and Curve
Sketching

Definitions: Increasing, Decreasing Function

Let f be a function defined on an interval I and let x1 and x 2 be any two points in I.

1. If f ( x1 ) < f ( x 2 ) whenever x 1 < x 2 , then f is said to be increasing on
I.
2. If f ( x1 ) > f ( x 2 ) whenever x 1 < x 2 , then f is said to be decreasing on
I.
A function that is increasing or decreasing on I is called monotonic on I.

16

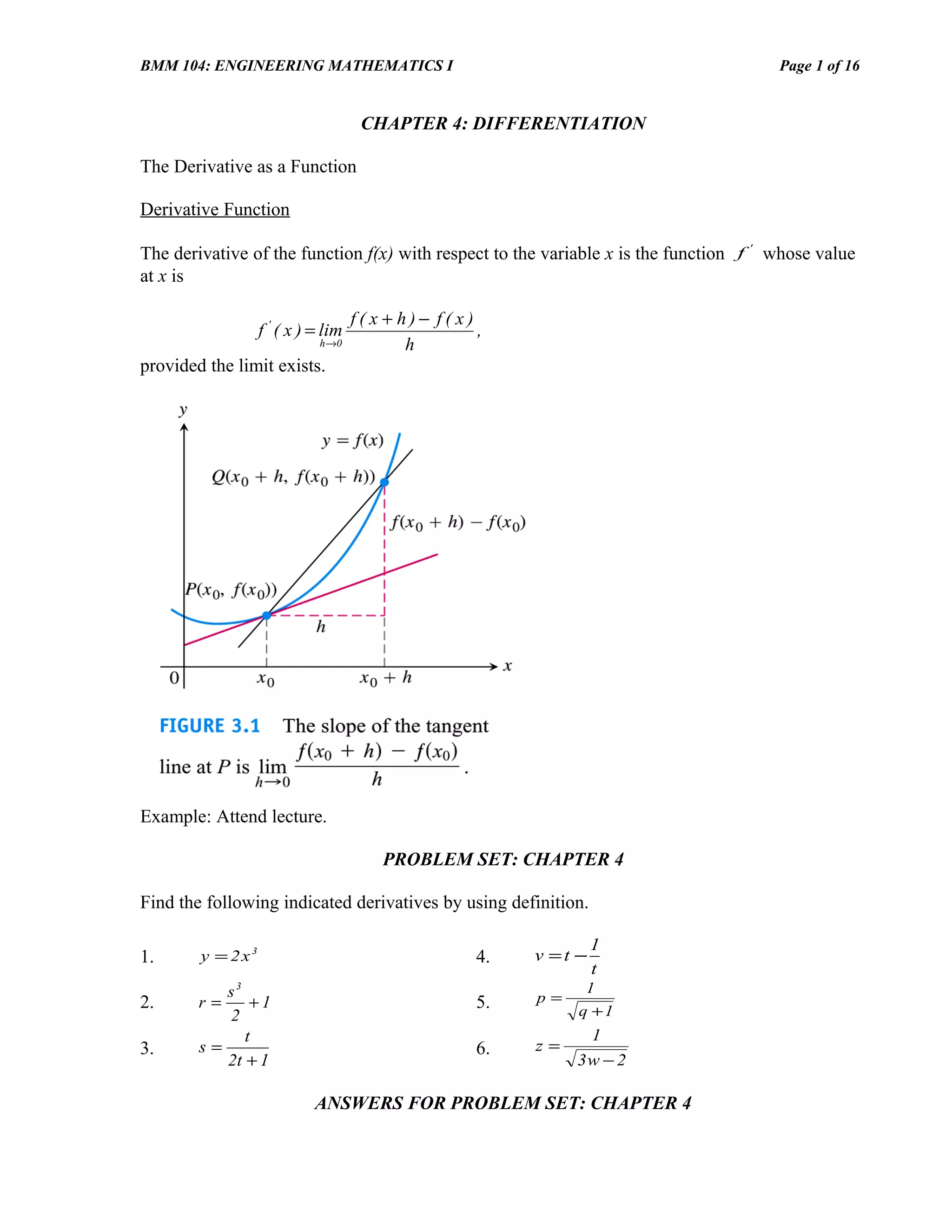
First Derivative Test for Monotonic Functions

Suppose that f is continuous on [a, b] and differentiable on (a, b).

If f ' ( x ) > 0 at each point x ∈( a ,b ) , then f is increasing on [a, b].
If f ' ( x ) < 0 at each point x ∈( a ,b ) , then f is decreasing on [a, b].

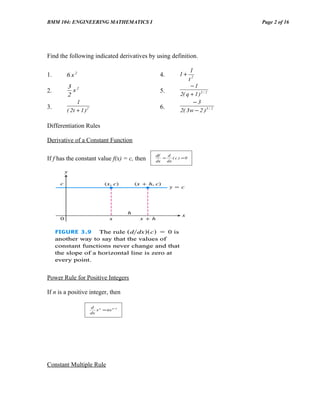
First Derivative Test for Local Extrema

Suppose that c is a critical point of a continuous function f, and that f is differentiable
at every point in some interval containing c expect possibly at c itself.
Moving across c from left to right.

1. if f ' changes from negative to positive at c, then f has a local minimum at
c;
2. if f ' changes from positive to negative at c, then f has a local maximum
at c;
3. if f ' does not change sign at c (that is, f ' is positive on both sides of c
or negative on both sides), then f has no local extremum at c.

16

The Second Derivative Test for Concavity

Let y = f(x) be twice-differentiable on an interval I.
1. If f '' > 0 on I, the graph of f over I is concave up.
2. If f '' < 0 on I, the graph of f over I is concave down.

Definition: Point of Inflection

A point where the graph of a function has a tangent line and where the concavity
changes is a point of inflection.

Inflection point

Second Derivative Test for Local Extrema

Suppose f is continuous on an open interval that contains x = c.
''

1. If f ' ( c ) = 0 and f '' ( c ) < 0 , then f has a local maximum at x = c.
2. If f ' ( c ) = 0 and f '' ( c ) > 0 , then f has a local minimum at x = c.
3. If f ' ( c ) = 0 and f '' ( c ) = 0 , then the test fails. The function f may have a
local maximum, a local minimum, or neither.

16

Graph Sketching

Strategy for Graphing y = f(x)
1. Identify the domain of f and any symmetries the curve may have.
2. Find y ' and y '' .
3. Find the critical points of f, and identify the function’s behavior at each one.
4. Find where the curve is increasing and where it is decreasing.
5. Find the points of inflection, if any occur, and determine the concavity of the
curve.
6. Identify any asymptotes.
7. Plot key points, such as the intercepts and the points found in Steps 3-5, and
sketch the curve.

Example: Attend lecture


Sketch the graph for the following functions.

1. y = 2 x 3 − 3 x 2 − 12 x + 5
2. y = x 3 + 6 x 2 − 15 x
3. y = 27 x − x 3
x3
4. y= + x 2 − 3x + 7
3
3x 2 x3
5. y = 1 + 4x − −
2 3


Solution: Attend lecture.

Chapter 4(differentiation)

More Related Content

What's hot

Similar to Chapter 4(differentiation)

Recently uploaded

Chapter 4(differentiation)