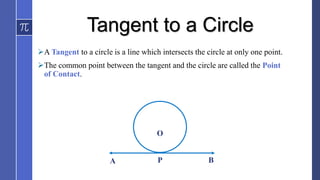
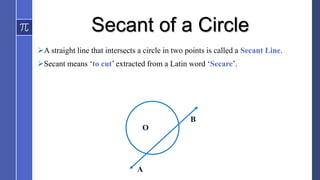
The document covers topics related to circles, including definitions of tangents and secants, along with key theorems and proofs such as the perpendicularity of tangents to radii and the equality of lengths of tangents from an external point. Several important theorems regarding circle geometry and exercises to illustrate these concepts are included. Examples demonstrate how to apply these theorems in practical problems involving circle properties.

1. CIRCLES
Class – 10th

2. Topics to be Covered
Tangent To A Circle
Secant Of A Circle
Theorem 10.1
Theorem 10.2
Important Theorems
Examples
Exercise 10.1
Exercise 10.2

3. Tangent to a Circle
A Tangent to a circle is a line which intersects the circle at only one point.
The common point between the tangent and the circle are called the Point
of Contact.
A B
P
O

4. Secant of a Circle
A straight line that intersects a circle in two points is called a Secant Line.
Secant means ‘to cut’ extracted from a Latin word ‘Secare’.
A
B
O

5. Theorem 10.1
Statement:-Tangent at any point of the circle is
perpendicular to the radius through the point of
contact.
Given:- A circle with center O & XY is a tangent to
a circle at point P.
To Prove:- OP is perpendicular to XY.
Construction:- Take a point on Q on XY and join
OQ.
Proof:- As, OQ > OP
Hence, OP is the shortest distance to join XY.
OP is perpendicular to XY.
P
X
Y
O
Q

6. Theorem 10.2
Statement:- Lengths of tangents drawn from an external point to
circle are equal.
Given:- A circle with center O & PQ and PR are tangents to the
circle from point P.
To Prove:- PQ = PR
Construction:- Join OQ, OR & OP.
Proof:- Now, in ∆OQP and ∆ORP:
 OQ = OR (Radii of the circle)
 OP = OP (Common)
 OQP = ORP (Th. 10.1)
, ∆OQP  ∆ORP (RHS)
Hence, PQ = PR (CPCT)
O
Q
P
R

7. Important Theorems
 Tangents drawn at the ends of a diameter of a circle are
parallel.
 The perpendicular at the point of contact to the tangent to a
circle passes through the center.
 The angle between the two tangents drawn from an external
point to a circle is supplementary to the angle, subtended by
the line-segment joining the points of contact at the center.
 The opposite sides of a quadrilateral circumscribing a circle
subtend supplementary angles, at the center of the circle.
 In two concentric circles, the chord of the larger circle,
which touches the smaller circle, is bisected at the point of
contact.

8. EXAMPLES
1. Prove that in two concentric circles, the chord of larger circle, which touches
the smaller circle, is bisected at the point of contact.
Ans. Given:- Two concentric circles C1 and C2 with centre O. AB is the chord for
larger circle and tangent for smaller circle.
To Prove:- AP = BP
Construction:- Join OP.
Proof:- Now, AB is tangent to C2.
 OP  AB (Th. 10.1)
Now, AB is a chord of the circle C1.
 OP is  bisector of AB.
Hence, AP = BP.

9. 2. Two tangents TP and TQ are drawn to a circle with center O from an external
point T. Prove that ∠PTQ = 2∠OPQ.
Ans. Given:- TP and TQ are tangents to the circle with center O.
To Prove:- ∠PTQ = 2∠OPQ
Construction:- Join OP and OQ.
Proof:- Now, TP = TQ (Th. 10.2). So, ∆TPQ is isosceles.
∠TPQ = ∠TQP =
1
2
(180°- ∠PTQ) = 90°-
1
2
∠PTQ
Also, ∠OPT = 90°.
So, ∠OPQ = ∠OPT – ∠TPQ = 90°- [90°-
1
2
∠PTQ]
=
1
2
∠PTQ
This gives, ∠PTQ = 2∠OPQ
Hence, proved.
O
P
T
Q

10. 3. PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P
and Q intersect at a point T. Find the length TP.
Ans. Construction:- Join OT. Let it intersect PQ at R.
Proof:- As, TP = TQ (Th. 10.2)
, ∆TPQ is isosceles.
TO is the angle bisector of ∠ PTQ. OT is  bisector of PQ. , PR = RQ = 4 cm
By Pythagoras Theorem,  OR = OP2 − PR2= 52 − 42 = 3cm.
Now, in ∆TRP and ∆PRO:-
∠TRP = ∠PRO (90)
 ∠TPR = ∠POR (Angle in alternate segment)
, ∆TRP  ∆PRO (AA rule)

TP
P0
=
RP
RO
⇒
TP
4
=
5
3
⇒ TP =
20
3
cm.