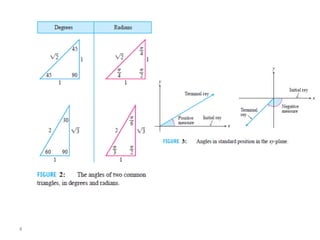
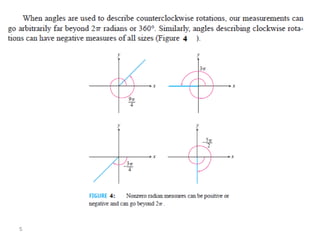
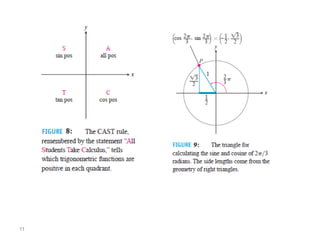
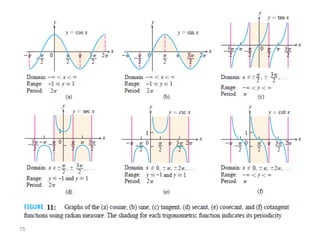
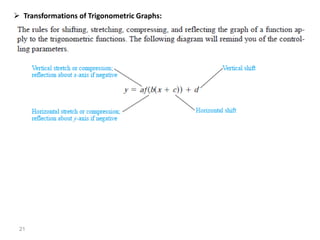
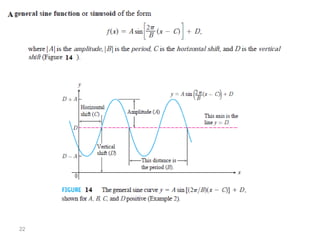
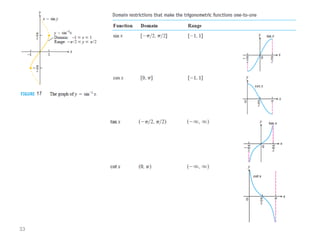
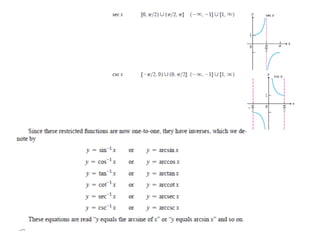
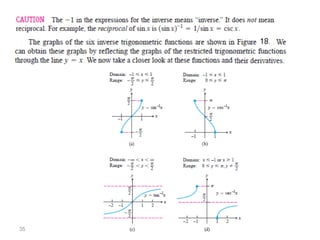
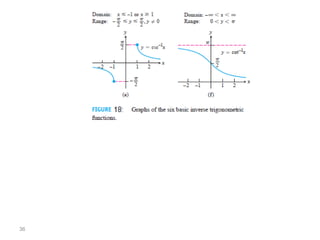
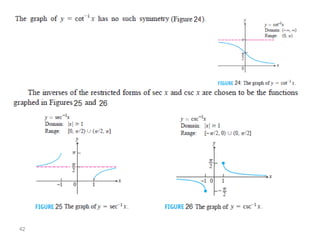
The document covers various aspects of trigonometric functions, including their definitions, periodicity, identities, and the law of cosines. It also discusses the derivatives of both basic and inverse trigonometric functions, providing examples and applications in calculus. Additionally, integration formulas related to trigonometric functions are mentioned along with exercises for practice.

1. Trigonometric Functions

2. Trigonometric Functions:
Radian Measure
2

3. 3

4. 4

5. 5

6. 6

7. The Six Basic Trigonometric Functions:
7

8. 8

9. 9

10. 10

11. 11

12. 12

13. 13

14.  Periodicity and Graphs of the Trigonometric Functions:
14

15. 15

16. 16

17. 17
Identities:

18. 18

19. 19

20. 20
 The Law of Cosines:

21. 21
 Transformations of Trigonometric Graphs:

22. 22

23. 23
Derivatives of Trigonometric Functions:
 Derivative of the Sine Function

24. 24

25. 25
EXAMPLE 1: Derivatives Involving the Sine

26. 26
 Derivative of the Cosine Function: (H.W. deriving)
EXAMPLE 2 : Derivatives Involving the Cosine

27. 27
EXAMPLE 3 : Motion on a Spring

28. 28

29. 29
 Derivatives of the Other Basic Trigonometric Functions:

30. 30
EXAMPLE 4:

31. 31
EXAMPLE 5:
EXAMPLE 6: Finding a Trigonometric Limit

32. 32
Inverse Trigonometric Functions
Inverse trigonometric functions arise when we want to calculate angles from side
measurements in triangles. They also provide useful antiderivatives and appear
frequently in the solutions of differential equations.
 Defining the Inverses

33. 33

34. 34

35. 35

36. 36

37. 37
 The Arcsine and Arccosine Functions

38. 38

39. 39

40. 40
 Identities Involving Arcsine and Arccosine

41. 41
 Inverses of tan x, cot x, sec x, and csc x

42. 42

43. 43

44. 44

45. 45

46. 46
The Derivative of y=sin-1u

47. 47

48. 48

49. 49
EXAMPLE 6: Applying the Derivative Formula:
The Derivative of y=tan-1u:

50. 50
EXAMPLE 7: A Moving Particle:

51. 51
The Derivative of y=sec-1u (derivation H.W)
EXAMPLE 8: Using the Formula

52. 52
Derivatives of the Other Three
We could use the same techniques to find the derivatives of the other three inverse
trigonometric functions—arccosine, arccotangent, and arccosecant—but there is a
much easier way, thanks to the following identities.

53. 53
The derivatives of the inverse trigonometric functions are summarized in Table 7.3.

54. 54
 Integration Formulas

55. 55
EXAMPLE 10: Using the Integral Formulas

56. 56
EXAMPLE 11: Using Substitution and Table 2

57. 57
EXAMPLE 13: Completing the Square
Evaluate

58. 58
EXAMPLE 14: Using Substitution
Evaluate
EXERCISES: 7.7 H.W