This document defines and provides examples of B-trees, which are multi-way search trees used to store data in databases. B-trees allow for fast searches, insertions, and deletions. The key points are:
1. B-trees are m-way trees where each node can have up to m children. They maintain sorted keys and partition data to keep leaves at the same level.
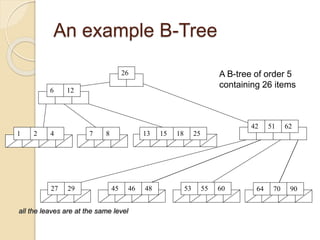
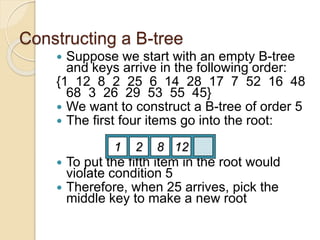
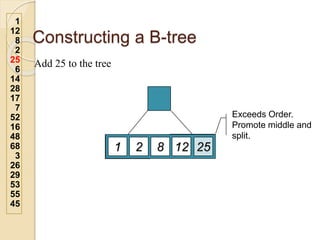
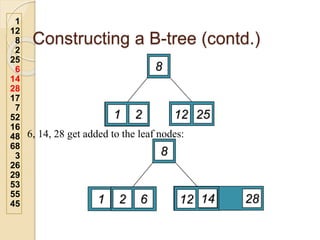
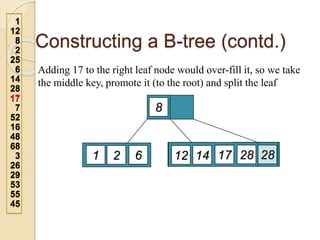
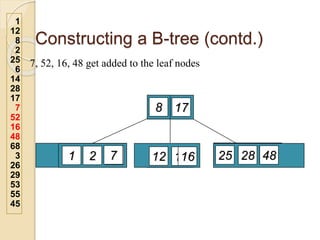
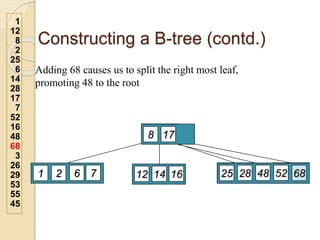
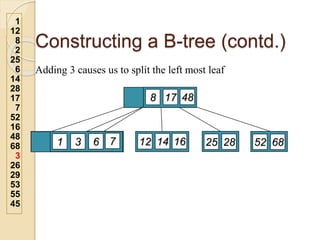
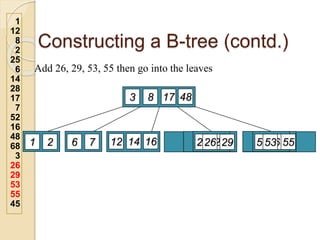
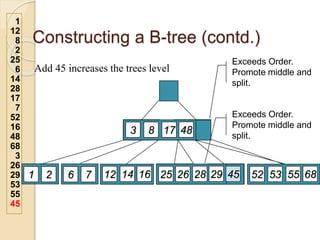
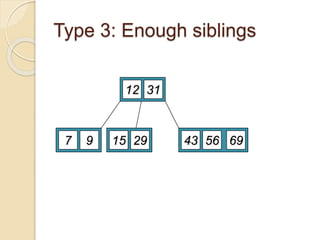
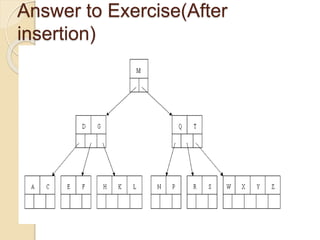
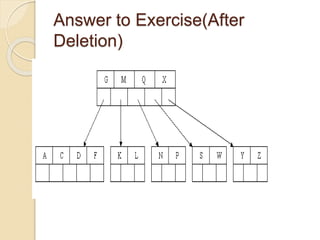
2. An example demonstrates a 5-way B-tree containing 26 items. The process of constructing a B-tree by inserting keys one by one is also shown step-by-step.
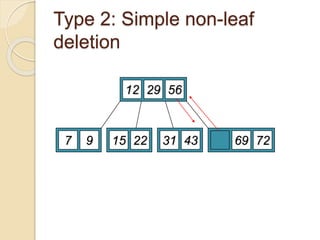
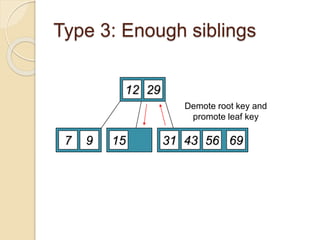
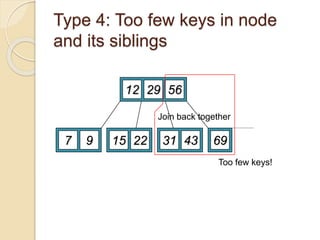
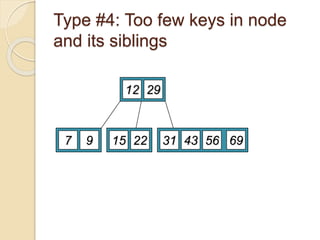
3. Deletion from a B-tree can involve removing a key from a leaf, borrowing/prom