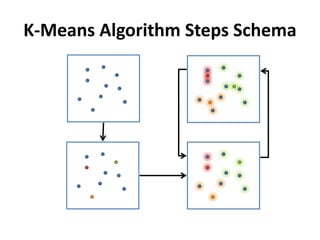
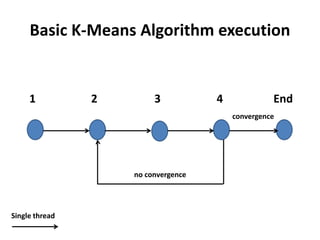
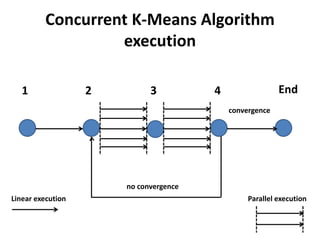
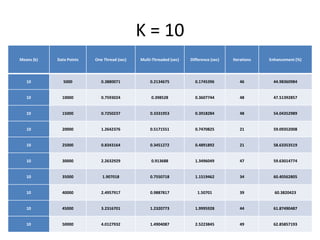
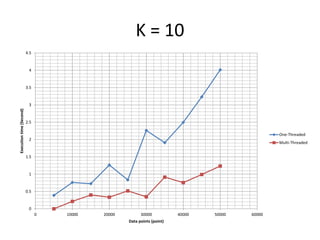
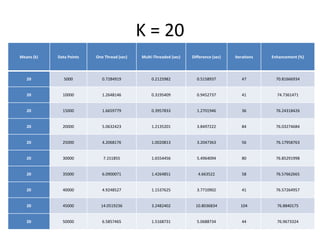
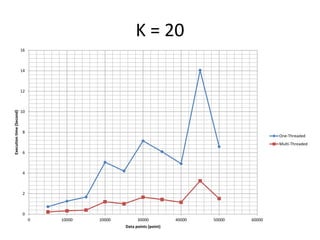
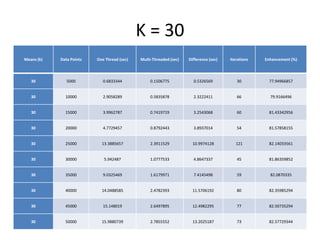
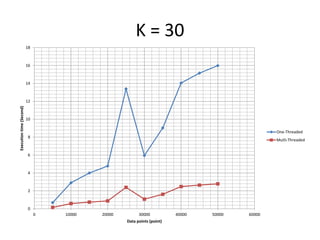
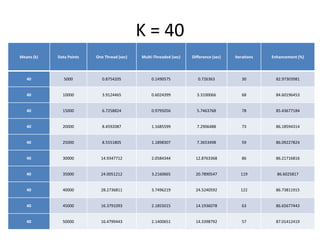
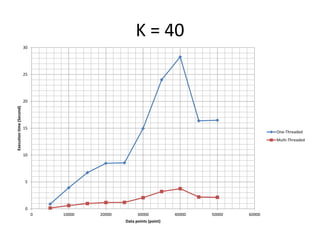
The document discusses enhancing the K-Means clustering algorithm performance by converting it to a concurrent version using multi-threading. It identifies that steps 2 and 3 of the basic K-Means algorithm contain independent sub-tasks that can be executed in parallel. The implementation in C# uses the Parallel class to parallelize the processing. Analysis shows the concurrent version runs 70-87% faster with increasing performance gains at higher numbers of clusters and data points. Future work could parallelize the full K-Means algorithm.

1. Enhancing the performance of
K-Means algorithm

2. Plan
• Basic K-Means Algorithm
• Converting basic K-Means algorithm to
concurrent
• Implementation of K-Means algorithm using
C#
• Analysis of Results
• Conclusion

3. Basic K-Means Algorithm

4. Definition
• K-Means clustering is a method of cluster
analysis which aims to partition n
observations into k clusters in which each
observation belongs to the cluster with the
nearest mean.

5. Definition
• The K-Means problem is to find cluster centers
that minimize the sum of squared distances
from each data point being clustered to its
cluster center (the center that is closest to it).
• A very common measure is the sum of
distances or sum of squared Euclidean
distances from the mean of each cluster.

6. Basic K-Means
Algorithm Steps

7. Step 1
The algorithm arbitrarily selects k
points as the initial cluster centers
(“means”).

8. Step 2
Each point in the dataset is assigned to
the closed cluster, based upon the
Euclidean distance between each point
and each cluster center.

9. Step 3
Each cluster center is recomputed as
the average of the points in that
cluster.
Steps 2 and 3 repeat until the clusters converge.

10. Convergence
Convergence means that either no
observations change clusters when
steps 2 and 3 are repeated or that the
changes do not make a material
difference in the definition of the
clusters

11. K-Means Algorithm Steps Schema

12. K-Means Algorithm Deficiencies
• The k-means algorithm has at least two major
theoretic shortcomings:
It has been shown that the worst case running
time of the algorithm is super-polynomial in the
input size.
The approximation found can be arbitrarily bad
with respect to the objective function compared
to the optimal clustering.

13. Our Work
Basic K-Means will be updated and
manipulated to a Concurrent K-Means
version that uses special .Net framework
libraries to take advantage of Multi-
threading Technology.

14. Our Work
This Concurrent version of K-Means
reserves all the benefits of Basic K-Means
and adds to it a much faster and
manipulated abilities that makes the
software runs as fast as 70%~85% more
than Basic K-Means.

15. Converting Basic K-Means
algorithm into Concurrent

16. First Step
First we must identify the Task
containing independent sub-tasks
that can be executed in parallel.

17. Identifying sub-Tasks
Consider the K-Means algorithm as follows:
1) Pick Random Center Points
2) Assign Points To Centers
3) Calculate New Centers
4) Check If Centers Are Equal
(if so, quit Else Go to 2)

18. Basic K-Means Algorithm execution
1 2 3 4 End
no convergence
convergence
Single thread

19. Identifying sub-Tasks
In step 2, we are going to loop over every
point and determine which center is
closest to it. Since there is no state
modified during this lookup.
we can easily make this processes parallel.

20. Identifying sub-Tasks
In step 3, when we calculate new centers,
we are just going to loop over all of the
points in a given group and calculate their
“average” location (or centroid)

21. Identifying sub-Tasks
The Steps 2 and 3 are the best steps that
we can apply parallelism on them because
they are composed of independent loops
executed over the data points.

22. Concurrent K-Means Algorithm
execution
Linear execution
1 2 3 4 End
Parallel execution
no convergence
convergence

23. Implementation of K-Means
algorithm using C#

24. Basic K-Means algorithm
For step 3, all we need to do is loop through
each point and check every center until we find
the closest one.
If we weren’t concerned with writing a parallel
application then we could simple loop over
them with a normal foreach statement:
foreach (var point in Points){ //content goes here }

25. Concurrent K-Means algorithm
But if we leverage the
System.Threading.Tasks.Parallel class in .NET 4.0, we
could simply write this:
Parallel.ForEach(points, point =>
{ //contents goes here });
The same thing is repeated in step 4

26. Demo Application

27. Application Snapshots

28. Application Snapshots

29. Analysis of Results

30. Used machine
• Experiments are made under the following
machine:
• CPU = Intel(R) Xeon(R) X5690 @ 3.47 GHz/ 63.9
Gb of RAM
• Operating System = Microsoft Windows Server
2003 Enterprise X64 Edition Service Pack 2
• Number of Processors = 24
• Application Type = 64 bit

31. K = 10
Means (k) Data Points One Thread (sec) Multi-Threaded (sec) Difference (sec) Iterations Enhancement (%)
10 5000 0.3880071 0.2134675 0.1745396 46 44.98360984
10 10000 0.7593024 0.398528 0.3607744 48 47.51392857
10 15000 0.7250237 0.3331953 0.3918284 48 54.04352989
10 20000 1.2642376 0.5171551 0.7470825 21 59.09352008
10 25000 0.8343164 0.3451272 0.4891892 21 58.63353519
10 30000 2.2632929 0.913688 1.3496049 47 59.63014774
10 35000 1.907018 0.7550718 1.1519462 34 60.40562805
10 40000 2.4957917 0.9887817 1.50701 39 60.3820423
10 45000 3.2316701 1.2320773 1.9995928 44 61.87490487
10 50000 4.0127932 1.4904087 2.5223845 49 62.85857193

32. 0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
0 10000 20000 30000 40000 50000 60000
Executiontime(Second)
Data points (point)
One-Threaded
Multi-Threaded
K = 10

33. K = 20
Means (k) Data Points One Thread (sec) Multi-Threaded (sec) Difference (sec) Iterations Enhancement (%)
20 5000 0.7284919 0.2125982 0.5158937 47 70.81666934
20 10000 1.2648146 0.3195409 0.9452737 41 74.7361471
20 15000 1.6659779 0.3957833 1.2701946 36 76.24318426
20 20000 5.0632423 1.2135201 3.8497222 84 76.03274684
20 25000 4.2068176 1.0020813 3.2047363 56 76.17958763
20 30000 7.151855 1.6554456 5.4964094 80 76.85291998
20 35000 6.0900071 1.4264851 4.663522 58 76.57662665
20 40000 4.9248527 1.1537625 3.7710902 41 76.57264957
20 45000 14.0519236 3.2482402 10.8036834 104 76.8840175
20 50000 6.5857465 1.5168731 5.0688734 44 76.9673324

34. K = 20
0
2
4
6
8
10
12
14
16
0 10000 20000 30000 40000 50000 60000
Executiontime(Second)
Data points (point)
One-Threaded
Multi-Threaded

35. K = 30
Means (k) Data Points One Thread (sec) Multi-Threaded (sec) Difference (sec) Iterations Enhancement (%)
30 5000 0.6833344 0.1506775 0.5326569 30 77.94966857
30 10000 2.9058289 0.5835878 2.3222411 66 79.9166496
30 15000 3.9962787 0.7419719 3.2543068 60 81.43342956
30 20000 4.7729457 0.8792443 3.8937014 54 81.57858155
30 25000 13.3885657 2.3911529 10.9974128 121 82.14033561
30 30000 5.942487 1.0777533 4.8647337 45 81.86359852
30 35000 9.0325469 1.6179971 7.4145498 59 82.0870335
30 40000 14.0488585 2.4782393 11.5706192 80 82.35985294
30 45000 15.148019 2.6497895 12.4982295 77 82.50735294
30 50000 15.9880739 2.7855552 13.2025187 73 82.57729344

36. K = 30
0
2
4
6
8
10
12
14
16
18
0 10000 20000 30000 40000 50000 60000
Executiontime(Second)
Data points (point)
One-Threaded
Mutli-Threaded

37. K = 40
Means (k) Data Points One Thread (sec) Multi-Threaded (sec) Difference (sec) Iterations Enhancement (%)
40 5000 0.8754205 0.1490575 0.726363 30 82.97303981
40 10000 3.9124465 0.6024399 3.3100066 68 84.60196453
40 15000 6.7258824 0.9795056 5.7463768 78 85.43677184
40 20000 8.4592087 1.1685599 7.2906488 73 86.18594314
40 25000 8.5551805 1.1898307 7.3653498 59 86.09227824
40 30000 14.9347712 2.0584344 12.8763368 86 86.21716816
40 35000 24.0051212 3.2160665 20.7890547 119 86.6025817
40 40000 28.2736811 3.7496219 24.5240592 122 86.73811915
40 45000 16.3791093 2.1855015 14.1936078 63 86.65677443
40 50000 16.4799443 2.1400651 14.3398792 57 87.01412419

38. K = 40
0
5
10
15
20
25
30
0 10000 20000 30000 40000 50000 60000
Executiontime(Second)
Data points (point)
One-Threaded
Multi-Threaded

39. Results Analysis
• In case of K = 10, the results show that when
data points number is 5000 the algorithm is
enhanced by 44.98360984 % and this value
grows up to reach 62.85857193 % when data
points number is 50000 .

40. Results Analysis
• In case of K = 20, the results show that when
data points number is 5000 the algorithm is
enhanced by 70.81666934 % and this value
grows up to reach 76.9673324 % when data
points number is 50000 .

41. Results Analysis
• In case of K = 30, the results show that when
data points number is 5000 the algorithm is
enhanced by 77.94966857 % and this value
grows up to reach 82.57729344 % when data
points number is 50000 .

42. Results Analysis
• In case of K = 40, the results show that when
data points number is 5000 the algorithm is
enhanced by 82.97303981 % and this value
grows up to reach 87.01412419 % when data
points number is 50000.

43. Results Analysis
• If we regress the enhancement (Y) on the
number of means (X1) and the data points
(X2) we will have the equation below:
• Enhancement = 49.762 + 0.871 (Number of
means) + 0.0001 (Number of data points)
• R2 = 0.83251942

44. Conclusion

45. Conclusion
• This equation shows that there are a high
correlation between the Enhancement and
the number of means. We can say that when
the number of means is bigger, the
enhancement is better. We have this result
because we used parallel loops when looping
over clusters. So multi-threading is used more
when we have more means.

46. Future Work
In this project we have worked only on two tasks
in the K-Means algorithm (Steps 2 & 3).
In future works, we can work on converting the
whole algorithm into concurrent.