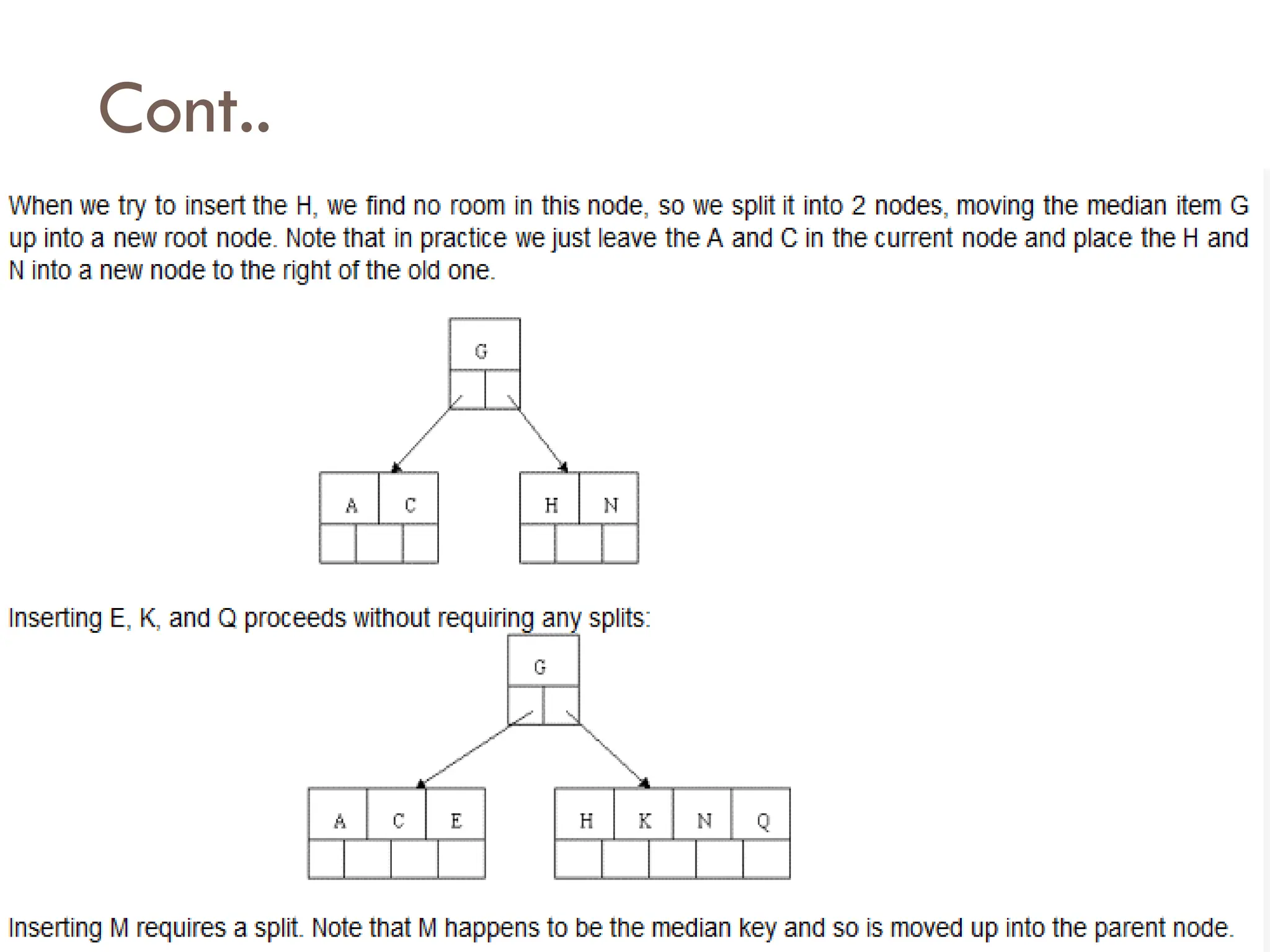
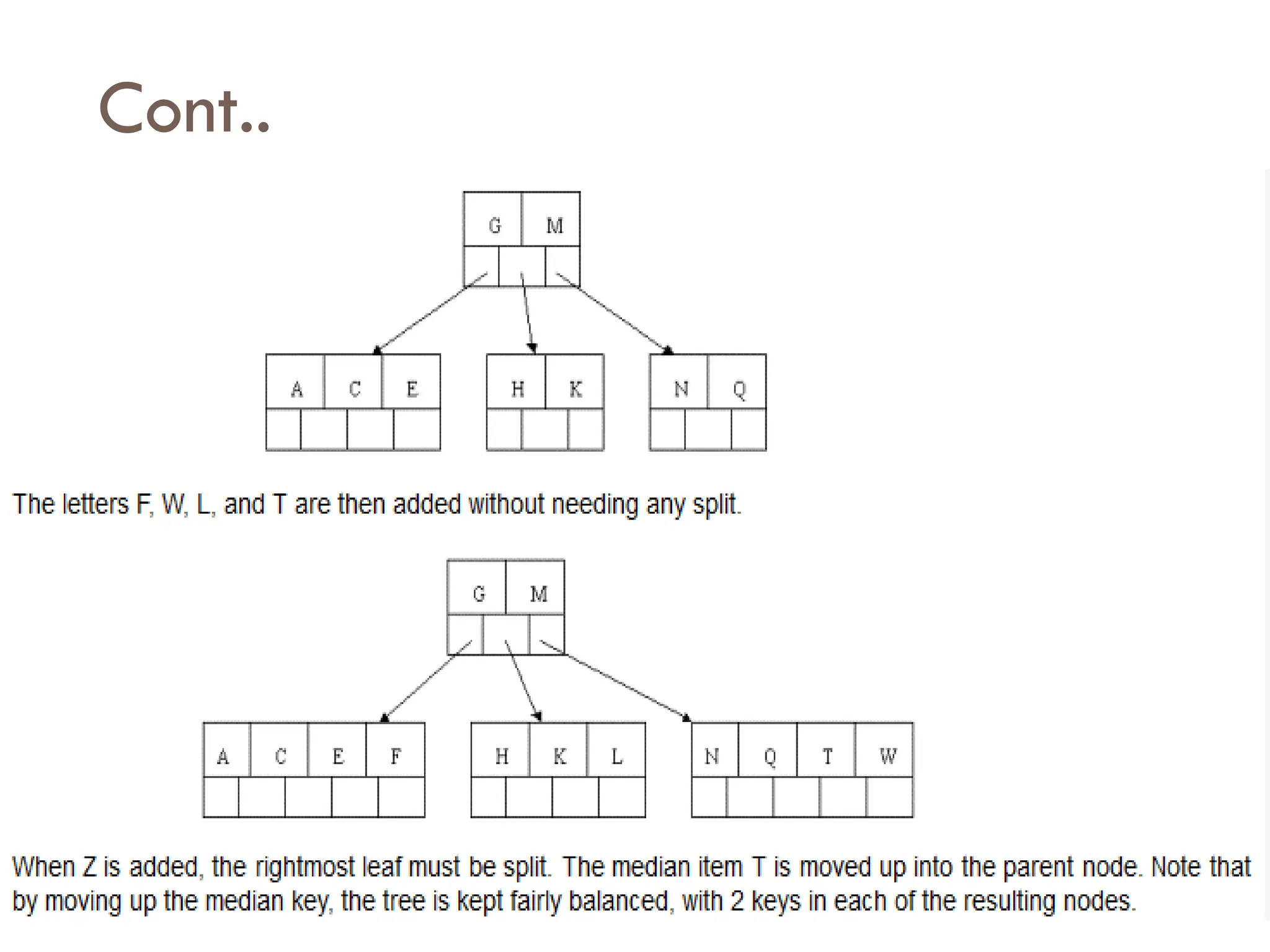
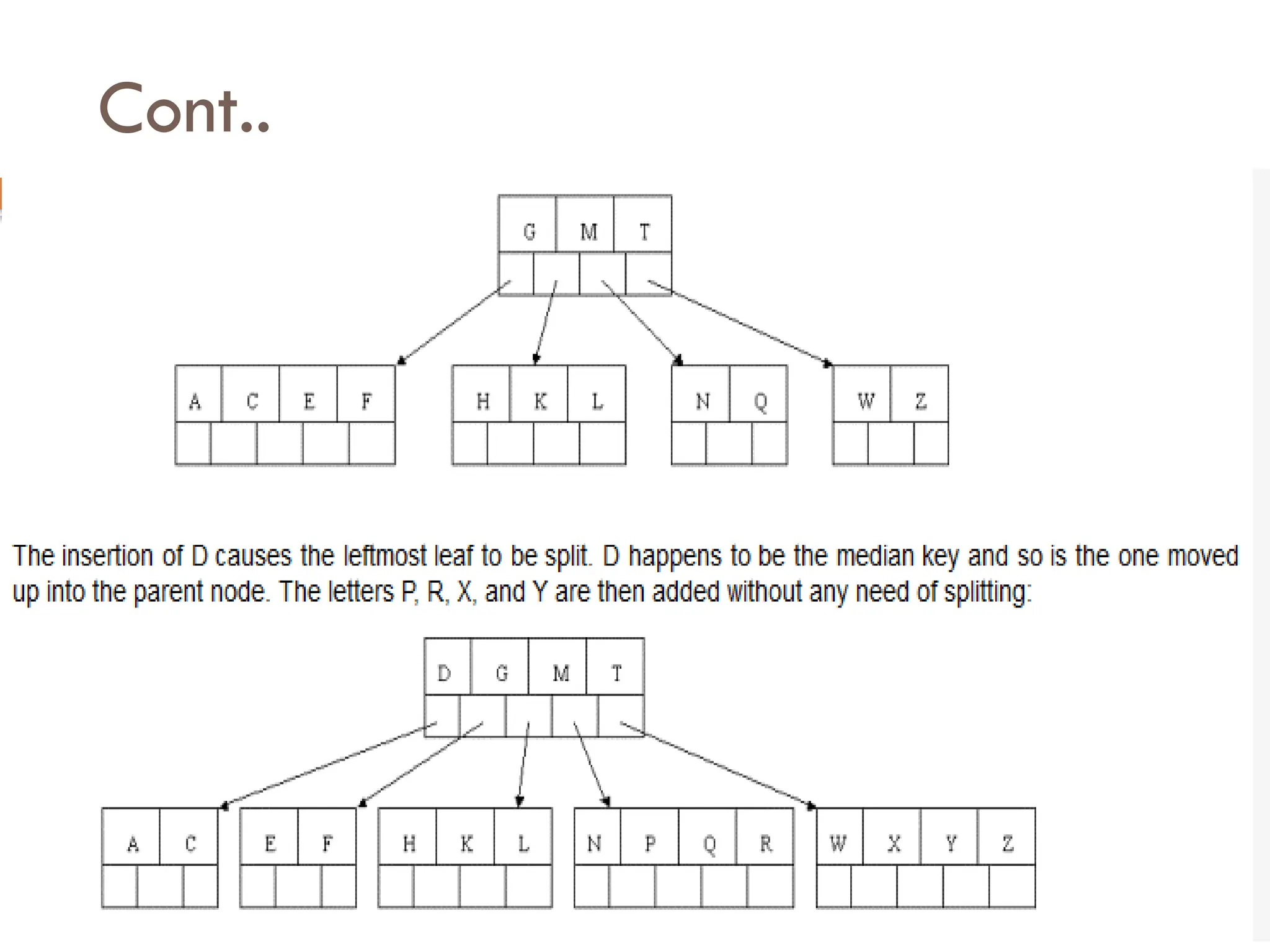
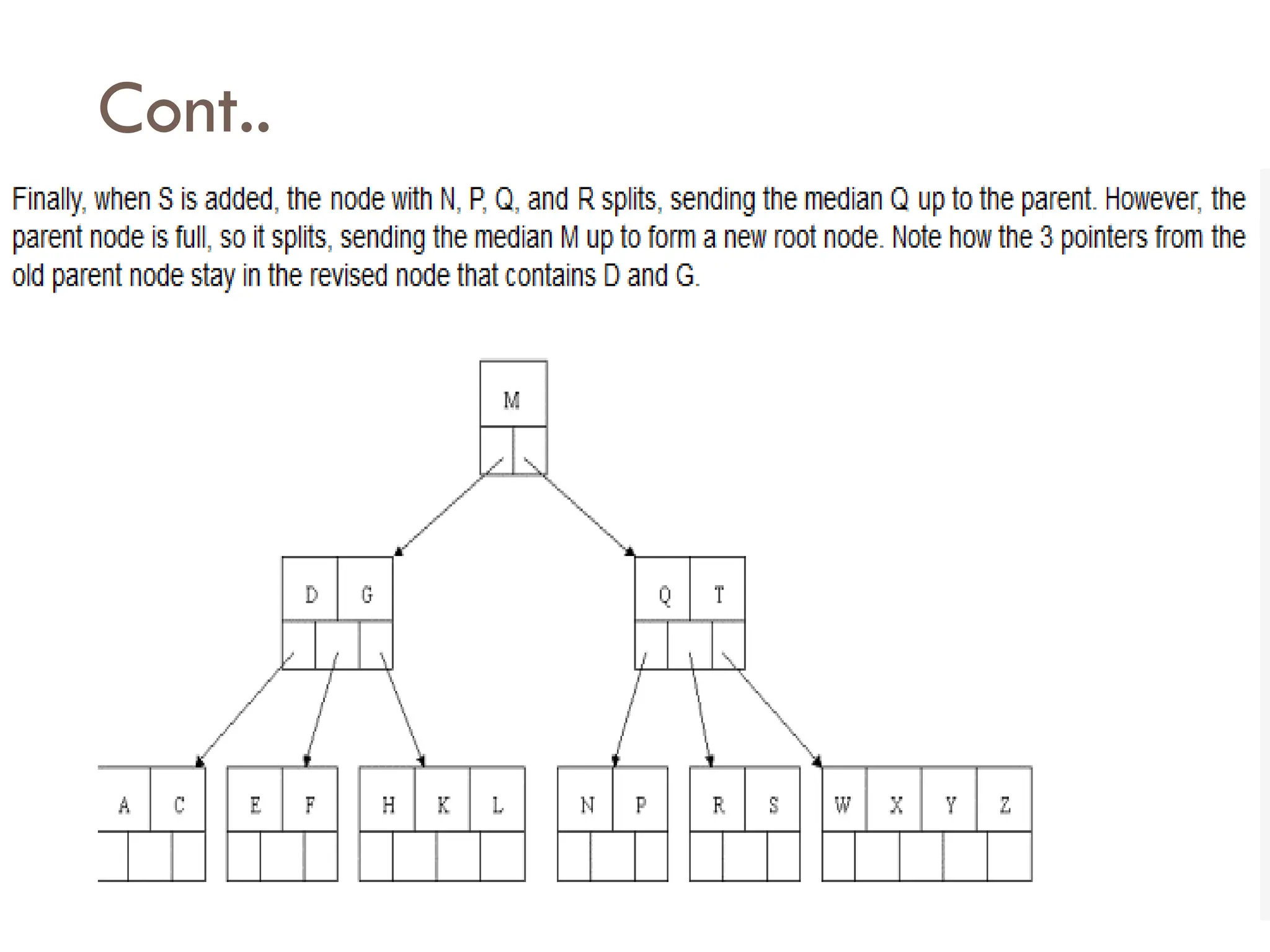
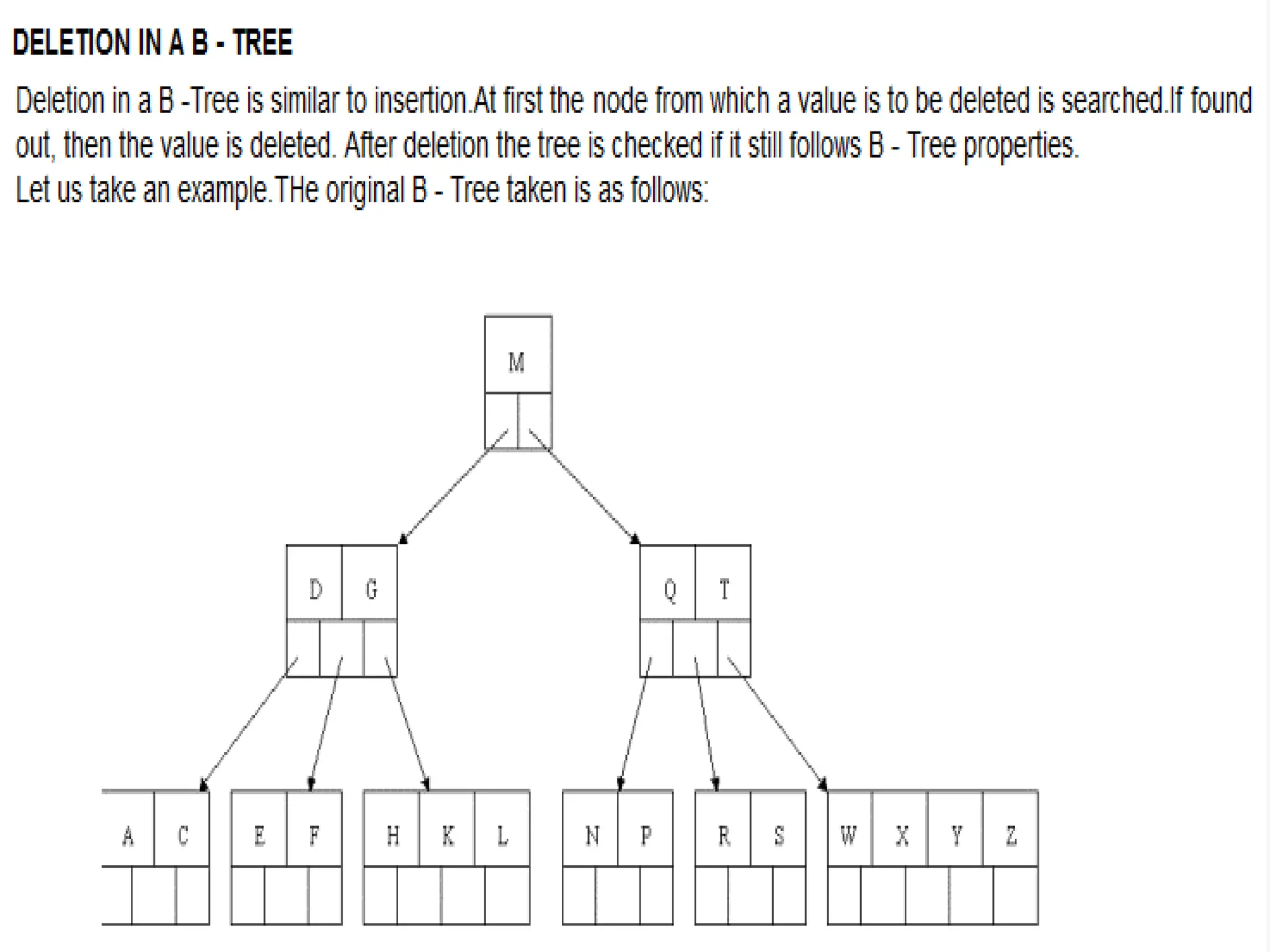
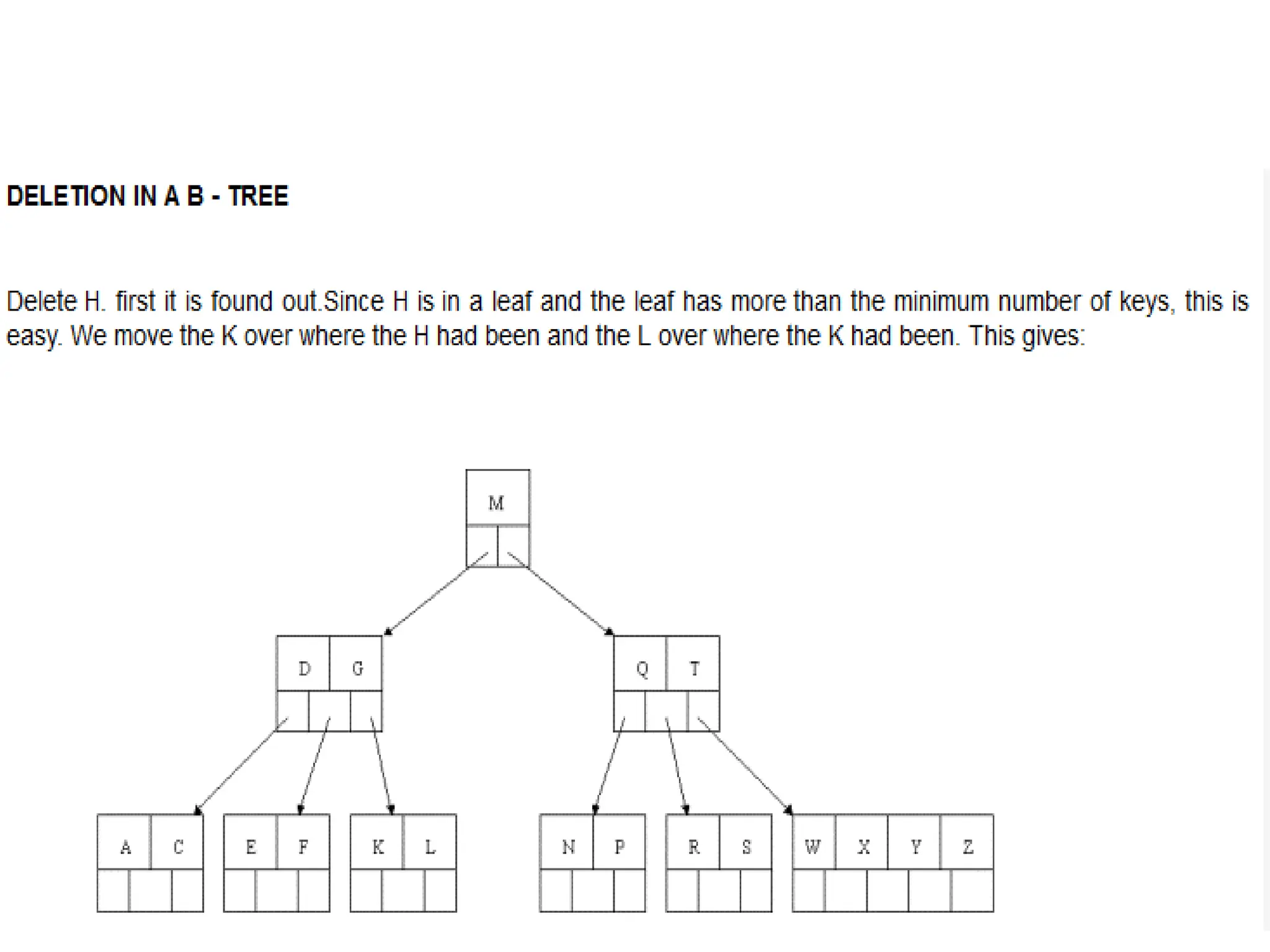
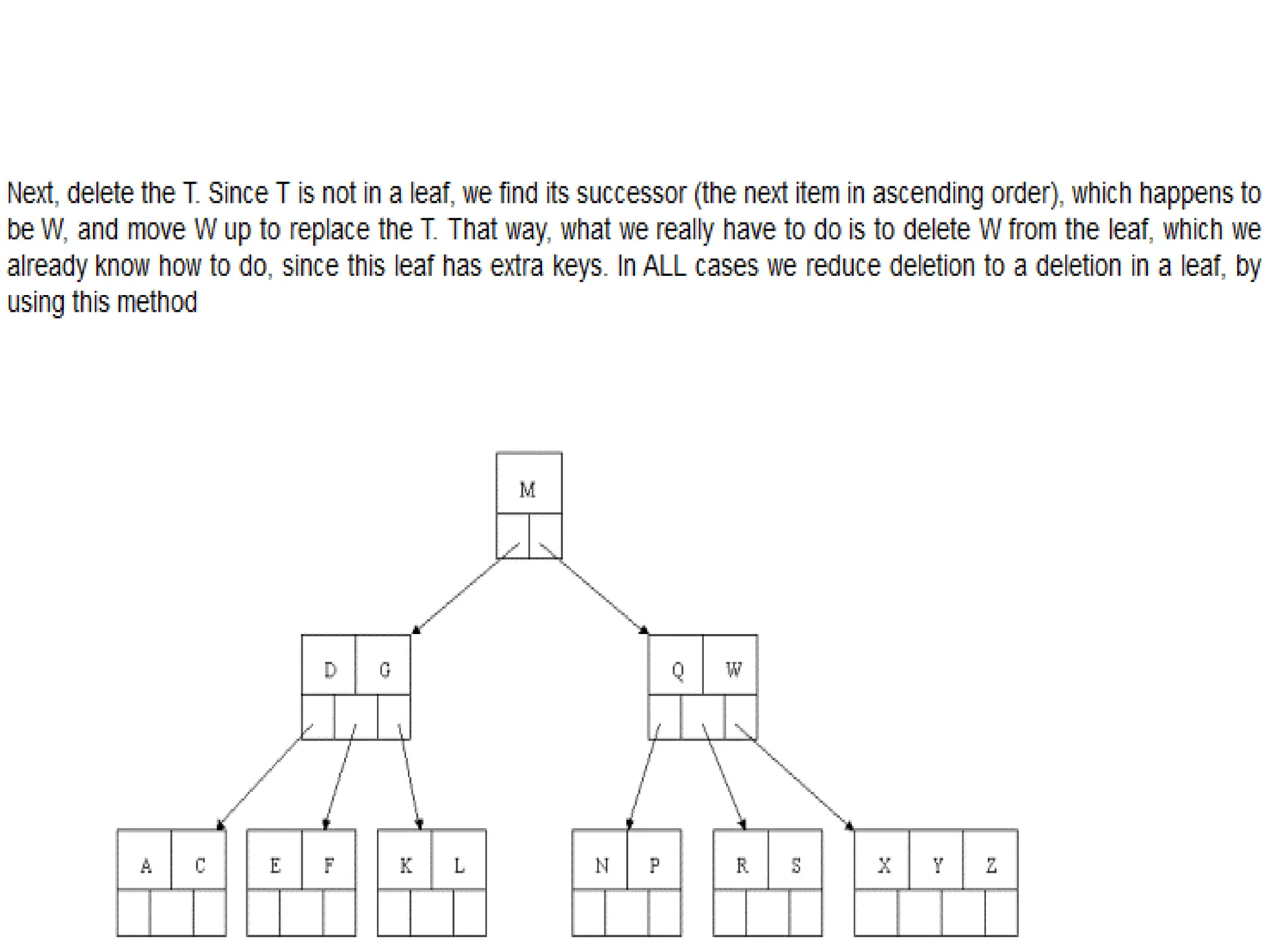
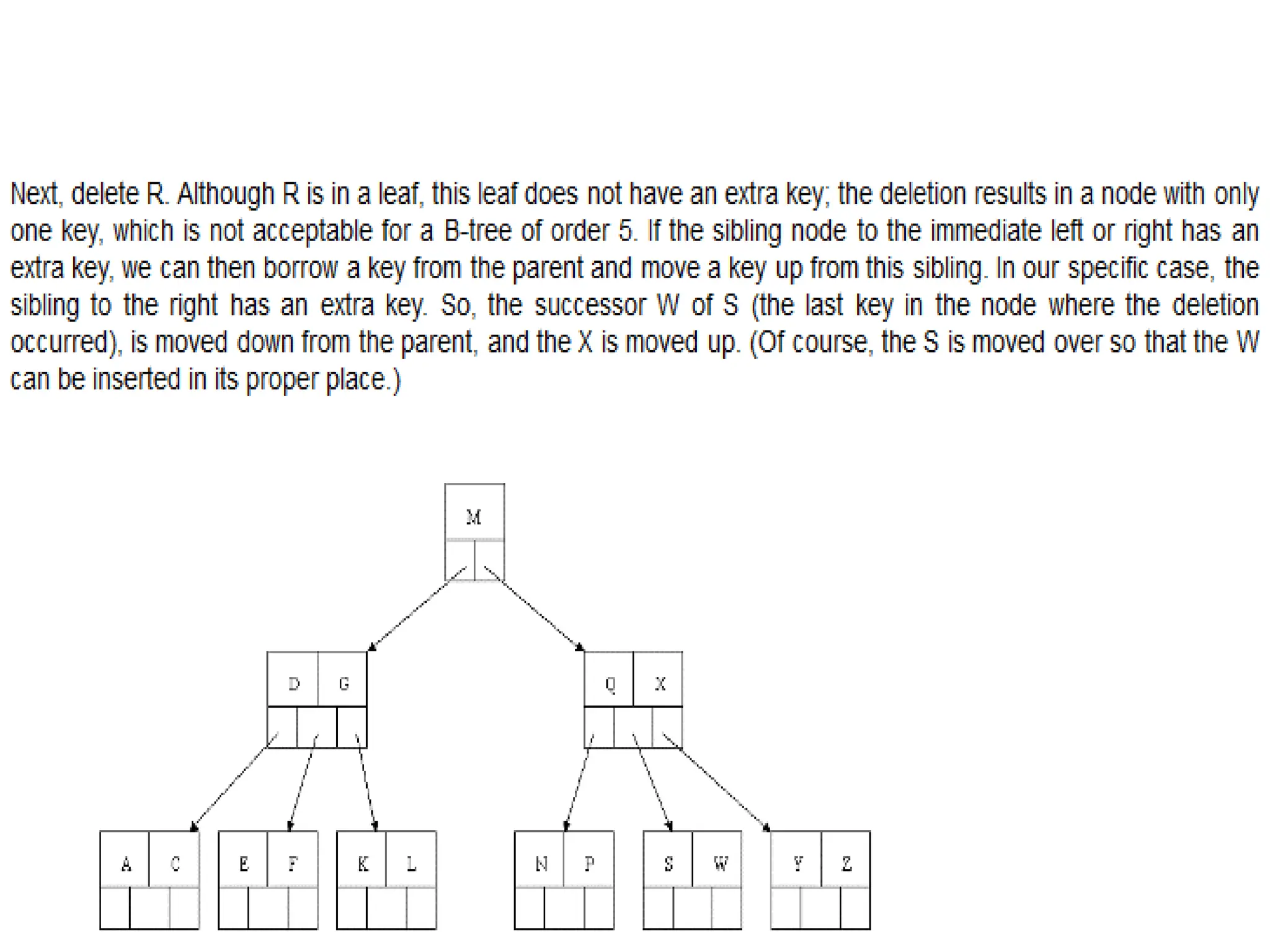
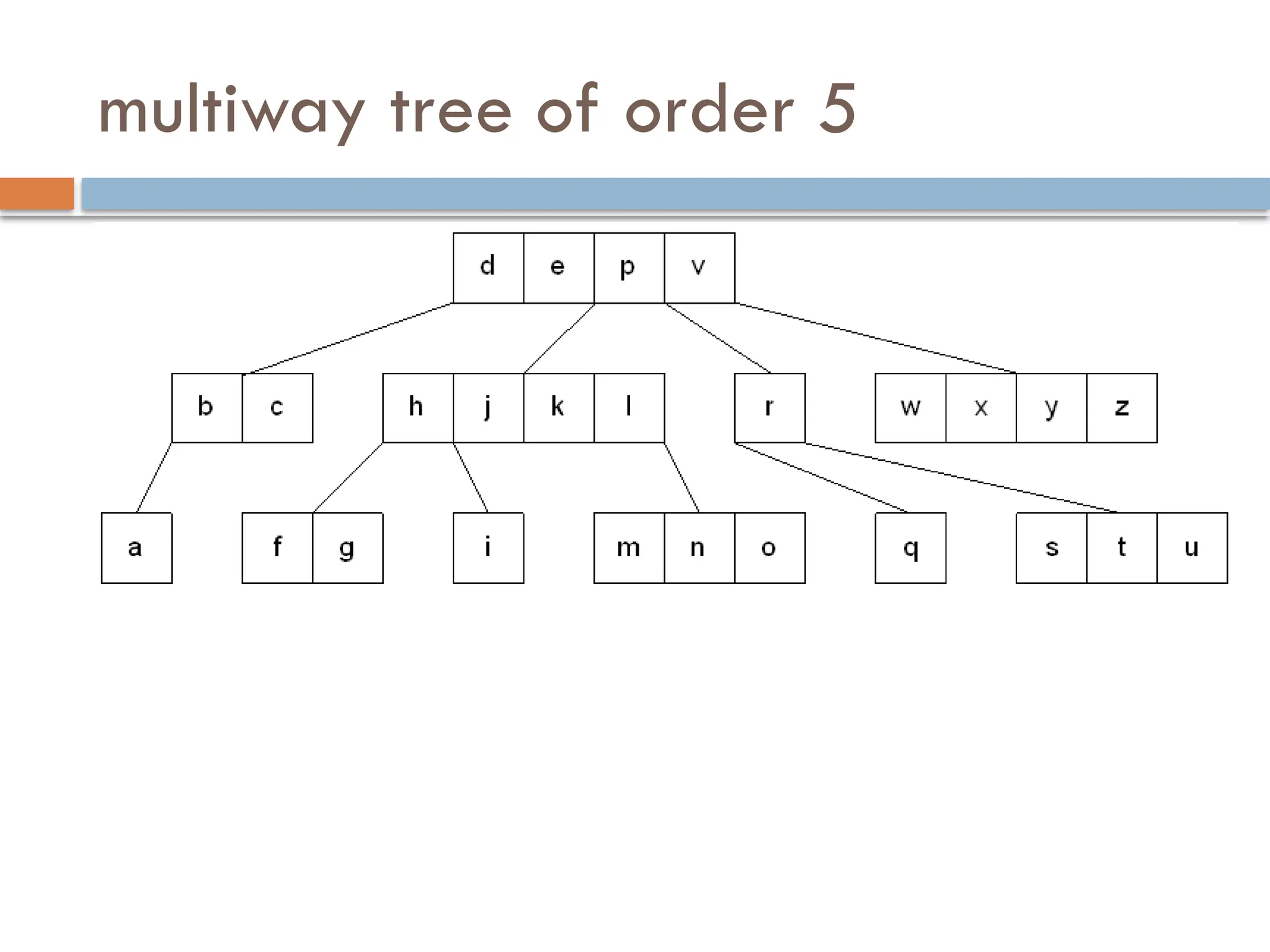
The document explains m-way search trees, which are multiway trees allowing nodes to have multiple children and keys stored in ascending order, enhancing search operations compared to binary trees. It details properties and algorithms for searching within m-way trees and describes B-trees, a type of balanced m-way tree with specific structural rules that optimize data retrieval from secondary storage. Examples of creating B-trees with various orders illustrate the application of these concepts.

1. M-WAY SEARCH TREE

2. Multiway Search Tree
 A binary search tree has one value in each node
and two subtrees.
 A multiway tree is a tree that can have more than
two children. A multiway tree of order m (or an m-
way tree) is one in which a tree can have m
children.
 M is the order of the tree.

3. multiway tree of order 5

4. Properties
 By definition an m-way search tree is a m-way tree
in which:
 Each node has m children and m-1 key fields
 The keys in each node are in ascending order.
 The key of the data entries are ordered as
key1<=key2<=<=key3………………..<keyk
 All subtree are them seleves multiway trees.
 The keys in the first i children are smaller than the i th key
 The keys in the last m-i children are larger than the i th
key

5. Example
 Here is a 3-way search tree:
 The algorithm for searching for a value in an M-way search
tree is the obvious generalization of the algorithm for
searching in a binary search tree.

6. Searching in M way tree
 If we are searching for value X are and currently at
node consisting of values V1...Vk, there are four
possible cases that can arise:
 If X < V1, recursively search for X in V1's left subtree.
 If X > Vk, recursively search for X in Vk's right subtree.
 If X=Vi, for some i, then we are done (X has been found).
 the only remaining possibility is that, for some i, Vi < X <
V(i+1). In this case recursively search for X in the subtree
that is in between Vi and V(i+1).

7.  M way tree used to reduce the height of the tree
 M way tree is not balanced tree.
 An extension of a multiway search tree of order m
is a B-tree of order m.

8. B tree
 To reduce the time lost in retrieving data from secondary storage,
we need to minimize the no. of references to the secondary memory.
 This is possible if a node in a tree contains more no. of values, then
in a single reference to the secondary memory more nodes can be
accessed.
 The AVL trees or red Black Trees can hold a max. of 1 value only in
a node while 2-3 Trees can hold a max of 2 values per node.
 To improve the efficiency Multiway Search Trees are used.

9. Properties
 A B Tree of order n is a Multiway Search Tree of order n with the
following characteristics:
 All the non leaf nodes have a max of n child nodes & a min of n/2 child
nodes.
 If a root is non leaf node, then it has a max of n non empty child nodes &
a min of 2 child nodes.
 If a root node is a leaf node, then it does not have any child node.
 A node with n child nodes has n-1 values arranged in ascending order.
 All values appearing on the left most child of any node are smaller than
the left most value of that node while all values appearing on the right
most child of any node are greater than the right most value of that node.
 If x & y are two adjacent values in a node such that x < y, ie they are the
i th & (i+1) th values in the node respectively, then all values in the (i+1) th
child of that node are > x but < y.

10.  A B-tree is an M-way search tree with two special
properties:
 It is perfectly balanced: every leaf node is at the same
depth.
 Every node, except perhaps the root, is at least half-
full, i.e. contains M/2 or more values (of course, it
cannot contain more than M-1 values). The root may
have any number of values (1 to M-1).
 The 3-way search tree above is clearly not a B-tree.
Here is a 3-way B-tree containing the same values:

11. Example

12. Operations
 THE following operations can be done on a B - Tree :
 Searching
 Insertion
 Deletion

13. SEARCHING OF A VALUE IN A B-TREE
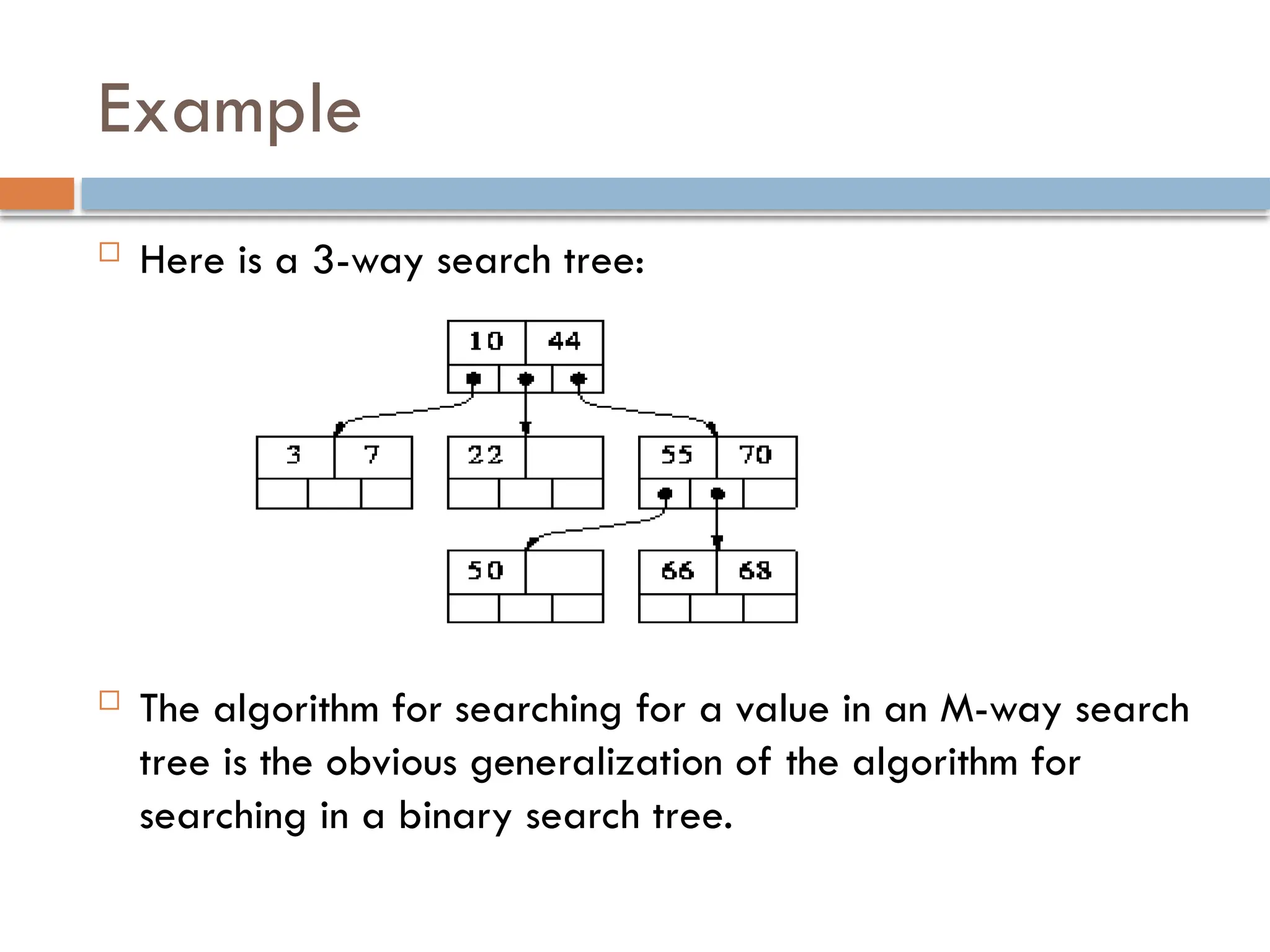
 Searching of a value k in a B-Tree is exactly similar to
searching for values in a 2-3 tree.
 To begin with the value k is compared with the first
value key [0] of the root node.
 If they are similar then the search is complete.
 If k is less than key [0] then the search is done in the
first child node or the sub-tree of the root node.

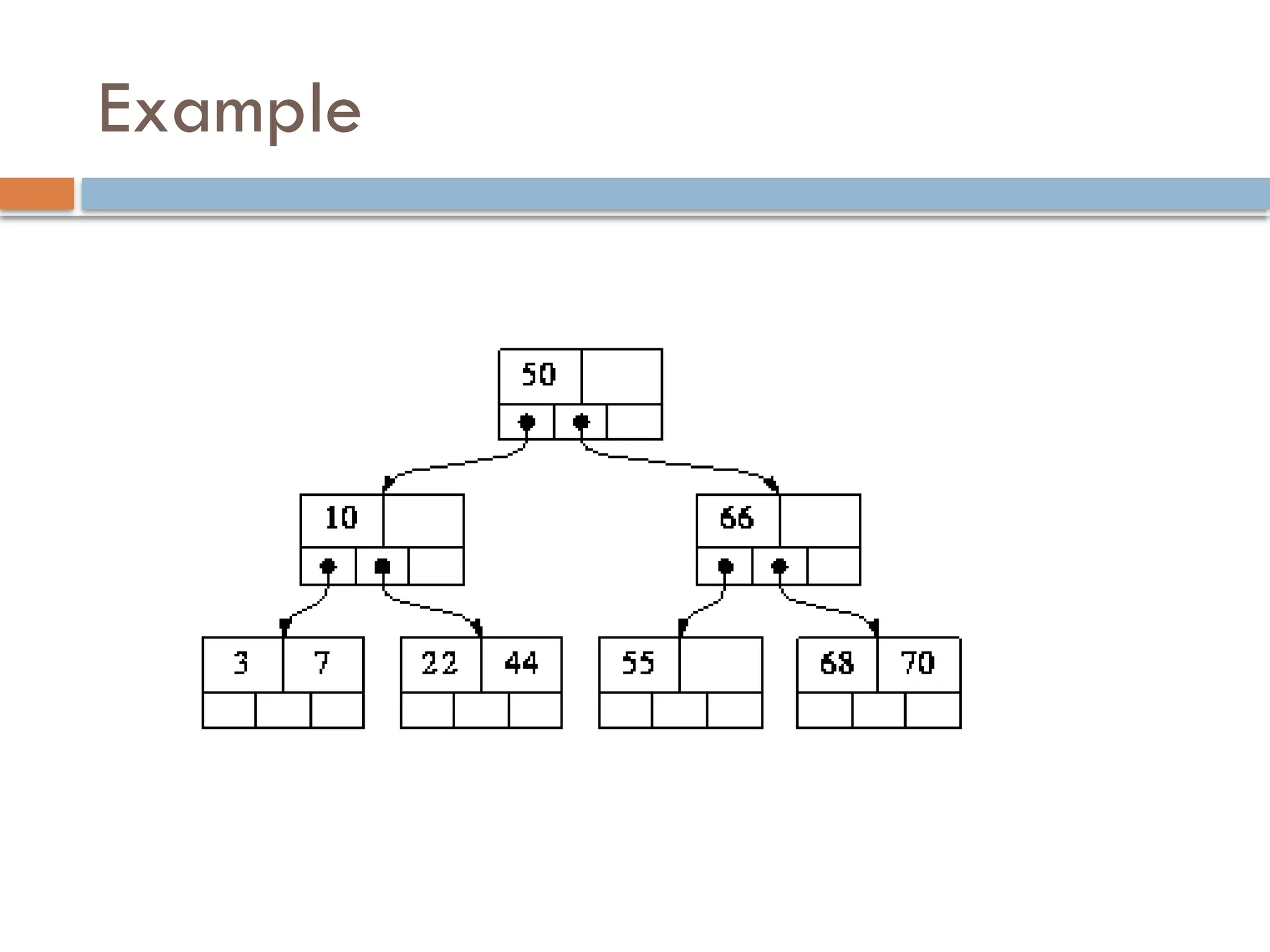
14. Cont..
 If k is greater than key [0] then it is compared with key [1]. If k
is greater than key [0] and smaller than key [1] then k is
searched in the second child node or sub-tree of the root node.
 If k is greater than the last value key [i] of the root node then
searching is done in the last child node or sub-tree of the root
node.
 If k is searched in any of the child nodes or sub-tree of the
root node then the same procedure of searching is repeated
for that particular node or sub-tree.

15. Cont..
 If the value k is found in the tree then the search is
successful .
 The address of the node in which k is present and
the position of the value k in that node is returned.
 If the value k is not found in the tree, then the
search is unsuccessful

17. Cont..

18. Cont..

19. Cont..

20. Cont..

27. Example of B tree Creation
 Create a b tree of order 5 for following sequence
 3, 14, 7, 1, 8, 5, 11, 17, 13, 6, 23, 12, 20, 26, 4, 16, 18, 24, 25, 19
 Create a b tree of order 4 for following sequence
 92, 24, 6, 7, 11, 8, 22, 4, 5, 16, 19, 20, 78
 Create a b tree of order 5 for following sequence
 92, 24, 6, 7, 11, 8, 22, 4, 5, 16, 19, 20, 78
 Create a b tree of order 3 for following sequence
 20, 10, 30, 15, 12, 40, 50
 Create a b tree of order 3 for following sequence
 5, 3, 21, 9, 1, 13, 2, 7, 10, 12, 4, 8