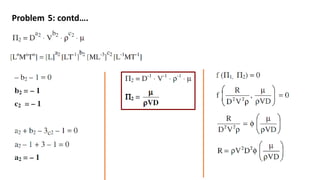
This document discusses dimensional analysis and similitude. It defines dimensional analysis as the study of relations between physical quantities based on their units and dimensions. Dimensional analysis involves identifying the base quantities like length, mass, time that physical quantities are measured in. Dimensional analysis is useful for checking equations for dimensional homogeneity and developing scaling laws. The document discusses Rayleigh's and Buckingham π theorem methods of dimensional analysis. It also discusses the three types of similitude required for model analysis: geometric, kinematic and dynamic similitude. Finally, it defines several common dimensionless numbers like Reynolds number, Froude number, Euler number, Weber number and Mach number in terms of dominant forces.

1. Dimensional Analysis &
Similitude
Dr. Vijay G. S.
Professor
Dept. of Mech. & Ind. Engg.
MIT, Manipal
email: vijay.gs@manipal.edu
Mob.: 9980032104

2. What is Dimensional Analysis ??
• Dimensional analysis is the study of the relation between physical
quantities based on their units and dimensions.
• It is the analysis of the relationships between different physical
quantities by identifying their base quantities (such as length, mass,
time, etc.) and units of measure (such as miles versus kilometres, or
pounds versus kilograms)

3. Dimension and Units
• Dimension: A measure of a physical quantity .
• Unit: A way to assign a number to that dimension.
• There are seven primary dimensions called as fundamental or basic
dimensions.
• Mass, Length, Time, Temperature, Electric current, amount of light,
and amount of matter.

4. Fundamental Dimensions

5. Fundamental Dimensions:
• All physical quantities are measured by comparison which is made with
respect to a fixed value.
• Length, Mass and Time are three fixed dimensions which are of
importance in fluid mechanics and fluid machinery.
• In compressible flow problems, temperature is also considered as a
fundamental dimensions.
Secondary Quantities or Derived Quantities:
• Secondary quantities are derived quantities or quantities which can be
expressed in terms of two or more fundamental quantities.

6. Dimensions of Various Quantities

7. The law of dimensional homogeneity:
• Every additive term in an equation must have the same dimensions.
• In an equation if each and every term or unit has same dimensions,
then it is said to have Dimensional Homogeneity.
Equation V = u + at 𝒑
𝝆𝒈
+
𝑽𝟐
𝟐𝒈
+ 𝒛 = 𝑪
Units m/s = m/s + (m/s2 )*s
𝑵
𝒎𝟐
𝒌𝒈
𝒎𝟑 ×
𝒎
𝒔𝟐
+
𝒎𝟐
𝒔𝟐
𝒎
𝒔𝟐
+ 𝒎 = 𝑪
Dimensions LT-1 = LT-1 + (LT-2) (T)
 LT-1 = LT-1 + LT-1
𝑴𝑳𝑻−𝟐
𝑳𝟐
𝑴
𝑳𝟑 ×
𝑳
𝑻𝟐
+
𝑳
𝑻
𝟐
𝑳
𝑻𝟐
+ 𝑳 = 𝑳

8. Uses of Dimensional Analysis:
 It is used to test the dimensional homogeneity of any derived equation.
 To predict trends in the relationship between parameters.
 To generate non dimensional parameters that help in the design of
experiments.
 To obtain scaling laws so that prototype performance can be predicted
from model performance.
 To develop a meaningful and systematic way to perform an experiment.
 Dimensional products are important and useful in planning, execution
and interpretation of experiments.

9. Methods of Dimensional Analysis
There are two methods of dimensional analysis.
1. Rayleigh’s method
2. Buckingham’s  – theorem method

10. • Let x1 is a function of x2, x3, x4, ……, xn.
• x1 is the dependent variable and x2, x3, …. xn are the independent variables.
• Then it can be written as, x1 = f (x2, x3, x4, ……, xn)
x1= K (x2
a .x3
b .x4
c .……)
• Writing dimensions for all the quantities
[LMT of x1] = [LMT of x2]a [LMT of x3]b [LMT of x4]c……
• Using the concept of Dimensional Homogeneity a, b, c …. can be
determined.
• Then, x1 = K ×⋅x2
a ×⋅x3
b ×⋅x4
c ……
1. Rayleigh’s method
• Rayleigh’s method of analysis is adopted when number of parameters
or variables are less. For instance 3 or 4 or 5.

11. Numerical problems on Rayleigh’s method:
Problem 1: Velocity of sound C in air varies as bulk modulus of elasticity K and the
mass density ρ. Derive an expression for the velocity in form 𝐶 =
𝐾
𝜌

12. Problem 2: Find the equation for the power P developed by a pump if it
depends on head H discharge Q and specific weight  of the fluid.

13. Problem 3: Find an expression for drag force R on a smooth sphere of diameter
D moving with uniform velocity V in a fluid of density ρ and dynamic viscosity µ.

14. Problem 4: The efficiency of a fan depends on the density ρ, dynamic
viscosity µ, angular velocity ω, diameter D, discharge Q. Express
efficiency in terms of dimensionless parameters using Rayleigh’s Method.

15. • This method of analysis is used when number of variables are more.
• It states that, if there are n – variables in a physical phenomenon and those
n-variables contain ‘m’ dimensions, then the variables can be arranged
into (n-m) dimensionless groups called  terms.
• If f (x1, x2, x3, ……… xn) = 0 and variables can be expressed using m
dimensions then, F(1, 2, 3, ……… n - m) = 0
• where, 1, 2, 3, ……… are dimensionless groups.
• Each  term contains (m + 1) variables out of which m are of repeating type
and one is of non-repeating type.
• Each  term is dimensionless
• Dimensional homogeneity can be used to get each  term.
2. Buckingham- Theorem

16. Selecting Repeating Variables:
1. Avoid taking the dependent variable (quantity required) as the repeating
variable.
2. Repeating variables put together should not form dimensionless group.
3. No two repeating variables should have same dimensions.
4. Repeating variables can be selected from each of the following properties.
• Geometric property  Length, height, width, area
• Flow property  Velocity, Acceleration, Discharge
• Fluid property  Mass density, Viscosity, Surface tension

17. Problem 5: Using the Buckingham- theorem, find an expression for drag force
R on a smooth sphere of diameter D moving with uniform velocity V in a fluid
of density ρ and dynamic viscosity µ.

18. Problem 5: contd….

19. Problem 6: The efficiency of a fan depends on density ρ, dynamic
viscosity µ, angular velocity ω, diameter D and discharge Q. Using
Buckingham’s- theorem, express efficiency in terms of dimensionless
parameters.
Comparing powers of T
-b1 - 1 = 0  b1 = -1
Comparing powers of M
c1 + 1 = 0  c1 = -1
Comparing powers of L
(1) Evaluating 1:

20. Problem 6: contd….
(2) Evaluating 2:
Comparing powers of M
Comparing powers of T
Comparing powers of L

21. Problem 6: contd….
(3) Evaluating 3:

22. Problem 7: Using the Buckingham’s- theorem, derive an expression for thrust
P developed by a propeller assuming that it depends on angular velocity ω,
speed of advance V, diameter D, dynamic viscosity µ, mass density ρ,
elasticity of the fluid medium which can be denoted by speed of sound in the
medium C.
No. of variables, n = 7
No. of dimensions, m = 3
No. of  terms = n – m = 7 – 3 = 4
Evaluating 1:
Comparing powers of T Comparing powers of M
Comparing powers of L

23. Problem 7: contd….
Evaluating 2:
Comparing powers of T
Comparing powers of M
Comparing powers of L
Evaluating 3:
Comparing powers of T Comparing powers of M
Comparing powers of L

24. Problem 7: contd….
Evaluating 4:
Comparing powers of T
Comparing powers of M
Comparing powers of L

25. Model Analysis - Similarity and similitude:
• One of the main application of dimensional analysis is in model testing or
model analysis.
• The study of models of actual machines is called Model analysis.
• Model testing - for predicting the performance of the actual machines, a
model of the machine is made and tests are conducted on it to obtain the
desired information.
• Model is a small scale replica of the actual structure or machine (prototype).
To represent the actual machine under test conditions it should be similar to
the actual machine or prototype or should have similitude.
• Similitude is defined as the similarity between the model and its prototype
in every respect, which means that the model and prototype have similar
properties or model and prototype are completely similar.
• Note: Model may also represent large scale replicas of their prototypes, e.g.,
miniature parts of a watch

26. Types of similarities
• Three types of similarities must exist between the model and prototype.
They are
(a) Geometric similarity,
(b) Kinematic similarity
(c) Dynamic similarity.
• The model and its prototype are said to be completely similar, when all the
above three similarities exist between them

27. (a) Geometric similarity:
• It is said to exist between the model and the prototype if
the ratio of all corresponding linear dimensions in the
model and prototype are equal.
• If Lm, bm, hm, Dm, Am and Vm are length, breadth, height,
diameter, area, and volume of model respectively, and
• Lp, bp, hp, Dp, Ap and Vp are length, breadth, height,
diameter, area and volume of the prototype respectively,
Types of similarities – contd…
Then for geometric similarity,   
p p p
r
m m m
L b D
L
L b D
where Lr is the scale ratio.
Then for area’s ratio,
2

   

p p p
r r r
m m m
A L b
L L L
A L b
Then for volume’s ratio,
3
 
    
 
p p p P
r r r r
m m m m
V L b h
L L L L
V L b h

28. (b) Kinematic similarity:
• If similarity of motion between model and prototype
exists, then kinematic similarity is said to exist between
the model and prototype.
• Kinematic similarity is said to exist, if the ratios of the
velocity and acceleration at the corresponding points in
the model and at corresponding points in prototype are
the same.
• The directions of the velocities accelerations must the
same in prototype and model
Types of similarities – contd…
• If Vp1, Vp2 = velocities of the fluid in the prototype, at points 1 and 2 respectively,
• If am1, am2 = accelerations of the fluid in the prototype, at points 1 & 2 respectively,
• If Vm1, Vm2, am1, am2 = corresponding values of velocities and accelerations at the
corresponding points of fluid in the model,
1 2
1 2

p p
m m
V V
V V
• Then for kinematic similarity, 1 2
1 2

p p
m m
a a
a a
and

29. (c) Dynamic similarity:
• It means the similarity of forces between the model and prototype.
• Thus dynamic similarity is said to exist between the model and prototype if the
ratios of the corresponding forces acting at the corresponding points are equal.
• Also the directions of the corresponding forces at the corresponding points should
be same.
• Mathematically,
Types of similarities – contd…
 
 
 
 
 
 
......
   
g
i v
p p p
r
i v g
m m m
F
F F
F
F F F
where, Fi = inertial force, Fv = viscous force,
Fg = gravitational force and Fr = force ratio

30.  Dimensionless numbers are nothing but the dimensionless groups or Pi terms
formed in given problem.
 It is often possible to provide physical interpretation to these dimensionless
numbers which can be helpful in assessing their influence in a particular
application.
 There are two ways one can obtain dimensionless numbers:
1. Using Buckingham’s Pi theorem
2. Defining them as the ratio of forces
• The dimensionless numbers can be represented in terms of ratio of forces which
are dominant in the problem.
Dimensionless numbers:

31. Types of forces in a moving fluid
1. Viscous Force (FV): It is equal to product of shear stress due to viscosity and
surface area of flow . It comes into picture where viscosity is dominant in a fluid
flow analysis.
2. Gravity force (Fg): It is equal to product of mass and acceleration due to gravity of
the flowing fluid. It is present in case of open surface flows.
3. Pressure force (Fp): It is equal to the product of pressure intensity and cross
sectional area of the flowing fluid. It is present in case of pipe flow.
4. Surface tension force (Fs): It is equal to the product of surface tension and length
of surface of the flowing fluid.
5. Elastic Force (Fe): It is equal to the product of elastic stress and area of the
flowing fluid.
• The net force acting on a fluid is the dynamic force, FD = FV + Fg + Fp + Fs + Fe
• According to D’Alembert’s principle, FD = -Fi  FD + Fi = 0
 Fi + FV + Fg + Fp + Fs + Fe = 0
Dimensionless numbers – contd…
where, Fi = inertia force

32. • The dimensionless numbers are proportional to the ratio of the inertia force (Fi) to
the forces (Fv, Fg, Fp, Fs, Fe) which are dominant in the problem
Dimensionless numbers – contd…
Dimensionless
number
Dominant
force
Ratio of
forces
Application
(1) Reynold’s
number (Re)
Viscous force
(Fv)
Re  Fi /Fv
pipe flow, boundary layer flow, resistance experienced by
submarines airplanes, fully immersed bodies etc.
(2) Froude’s
number (Fr)
Gravity force
(Fg)
Fr  Fi /Fg
Free surface flow, Flow of jet from an orifice or nozzle,
waves formation, fluids of different densities flowing over
one another.
(3) Euler’s
number (Eu)
Pressure force
(Fp)
Eu  Fi /Fp
Capillary rise in narrow passages
Capillary movement of water in soil
Flow over weirs for small heads.
(4) Weber’s
number (Wb)
Surface tension
force (Fs)
Wb  Fi /Fs
Flow over wires with low heads.
Flow of very thin sheet of liquid over a surface.
Capillary flows.
(5) Mach
number (M)
Elastic force
(Fe)
M  Fi /Fe
Aerodynamic testing where velocity exceeds speed of
sound, (airplane flying at supersonic speed), Water hammer
problems.

33. Dimensionless numbers – contd…
(1) Reynold’s number: It is defined as the ratio of inertia force Fi of a flowing fluid and
the viscous force Fv of the fluid. The expression for Reynold’s number is obtained as
follows:
For pipe flow problem, characteristic length L = diameter d

34. Dimensionless numbers – contd…
(2) Froude’s number: it is defined as the square root of the ratio of inertia force Fi of a
flowing fluid to the gravity force Fg. Mathematically we can interpret as follows:
Inertia force

35. Dimensionless numbers – contd…
(3) Euler’s number: it is defined as the square root of inertia force Fi of a flowing fluid
to the pressure force Fp. Mathematically we can express it as follows:

36. Dimensionless numbers – contd…
(4) Weber’s number: it is defined as the square root of the ratio of the inertia force Fi
of a flowing fluid to the surface tension force Fs. Mathematically it is expressed as
follows:

37. Dimensionless numbers – contd…
(5) Mach’s number: It is defined as the square root of ratio of the inertia force Fi of a
flowing fluid to the elastic force Fe. Mathematically it is defined as follows:

38. Model laws OR Similarity laws:
• To satisfy the dynamic similarity between model and prototype, the
dimensionless numbers should be same/equal for the model and prototype.
• But it is difficult to simultaneously satisfy the equality of ALL dimensionless
numbers between the model and prototype.
• Therefore, only the equality of dimensionless number/s between model and
prototype corresponding to the predominant forces is/are considered.
• Similarity law is named, based on which dimensionless number is
considered/predominant:
1. Reynold’s model law  (Re)m = (Re)p  Fv predominant
2. Froude’s model law  (Fr)m = (Fr)p  Fg predominant
3. Euler’s model law  (Eu)m = (Eu)p  Fp predominant
4. Weber’s model law  (Wb)m = (Wb)p  Fs predominant
5. Mach’s model law  (M)m = (M)p  Fe predominant

39. (1) Reynold’s model law: Reynold’s model law is the law in which models are based on
Reynold's number. Which means Reynold’s number for model and prototype must be
the same
Application of Reynold’s model law:
Pipe flow, boundary layer flow, resistance
experienced by submarines airplanes, fully
immersed bodies etc.
Model laws OR Similarity laws – contd…

40. Model laws OR Similarity laws – contd…
(2) Froude’s model law: Froude’s model law is the law in which models are based on
Froude's number. Which means Froude’s number for model and prototype must be
the same.
Froude’s law can be applied in the following cases:
• Free surface flow such as flow over spill ways, weirs, sluices, channels etc.
• Flow of jet from an orifice or nozzle.
• Where waves are likely to be formed on the surface
• Where fluids of different densities flow over one another.

41. Model laws OR Similarity laws – contd…
(3) Euler’s model law: Euler’s model law is the law in which models are based on
Euler's number. Which means Euler’s number for model and prototype must be the
same.
m
 
   

   
   
   p
V V
P P
(Eu)m = (Eu)p
It is applied in the following cases:
• Capillary rise in narrow passages
• Capillary movement of water in soil
• Flow over weirs for small heads.
𝑉
ൗ
𝑃
𝜌
𝑟
= 1

42. Model laws OR Similarity laws – contd…
(4) Weber’s model law: Weber’s model law is the law in which models are based on
Weber's number. Which means Weber’s number for model and prototype must be the
same.

43. Model laws OR Similarity laws – contd…
(5) Mach’s model law: Mach’s model law is the law in which models are based on
Mach’s number. Which means Mach’s number for model and prototype must be the
same.

44. Numerical problems on similitude and model laws:
Problem 8: A pipe of diameter 1.5 m is required to transport an oil of specific gravity
0.9 and viscosity 0.003 poise at the rate of 300 liters/s. Tests were conducted on a 15
cm diameter pipe using water at 20oC. Find the velocity and rate of flow in the
model. Viscosity of water at 20oC is 0.01poise.

45. Problem 8 Contd…

46. Problem 9: The ratio of lengths of a sub marine and its model is 30:1. The speed of
submarine is 10 m/s. the model is to be tested in a wind tunnel. Find the speed of air
in wind tunnel. Also determine the ratio of the drag between the model and
prototype. Take the value of kinematic viscosities for sea water and air as 0.012 and
0.016 stokes respectively. The density of sea water and air is given as 1030 kg/m3 and
1.24 kg/m3 respectively.
(Sub-marine)

47. Problem 9 Contd…
Drag force F = Mass x acceleration
F = density x volume x velocity/time
F =  x L3 x V/(L/V) = L2V2