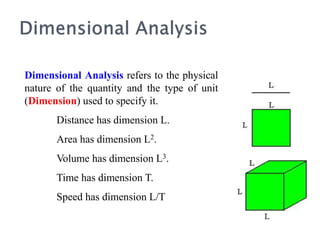
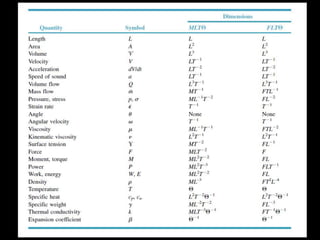
- Dimensional analysis is a technique used to determine the relationship between variables in a physical phenomenon based on their dimensions and units. - It allows reducing the number of variables needed to describe a phenomenon through the use of dimensionless parameters known as π terms. - Lord Rayleigh and Buckingham developed systematic methods for dimensional analysis. Buckingham's π-method involves identifying all variables, their dimensions, and grouping them into as many dimensionless π terms as needed to describe the phenomenon.

3. In 1915, Lord Rayleigh suggested:
 “to think before performing complex and expensive
experiments”.
 Many practical flow problems of different nature can be
solved by using equations and analytical procedures.
However, solutions of some real flow problems depend
heavily on experimental data and the refinements in the
analysis are made, based on the measurements.
 Sometimes, the experimental work in the laboratory is not
only time-consuming, but also expensive. So, the
dimensional analysis is an important tool that helps in
correlating analytical results with experimental data for such
unknown flow problems.
 Also, some dimensionless parameters and scaling laws can be
framed in order to predict the prototype behavior from the
measurements on the model.

4.  Usually we find it impossible to determine all the
essential facts for a given fluid flow by pure theory
alone, so we must often depend on experimental
investigations.
 We can greatly reduce the number of tests needed
using dimensional analysis and laws of similitude
or similarity.
 The similarity law enables us to experiment with a
convenient fluid such as water or air and then
apply these results to a fluid that is less convenient
to work with, such as hydrogen, steam or oil.

5.  The laws of similitude enables us to predict
the performance of prototype (full size
device) from test made with model.
 We need not to use the same fluid for the
model and prototype. Neither must the model
necessarily be smaller than its prototype.
 Example of models: Ships in towing basins,
airplanes in wind tunnel, hydraulic turbines,
spillways of dam, river channels, study of
such phenomenon as the action of waves an
tides on beaches, soil erosion, transport of
sediment.

6.  Model: is the small scale replica of the actual
structure or machine. It is not necessary that
models should be smaller than the prototypes
(although in most of the cases it is), they may be
larger than the prototypes.
 Prototype: The actual structure or machine
 Model analysis: the study of models of actual
machine.

7. • In experimental fluid mechanics we sometimes can not work with real sized objects,
known asprototypes.
• Instead we usescaled down (or up) versions of them, called models.
• Also sometimes in experiments we use fluids that are different than actual working
fluids, e.g. we use regular tap water instead of salty sea water to test the
performance of amarine propeller.
www.reuters.com
www.boeing.com
Wind tunnel tests ofan airliner Racecar being tested in awater tunnel

8. Japan Tsunami 2011
Experimental modelling to study flow behavior.
How flows become floods

9.  Advantages:
 The performance of the machine can be easily
predicted, in advance.
 With the help of dimensional analysis, a
relationship between the variables influencing a
flow problem in terms of dimensional parameters
is obtained.
 This relationship helps in conducting tests on the
model.
 The merits of alternative designs can be predicted
with the help of model testing. The most
economical and safe design may be, finally,
adopted.

10.  It is a pure mathematical technique to establish a
relationship between physical quantities involved in
a fluid phenomenon by considering their
dimensions.
 Dimensional Analysis: The systematic procedure of
identifying the variables in a physical phenomena
and correlating them to form a set of
dimensionless group is known as dimensional
analysis.

11. Dimensional Analysis refers to the physical
nature of the quantity and the type of unit
(Dimension) used to specify it.
Distance has dimension L.
Area has dimension L2.
Volume has dimension L3.
Time has dimension T.
Speed has dimension L/T

12.  Development of an equation for fluid
phenomenon
 Conversion of one system of units to another
 Reducing the number of variables required in
an experimental program
 Develop principles of hydraulic similitude for
model study

13.  MLT system
 FLT system
These two systems are inter-related
F = ma 2nd Law of motion
F = MLT-2 (mass (Kg) x acceleration (meter/second2)
M = FL-1T2

15.  Fundamental Quantities:
◦ Length (L) , mass (M) , time (T).
◦ Some time temperature (θ) is also used as a
fundamental quantity.
 Secondary quantities: are those which
possess more than one fundamental
dimension.
◦ Example: Velocity (L/T)
◦ Acceleration (L/T2)
◦ Density (M/L3)

16.  find yourself a number of physical parameters
generally involved in Physics and specially in
Fluid Mechanics, write and submit the
dimensions with their units and memorize
them.

17.  If the fundamental dimensions and their
respective powers are identical on either sides of
the sign of equality then equation is said to be
dimensionally homogeneous.
Q = A.V continuity equation (homogeneous) i.e.
L3T-1 = L3T-1
Whereas in case of beam shear stress
V = 2√fc’ bw d
FL-2 = [FL-2]1/2L.L
FL-2 = [F1/2L] is dimensionally non homogeneous

19.  If the number of variables involved in a
physical phenomenon are known, then the
relation among the variables can be
determined by the following two methods.
◦ Rayleigh’s Method
◦ Buckingham’s π-method

20. Functional relationship between variables is
expressed in the form of an exponential
relation which must be dimensionally
homogeneous
if “y” is a function of independent variables
x1,x2,x3,…..xn, then
)
,.......
,
,
( 3
2
1 n
x
x
x
x
f
y 

21. In exponential form as
]
)
,.......(
)
(
,
)
(
,
)
[( 3
2
1
z
n
c
b
a
x
x
x
x
y 


22.  Write fundamental relationship of the given data
 Write the same equation in exponential form
 Select suitable system of fundamental dimensions
 Substitute dimensions of the physical quantities
 Apply dimensional homogeneity
 Equate the powers and compute the values of the
exponents
 Substitute the values of exponents
 Simplify the expression
 Ideal up to three independent variables, can be
used for four.

23.  For further understanding, lets explore the
equation for the velocity (V) of a pressure
wave through a fluid.
 First it should be visualised what physical
factors actually influence the velocity
 Compressibility density ρ and kinematic
viscosity υ are the physical factors influencing
the motion.

E

24.  The dimensions of these quantities will be



































T
L
L
M
LT
M
L
F
E
T
L
V
2
3
2
2
,
,




25. C is the dimensionless constant. Substituting
the dimensions
d
b
a
CE
V 



d
b
a
T
L
L
M
LT
M
T
L





















2
3
2

26.  For dimensional homogeneity, the exponents
of each dimension must be identical on both
sides.
 For M
 For L
 For T
b
a 

0
d
b
a 2
3
1 



d
a 


 2
1

27.  Solving the above equations, we get
 So finally,
0
2
/
1
2
/
1




d
b
a


E
C
V 

28.  Use the definition to determine the
dimensions of viscosity.

 Since the expression is dimensionless,
use the same expression to derive dimensions
of µ.

29.  Dimensional analysis was developed in such
way by Lord Rayleigh.
 Very serviceable method but has been
superseded.

30.  Developed by E. Buckingham (1915)-a more generalized
method of dimensional analysis.
 “If ‘n’ is the total number of variables in a dimensionally
homogenous equation containing ‘m’ fundamental
dimensions, then they may be grouped into (n-m) π
terms.
if y=f(x1, x2, ……xn)
then the functional relationship will be written as
 Suitable where
 Not applicable if (n-m) = 0
0
)
.......
,
( 2
1 
m
n




4

n

31.  List all physical variables and note ‘n’ and ‘m’.
n = total no. of variables
m = eq. containing fundamental dimensions
 Compute number of π-terms
 Write the eq. in functional form
 Write eq. in general form
 Select repeating variables. Must have all of the ‘m’
fundamental dimensions and should not form a π among
themselves
 Solve each π-term for the unknown exponents by
dimensional homogeneity.
0
.]
,.........
,
,
[ 3
2
1 





32.  Consider the factors affecting the drag force
on a sphere.
 These include size of the sphere D, velocity of
the sphere V, density ρ and viscosity μ. So
 Here we see that n=5
0
)
,
,
,
,
( 


V
D
F
f D

33.  Choose a Dimensionless system (MLT or FLT)
and determine the number of fundamental
dimensions involved in the system (m).
 We will choose MLT system so the
corresponding dimension will be
 We can see that here m=3
LT
M
L
M
T
L
L
T
ML
,
,
,
, 3
2

34.  Determine the number of π-terms needed. In
this case they will be n-m=5-3=2.
 Select the primary or repeating variables such
that they must contain all of the m
fundamental dimensions and must not form a
π (dimensionless group) among themselves.
Generally it helps to choose primary variables
that relate to mass, geometry, and kinematics
(flow without forces or energy).
 Choose ρ, D and V as the repeating variables.
The π-terms will then be

35.  Using the principle of dimensional
homogeneity, we can solve for the exponents
on each side of the equation.
 Since π-terms are dimensionless, they can be
replaced by M0L0T0.
D
c
b
a
c
b
a
F
V
D
V
D
2
2
2
1
1
1
2
1








36.  So our expressions will look like
1
0
:
1
3
0
:
1
0
:
1
1
1
1
1
3
0
0
0
1
1
1





























c
T
c
b
a
L
a
M
LT
M
T
L
L
L
M
T
L
M
c
b
a

37.  Solving,
 As
1
1
1
1
1
1
1
1 1
;
1
;
1




























DV
DV
V
D
thus
c
b
a

 /
Re DV


38. 2
2
2
1
1
V
D
F
and
R
D




 
 
0
,
0
,
2
2
1
2
1













V
D
F
R D




39.  This shows that the drag force depends upon the
Reynold’s number which is the ratio of inertial
forces to viscous forces.
 Dimensional analysis only provides a partial
solution to the fluid problems as it depends
entirely on the ability of the individual to perceive
the factors influencing a fluid phenomenon.
 So if an important variable is omitted, then the
results could be entirely different.

40.  The ship is subjected to drag force FD on its hull, created by
water passing over and around its surface. It is anticipated
that this force is a function of the density р, viscosity μ, of
the water, and since waves are produced, their weight,
defined by gravity g, is important. Also the ‘characteristics’
length of the ship, L and the velocity of the flow, influences
the magnitude of the drag. Show how the force depends on
all these variables.

41.  In a laboratory experiment a tank is drained through an orifice from initial
liquid level ℎ0. The time, 𝜏, to drain the tank depends on tank diameter, 𝐷,
orifice diameter, 𝑑, gravitational acceleration, 𝑔, liquid properties, 𝜌 and
𝜇. Determine the Pi groups.
 The diameter, 𝑑, of the dots made by an ink jet printer depends on the ink
properties, 𝜌 and 𝜇, surface tension, 𝜎, nozzle diameter, 𝐷, the distance, 𝐿
, of the nozzle from the paper and the ink jet velocity, 𝑉. Determine the Pi
groups.
 Consider the flow of an incompressible fluid through a long, smooth-
walled horizontal, circular pipe. We are interested in analyzing the
pressure drop, ∆𝑝, over a pipe length of 𝐿. Other variables of the problem
are pipe diameter (𝐷), average velocity (𝑉) and fluid properties (𝜌 and 𝜇).
Determine the Pi groups by a) selecting 𝜌 as a repeating parameter, b)
selecting 𝜇 asarepeating parameter.

42.  During floods 2010,many river embankments were
failed which caused enormous scouring (Length =
Sl and Depth = Sd). For performing experiments in
laboratory, different parameters were identified
which are highlighted in below figure. Determine
different Pi-groups.
Land side
Riverside
hbank
dbank
hw
Sd
Sl
Y
3
1
Z
Wooden bar
Levee

43.  Solve all the related numericals i.e. examples
as well as problems in the text book of Fluid
Mechanics (Joseph B Franzini & E. Finnemore,
10th Edition) related to dimensional analysis.