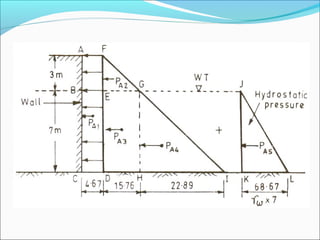
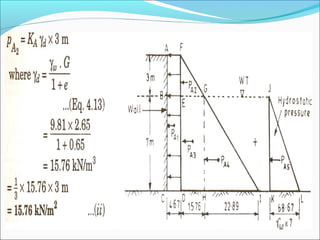
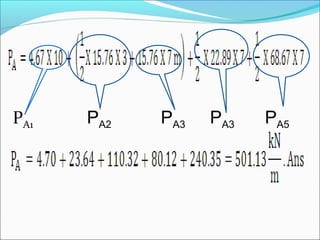
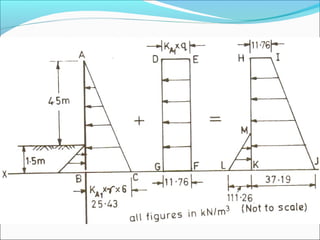
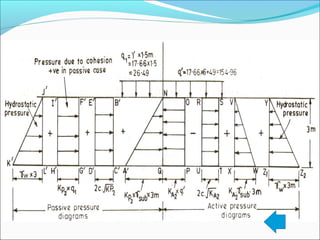
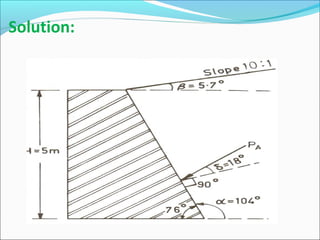
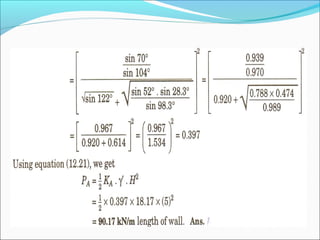
The document contains 10 examples involving calculation of earth pressures on retaining structures using Rankine's and Coulomb's theories. Example 1 calculates active earth pressure on a retaining wall with and without groundwater. Example 2 determines thrust on a wall with the water table rising. Example 3 finds active pressure, point of zero pressure and center of pressure for a cohesive soil. The remaining examples involve calculating earth pressures considering various soil properties and conditions.

2. (a) Compute the active earth
pressure at a depth of 4.5 m in a sand
whose angle of friction is 370
, and
density of 1.56 gm / cc in dry state.
(b) Compute the active earth
pressure also if the water-table is
located at a depth of 1.5 m below the
ground surface. Assume submerged
density of soil as 0.985 gm / cc.
Example-1

3. Solution:
Case (a) the active pressure
distribution in this case is triangular,
with base equal to KA . Y` . H, where H =
4.5 m,
Active pressure at base
PA = KAY` . H = 0.249 X15.30X 4.5 kN/m2
=
17.14 kN/m2
. Ans.

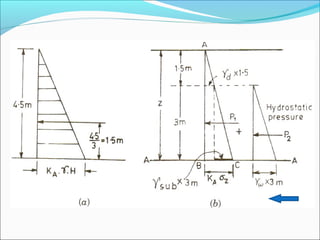
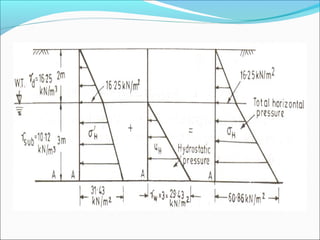
5. Case (b) the pressure distribution in
this case is shown in Fig.
The total active pressure at the base is
given by
PA = [KA . σZ] + [Yw . 3 m]
where σZ = (Ydry X 1.5m + Ysub X 3 m)
PA =0.249 [15.30 x1.5 + 9.66 x 3] + [9.81 x 3]
= 42.36 kN/m2
. Ans.
3
3
/66.9
/81.9
/0.1
/985.0
.
mkN
mkN
ccgm
ccgm
w
w
sub
sub
=
×== γ
ρ
ρ
γ

6.  a. Calculate the total active thrust
on a vertical wall 5 m high, retaining a
sand of density 1.7 gm/cc for which φ =
350
, the surface of the sand is horizontal
and the water–table is below the
bottom of the wall.
 b. Determine the thrust on the
wall if the water-table rises to a level
2m below the surface of the sand. The
saturated density of the sand is 2
Example-2

7. Solution:
(a) The base pressure ordinate in ∆ ABC
= KA . γ` . H
Density of sand = ρ = 1.7 gm/cc
Unit wt. of sand (γ)
Continue

9. Continue

11. A wall with a smooth vertical back,
10 m high, supports a purely cohesive
soil with c = 9.81 kN/m2
and γ = 17.66
kN/m3
. Determine (a) total Rankine’s
active pressure against the wall, (b)
position of zero pressure, (c) distance
of the centre of pressure above the
base.
Example-3

12. Solution:
When soil is purely cohesive, then
φ = 0.
c = 9.81 kN/m2
The base pressure at depth H is given by
the equation
where σz= γ . H = 17.66 X 10 = 176.6 kN/m2
pA = 17.66 X 1 – 2 X 9.81 X √1 = 156.98 kN/m2
BC in Fig.= 156.98 kN/m2
. Continue

13. Before we can determine the total
active thrust, i.e. area of ∆ABC, we have
to determine the point A, i.e. the depth
at which the pressure is zero. This depth
z0 is obtained, using
Continue
AAo KcKz 2.. =γ

14. Hence the pressure is zero at a depth of
1.11 m from the top surface. Ans
m
K
c
z
A
o 11.1
166.17
81.922
=
×
×
==
γ

15. The total thrust can now be worked out as

16. (c) Neglecting the upper tension (as it
does not play any part due to
development of cracks in the earth), the
centre of the active thrust will be the
c.g. of ∆ABC, and is thus located at a
Hence, the centre of pressure acts at
2.96 m above the base. Ans

17. A counterfort wall of 10m height
retains non-cohesive back fill. The void
ratio and angle of internal friction of the
back fill respectively are 0.70 and 300
, in
the loose state, and they are 0.40 and 400
in the dense state. Calculate and compare
active and passive earth pressure in both
the states. Take specific gravity of soil
grains as 2.7. Give your comments on the
result.
Example-4

18. Case. 1. Active pressure Case
Continue

19. Assuming w to be the same in
both cases, or assuming the soil to be
dry in both cases with w = 0, we have
Continue

21. Case. II. Passive pressure Case

22. A smooth vertical wall 4m high is
pushed against a mass of soil having a
horizontal surface and a shearing
resistance given by Coulomb’s equation
in which c = 20 kN/m2
and φ = 300
. The
unit weight of the soil is 20 kN/m3
. Its
surface carries a uniform load of 20
kN/m2
.What is the total passive
Rankine pressure? What is the distance
from the base of the wall to the centre
of pressure?
Example-5

23. Solution:
Following the pressure distribution
diagrams, we can draw the passive
pressure diagram for the instant case,
as shown in Fig.
Continue

24. Continue

26. For an earth retaining structure
shown n Fig. construct earth pressure
diagram for active state and find the
total thrust per unit length of the
wall.
Example-6

27. Solution:
Active pressure caused by surcharge (q) of 14 kN/m2
is
uniform throughout the height, and it equals PA1
=KA .q
= 1/3 x 14 = 4.67 kN/m2
. Its distribution is shown by
rectangle ABCDEF in Fig.
We will first calculate active earth pressure
intensity
3
1
30sin1
30sin1
sin1
sin1
=
+
−
=
+
−
= o
o
ak
φ
φ

30. The pressure diagram will be ΔFEG upto depth B, and
a rectangle EDHG upto bottom with PA3 =PA2 =15.76
kN/m2
.
The active pressure intensity at C due to submerged
soil of 7 m depth consists of pressure due to
submerged soil(pA4 ) and hydrostatic pressure (pA5)
and is given as:
 PA4 = KA .γsub x 7 m
 PA5 = γw . 7 m
Where
( ) ( )
2
5
2
4
3
/67.68781.9
/89.22781.9
3
1
/81.9
65.1
165.281.9
1
1
mkNP
mkNP
mkN
e
G
A
A
w
sub
=×=
=××=
=
−
=
+
−
=
γ
γ

31. The pressure distribution due to
submerged soil will be ∆GHI with
base 22.89 kN/m2
plus ∆JKL due to
water with base width = 68.67 m. The
total active earth pressure diagram is
shown in Fig.
The area of this pressure diagram
will indicate the total active thrust,
and is computed as:
Continue

32. PA1 PA2 PA3 PA3 PA5

33. The soil conditions adjacent to a sheet pile
are shown in Fig., a surcharge pressure
of 49 kN/m2
being carried on the surface
behind the wall. Soil 1 is a sand above the
water-table having effective values of
cohesion and internal friction of 0 and 380
,
and density = 1.8 gm/cc. Soil 2 is a
saturated clay having effective values of
cohesion and angle of friction as 9.8
kN/m2
and 280
respectively, with γsat = 19.6
Example-7
Continue

34. Plot the distributions of the active
pressure behind the wall and the
passive pressure in front of the wall.

35. Solution: For soil 1
For soil 2

36. We will first calculate the pressures at
the junction of the two soils, i.e.
section X-X, say.
Active pressure consists of two
diagrams,as shown in Fig.

38. The ordinates are calculated.

39. The total pressure distribution will
be trapezoidal with top ordinate
equal to 11.76 kN/m2
and bottom
37.19 kN/m2
, as shown by final Fig.
HIJK.
The passive pressure at the base, i.e.
KL = KP1 X γ X 1.5 = 4.2 X 17.66 X 1.5 =
111.26 kN/m2
Continue

40. Now to calculate the pressure
further below i.e. in soil 2, the weight
of the top layer will be considered as
a surcharge on the second soil layer
The weight of the first soil at X-X
= 17.66 kN/m3
X6m = 105.96 kN/m2
Continue

41. The already surcharge coming =49
kN/m2
Hence, the total surcharge to be
considered for soil 2 (q′)
= 105.96 + 49 = 154.96 kN/m2

43. The pressure distribution in soil 2.is
shown in Fig. it consists of four
components,
i.Due to surcharge
ii.Due to submerged weight,
iii.Due to cohesion of soil (-ve), and
iv.Due to hydrostatic pressure

44. The total active pressure ordinate at
the top

45. Passive pressure for soil 2
It consists of three components, i.e
1.Due to surcharge (q1) caused by the
weight of 1.5m depth of the top soil,
2.Due to cohesion component of the 3m
deep soil,
3.Due to submerged weight of 3 m deep
soil,
4.Due to hydrostatic pressure in 3 m
Continue

46. Continue
The total top passive pressure
ordinate(Fig.) left side

47. The total overall passive pressure is
also plotted.

48. A cohesionless soil with a void ratio of
e = 0.6 and specific gravity of soil
solids, Gs = 2.65 exists at a site where
the water table is located at a depth of
2 meter below the ground surface.
Assuming a value of coefficient of
earth pressure at rest k0 = 0.5,
calculate the following quantities at a
depth of 5 meters below the ground
Example-8
Continue

49. total stresses, σV and σH, effective
stresses σ′V and σ′H and p0re water
pressure u.
Assume soil to be dry above the water
table and saturated below the water
table, use γw = 9.81 kN/m3
.

50. Solution:

54. The space behind a masonry retaining wall 5 m
high is backfilled with a granular soil having an
angle of internal friction of 340
. The back face of
wall is inclined at an angle of 760
clockwise to
the horizontal, and the backfill is sloping
upward from top of the wall at a slope of 10:1.
Assuming the angle of wall friction as 180
,
calculate the total active earth pressure on the
wall per metre length. The specific gravity of the
fill soil is 2.70, and has got 20% m.c. at 72%
saturation.
Example-9

55. Solution:

59. A wall of 6 m height retains backfill of dry
granular soil that weighs 18.5 kN/m3
, has a level
surface. When there is no surcharge above fill,
the overturning moment caused by the total
active pressure at a point at the base of the wall
is 150 kN/m length of the wall. The
specifications permit certain amount of
uniformly distributed surcharge but state that
surcharge must not increase overturning
moment by more than 75%. What surcharge can
be allowed if the angle of wall friction is 250
?
Example-10

60. Solution
Since wall friction is to be considered,
we can’t use Rankine’s equation, but
will have to use Coulomb’s equations,
given as:
Continue

61. Continue

62. Continue

63. Continue