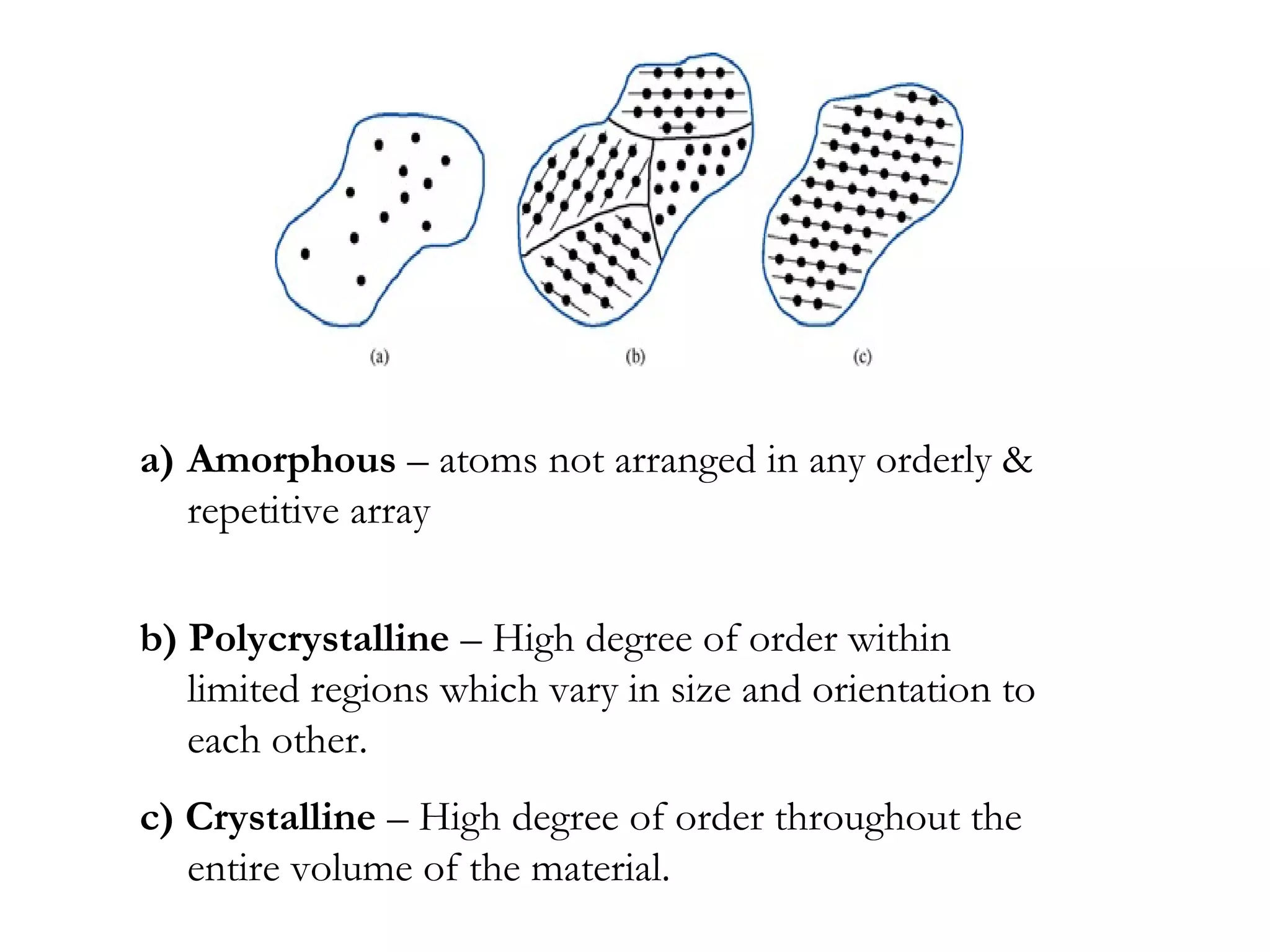
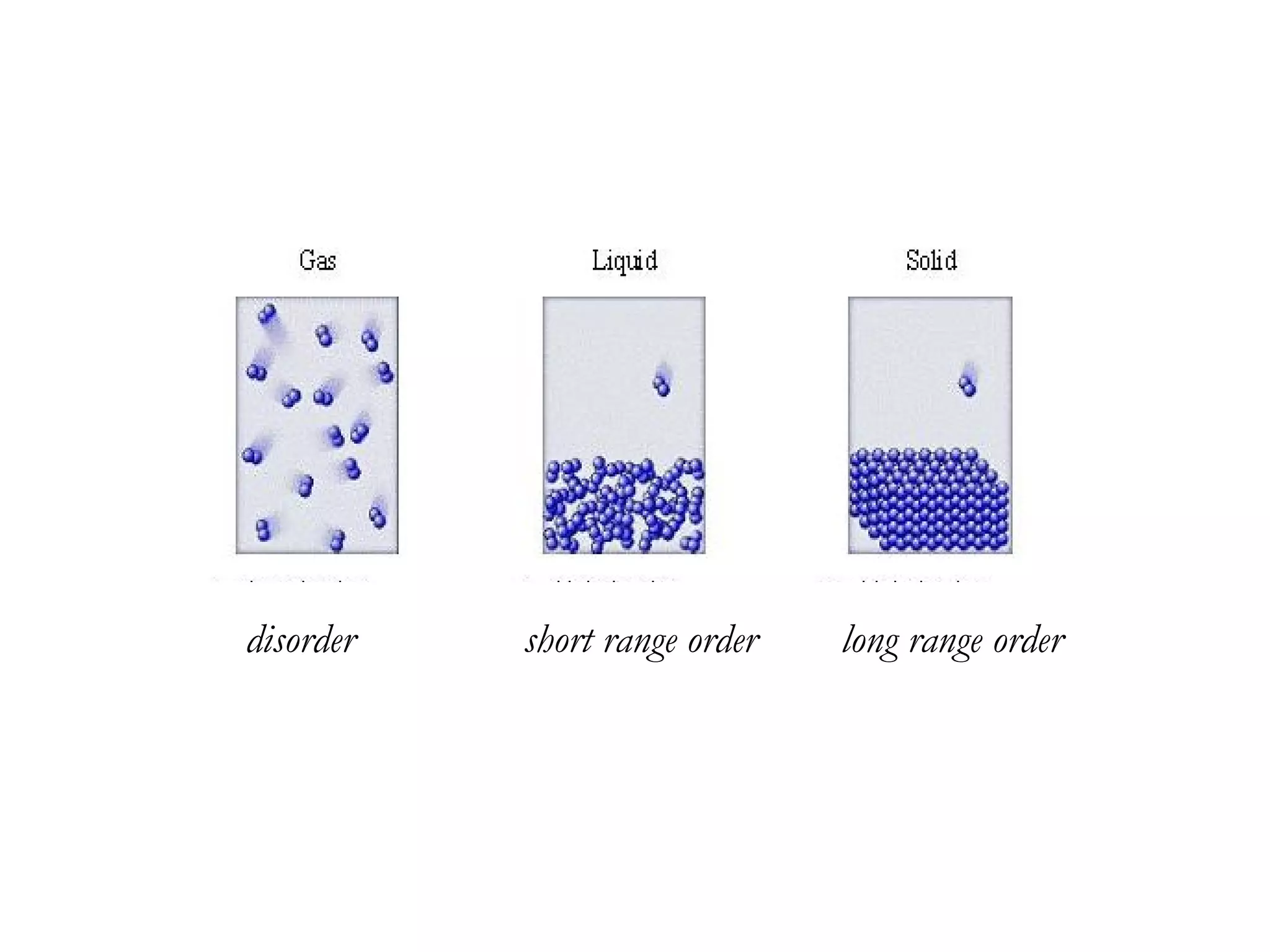
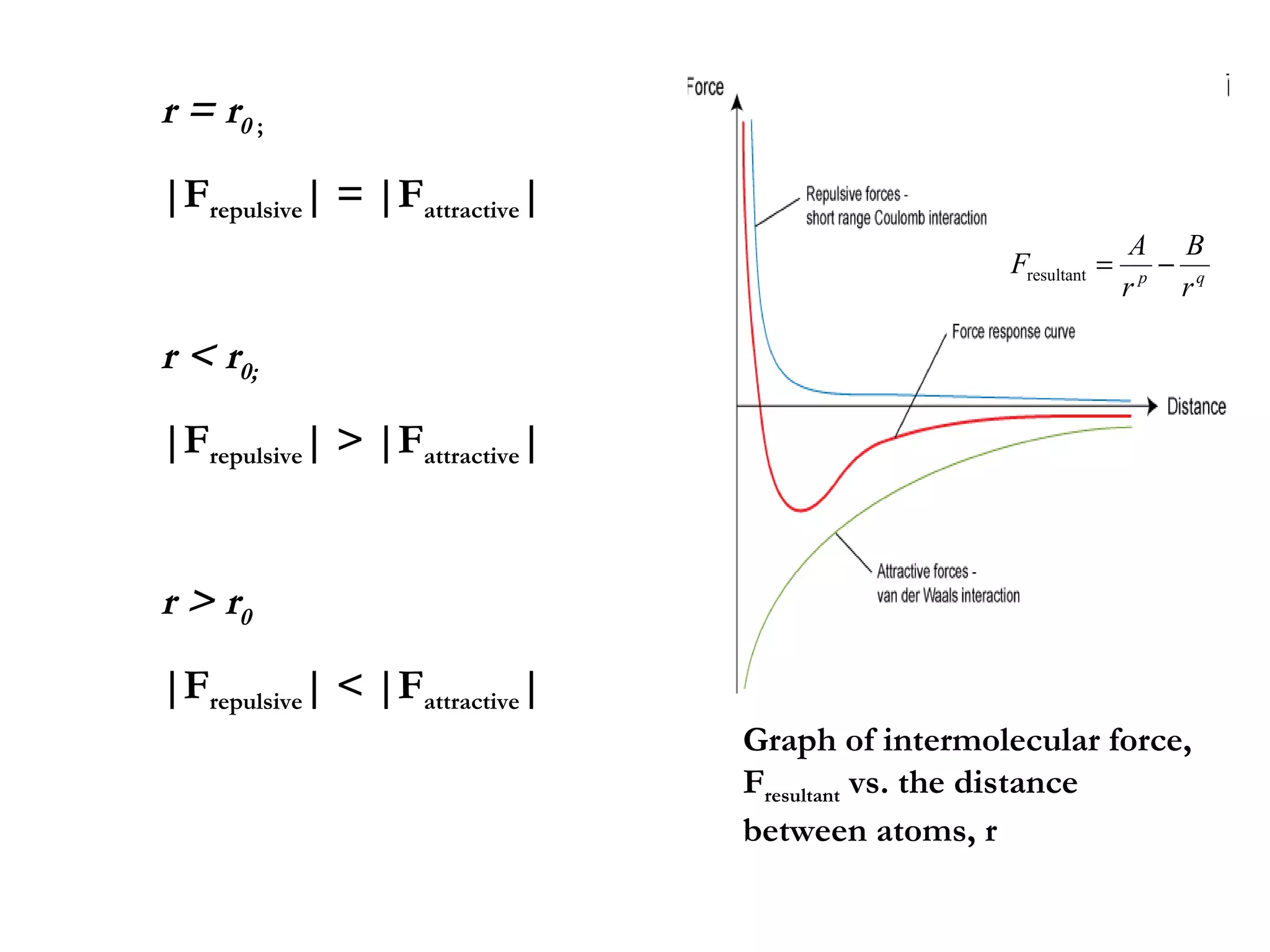
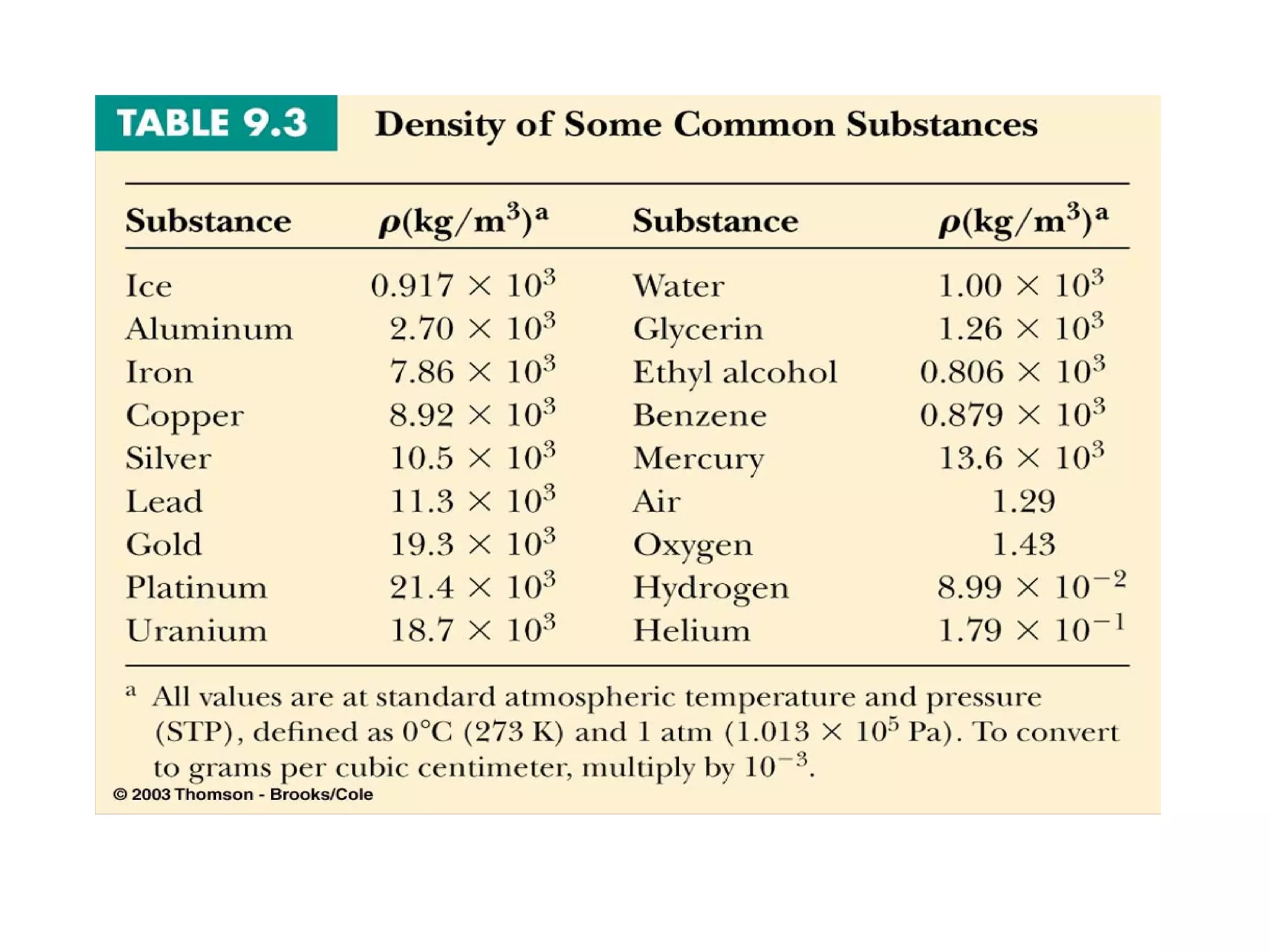
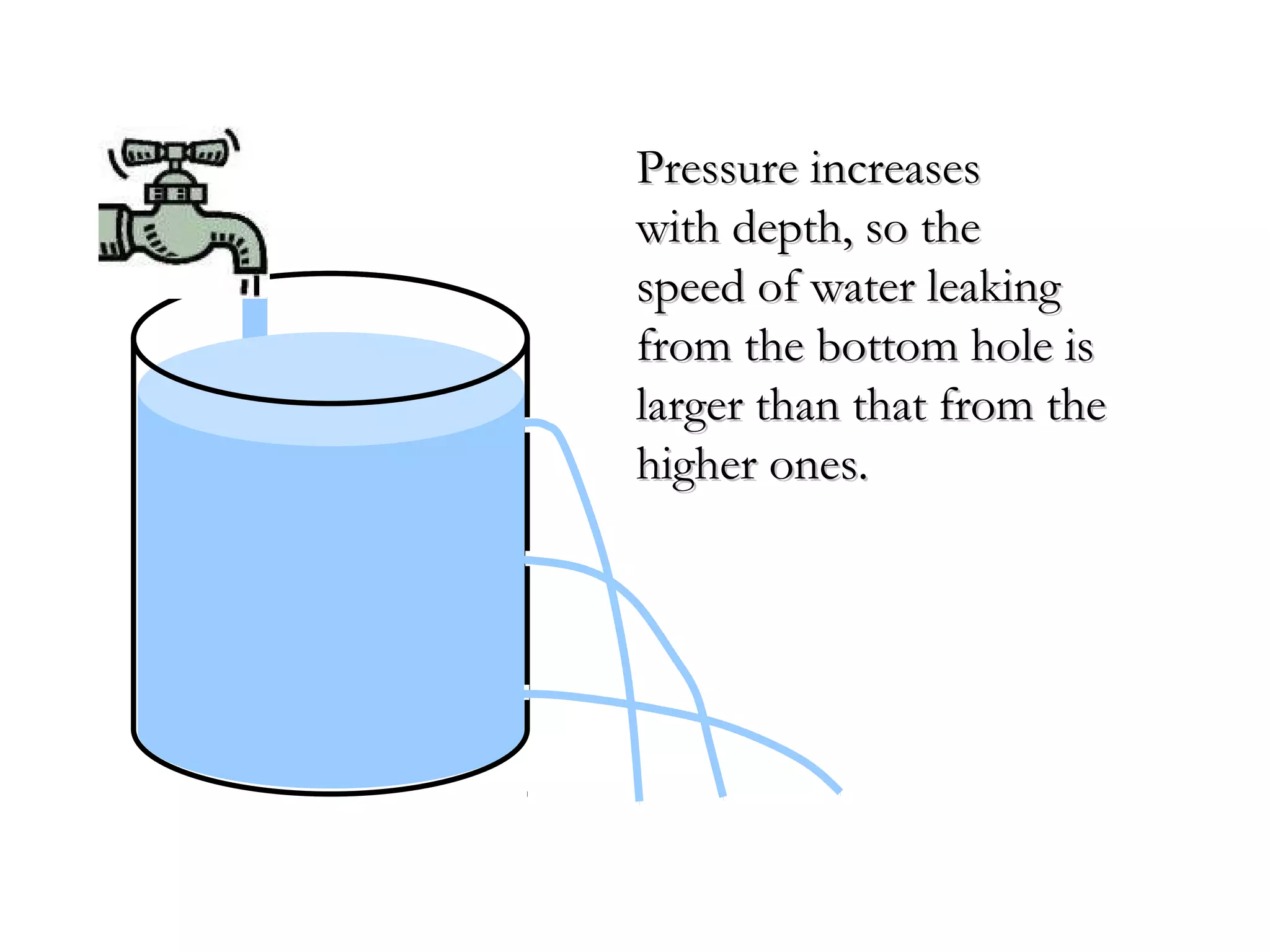
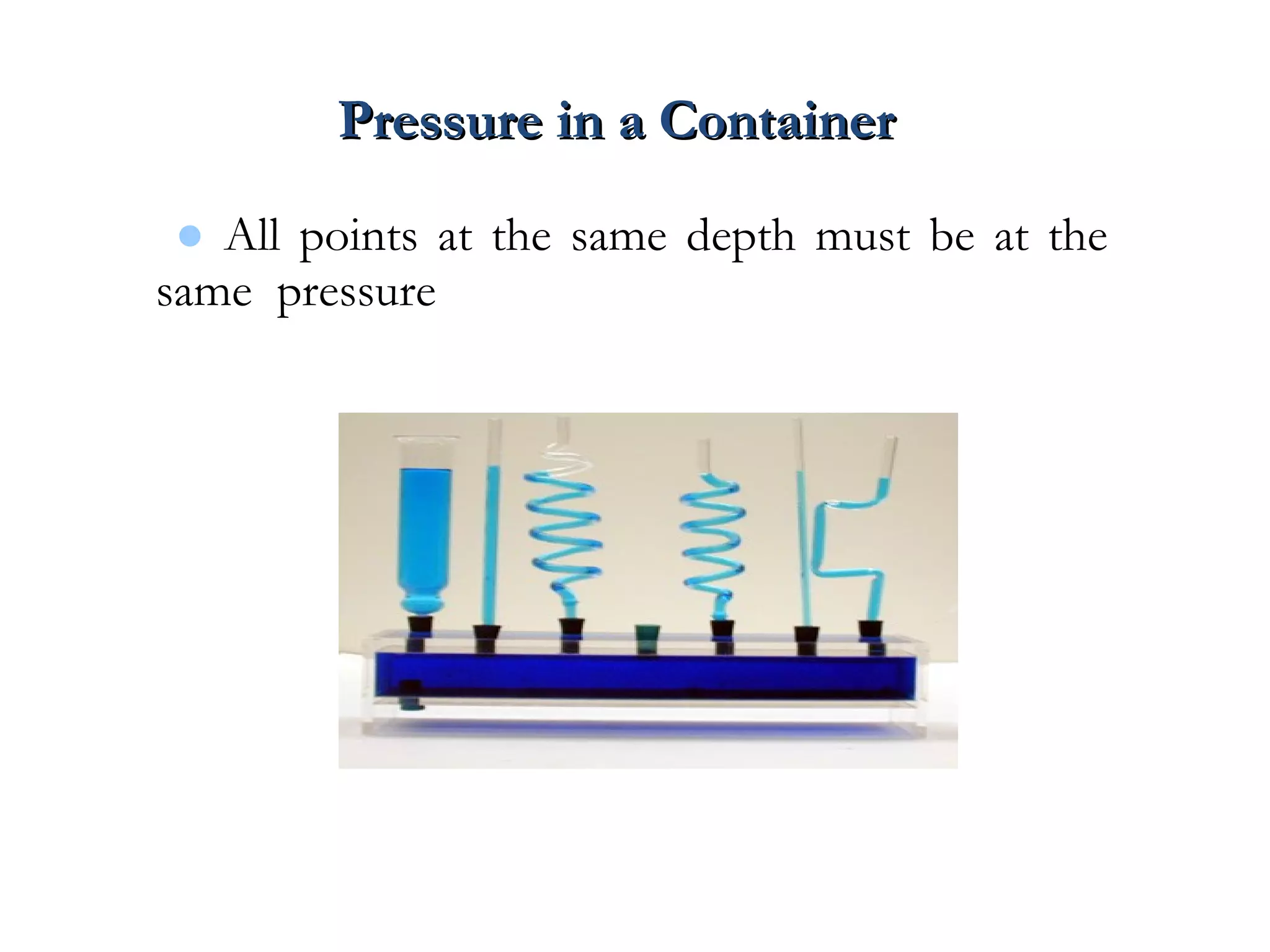
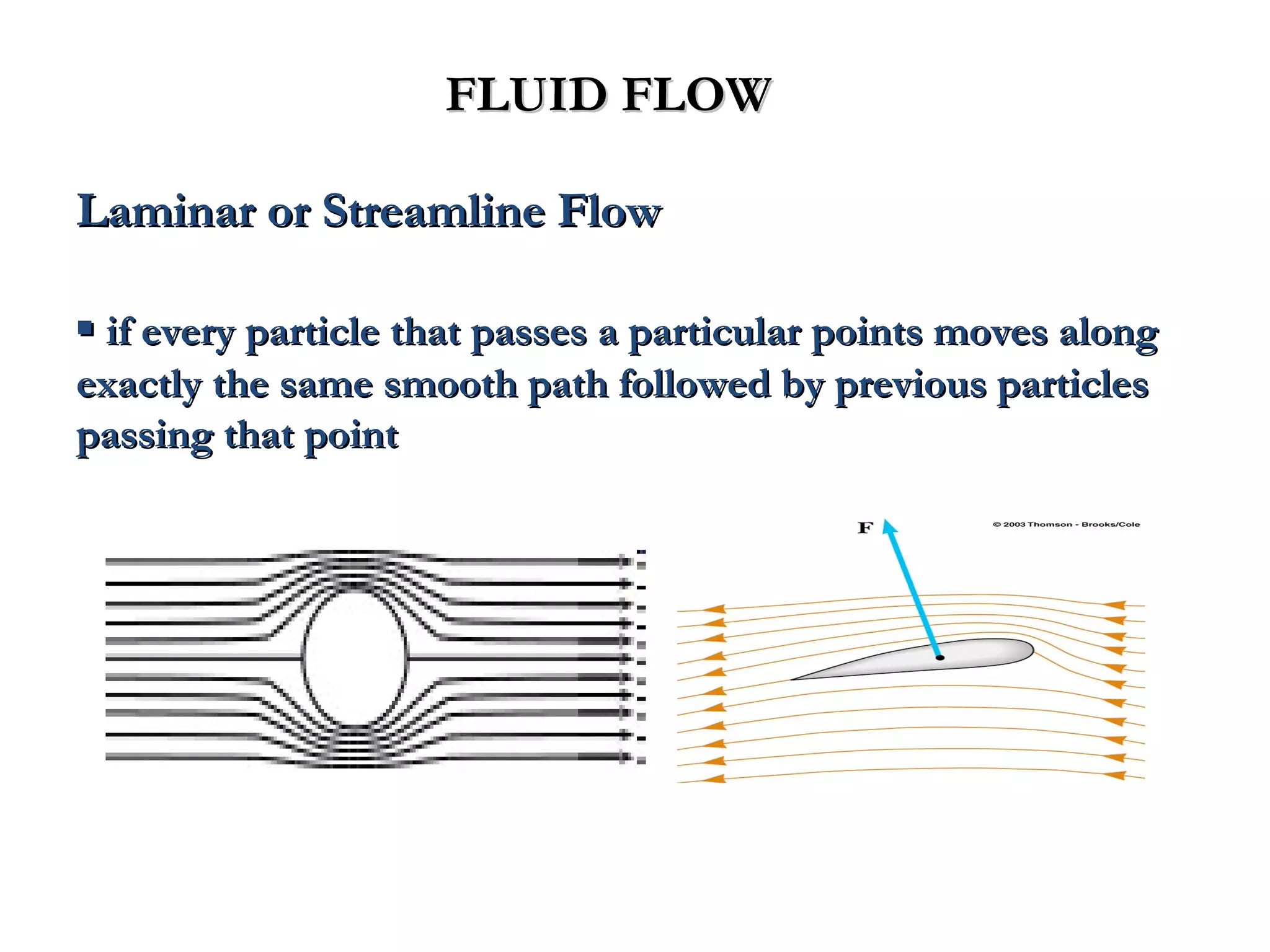
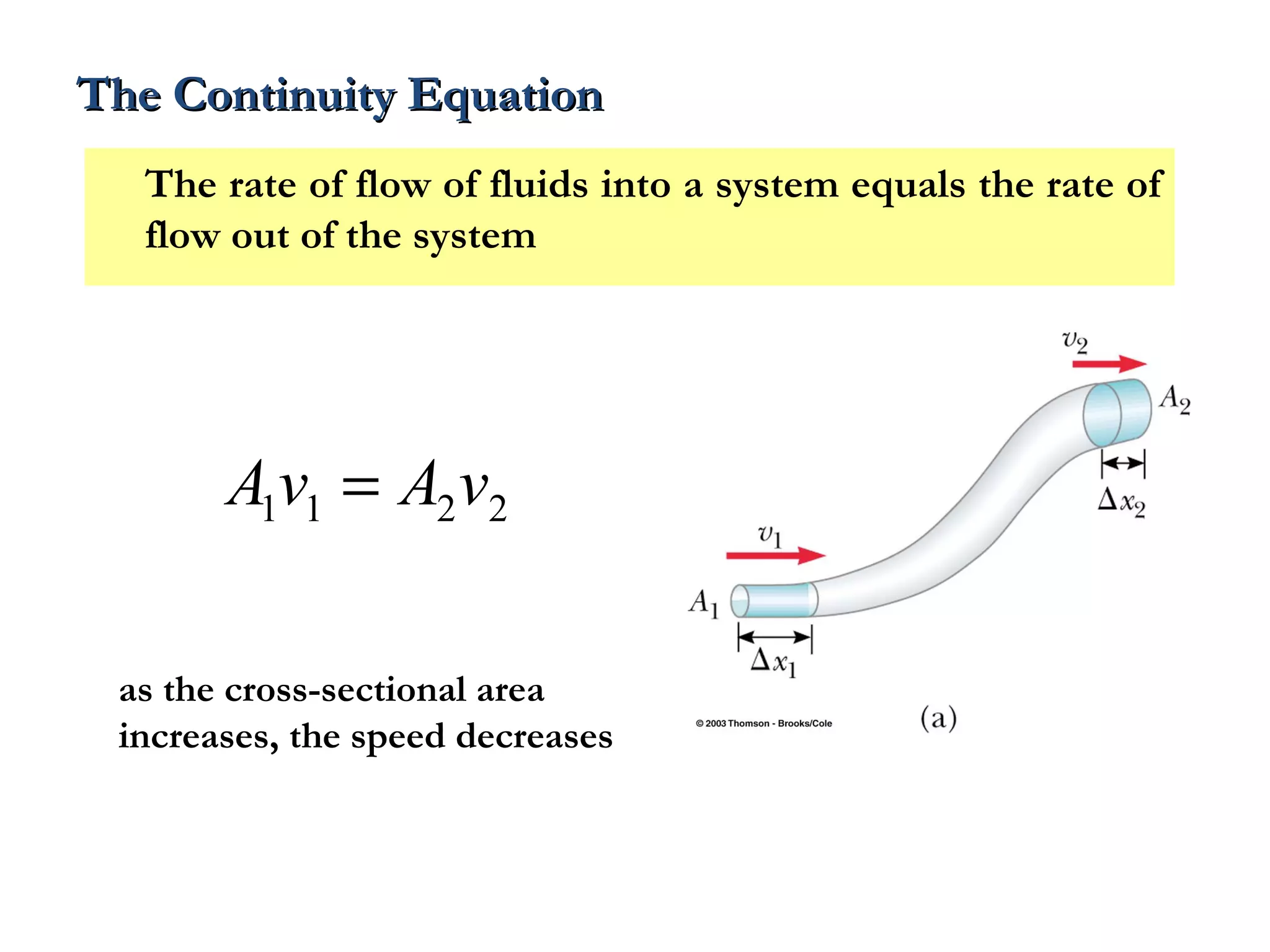
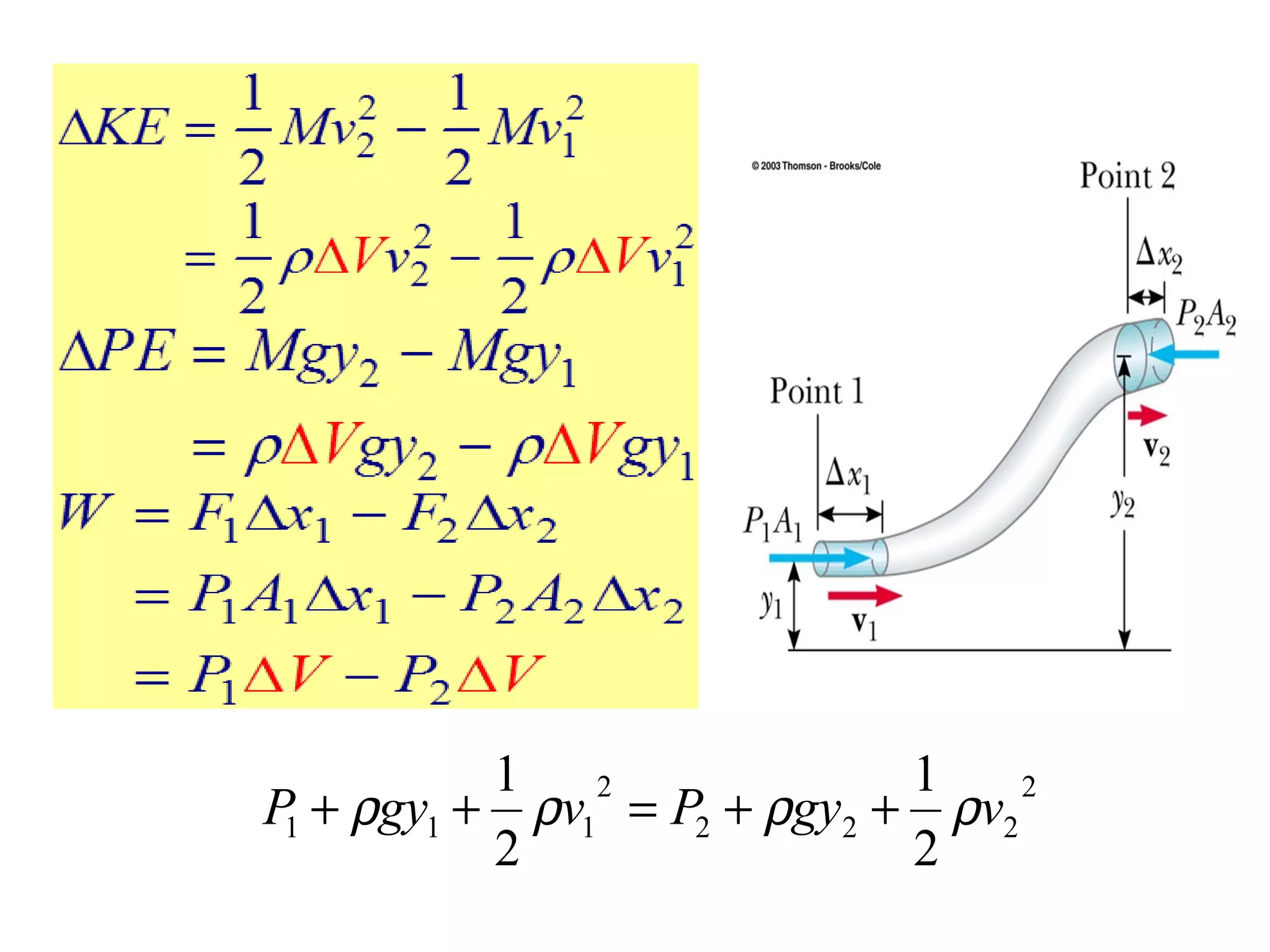
The document discusses the key properties of solids, liquids, and gases. Solids have a definite shape and volume, while liquids have a definite volume but no definite shape and can flow. Gases have no definite shape or volume and expand to fill their container. Solids exhibit long-range order while liquids have weaker binding and shorter-range order. Gases have molecules that are widely separated with disorder prevailing. Intermolecular forces also differ between the three states of matter.

1. SOLID, LIQUID & GAS

2. INTRODUCTION
An understanding of fundamental properties of
different states of mater is important in all science,
engineering, and in a medicine. Force put stresses on
solids, stress can strain, deform, and break those
solids, whether they are steel beams or bones. Fluids
under pressure can perform work, or they carry
nutrient and essentials solutes, like the blood flowing
through our arteries and veins. Flowing gases cause
pressure differences that can lift a massive cargo plane
or the roof off a house in hurricane.

3. Matter?
▪ solid
▪ liquid
▪ gas
What are their characteristics?

4. SOLID
General types of solids :
▪ amorphous
▪ polycrystalline
▪ crystalline
Each type is characteristic by the size of an
order region within the material

5. a) Amorphous – atoms not arranged in any orderly &
repetitive array
b) Polycrystalline – High degree of order within
limited regions which vary in size and orientation to
each other.
c) Crystalline – High degree of order throughout the
entire volume of the material.

6. LIQUID
▪ weaker binding
▪ able to flow
▪ definite volume but no definite shape
▪ density higher than the density of gases

7. GAS
▪ fills container
▪ compressible
▪ flows easily
▪ very low density – each particles are well
separated

8. disorder short range order long range order

9. INTERMOLECULAR FORCES
How the forces between atoms/molecules react?
▪ Frepulsive= Fattractive (at equilibrium r )
▪ atoms repel each other due to repulsive forces
(compressed)
A
Frepulsive = p
r
▪ atoms attract each other corresponding
to attractive force (stretched)
B
Fattractive =− q
r

10. r = r0 ;
|Frepulsive| = |Fattractive|
A B
Fresultant = p
− q
r r
r < r0;
r0
|Frepulsive| > |Fattractive|
r > r0
|Frepulsive| < |Fattractive|
Graph of intermolecular force,
Fresultant vs. the distance
between atoms, r

11. POTENTIAL ENERGY BETWEEN MOLECULES
At equilibrium state distance between two atoms is stable (no
work done) & the potential energy is minimum.
If the force exists, r is change and net of work is done then
change the potential energy.
∆U = −∆W = − F∆r
Minus sign means the force between the atoms is the same
but with the opposite to the applied force

12. DENSITY
an object having uniform composition is defined
as its mass M divided by its volume V
M
ρ=
V
SI unit : kg/m3

14. PRESSURE
defined as the scalar value of the force acting
perpendicular to, and distributed over, a space, divided
by the area of the surface :
F
P=
A
unit : N/m2 / Pascal

15. Variation of pressure with depth
Fluid at the rest (static)
● For this volume not to move (static fluid) we
must have that
FTOP
FBOTTOM = FTOP + mg A
H
FBOTTOM W

16. Variation of pressure with depth
FBOTTOM - FTOP = mg = (density x Vol) x g
FBOTTOM - FTOP = ρ A H g
Since Force = P x A
PBottom A – PTop A = ρ A H g, or
PBottom – PTop = ρ H g
The pressure below is greater
than the pressure above.

17. Pressure in a fluid increases with depth h
Pressure at depth h
Po = Patm
P(h) = Po + ρgh
h
P(h) ρ = density (kg/m3)
= 1000 kg/m3 for water
The pressure at the surface is atmospheric
pressure, 105 N/m2

18. Pressure increases
with depth, so the
speed of water leaking
from the bottom hole is
larger than that from the
higher ones.

19. Pressure in a Container
● All points at the same depth must be at the
same pressure

20. Example:
What pressure (due to the only water) will a swimmer
20 m below the surface of the ocean experience?
Solution:
Given h = 20 m
ρsea water = 1.025 x 103 kg/m3
Thus, P= ρgh =(1.025 x 103 kg/m3)(9.8 m/s2)(20m)
= 2.0 x 105 N

21. Practice 1:
A water bed is 2.00 m on a side and 30.0 cm deep. Find:
a) its weight
b) pressure that the water bed exerts on the floor. Assume
that the entire lower surface of the bed makes contact
with the floor.
Answer :
a) 1.18 x 104 N
b) 2.95 x 103 Pa

22. PASCAL’S PRINCIPLE
a change in pressure applied to an enclosed fluids
is transmitted undiminished to every point of the
fluid and to the walls of the container
F1 A1
=
F2 A2
Hydraulic lifts

23. Practice 2:
In a car lift used in a service station, compressed air exerts
a force on a small piston of circular cross section having a
radius of r1=5.00 cm. This pressure is transmitted by an
incompressible liquid to a second piston of radius r2=15.0
cm.
a) What force must the compressed air exert on the small
piston in order to lift a car weighing 13,300 N? Neglect the
weight piston.
b) What air pressure will produce a force of that magnitude?
Answer :
a) F1 = 1.48 x 103 N b) P = 1.88 x 105 Pa

24. ARCHIMEDES’S PRINCIPLE
any object completely or partially submerged in a fluid
is buoyed up by a force with the magnitude equal to
the weight of the fluid displaced by the object.
FB = F2 − F1
= ρ F gA( h2 − h1 )
= ρ F gA∆h
= ρ F gV
= gmF
The bouyant force equals the weight of the fluid displaced

25. SPECIFIC GRAVITY
The ratio of the mass of a body to the mass of an
identical volume of water is equal to the relative density
ρ m /V m
= =
ρ w mw / V mw
m
= = sp.gr
m − mr
mr = reduced mass
* The sp.gr tell how many times more or less dense a
material is than water

26. SURFACE TENSION
The force per unit length exerted by the liquid surface
on an object, along its boundary of contact with the
object. This force is parallel to the liquid surface and
perpendicular to the boundary line of contact.
γ =F / L

27. The force on the wire
ring is measured just
before the ring breaks
free of the liquid
γ =F / 2L
2L = the surface exerts
force both the side and
outside of the ring

28. FLUID FLOW
Laminar or Streamline Flow
▪ if every particle that passes a particular points moves along
exactly the same smooth path followed by previous particles
passing that point

29. Turbulent Flow
● the flow of a fluid becomes irregular above a certain
velocity or under any conditions that can cause abrupt
change in velocity
● irregular motion is eddy current

30. ▪ The laminar or turbulent behavior of fluids is dependent
by:
a) size of the object moving through the fluid, or the size
of the vessel in which the fluid is moving.
b) velocity of the object, or the fluid relative to the vessel.
c) viscosity of the fluid.
▪ The relationship between these variables is described by
a scaling number, which is dimentionless, called the
Reynolds number, Re.

31. The Continuity Equation
The rate of flow of fluids into a system equals the rate of
flow out of the system
A1v1 = A2 v2
as the cross-sectional area
increases, the speed decreases

32. Bernoulli’s Equation
The sum of the pressure P,the kinetic energy per unit
volume and the potential energy per unit volume has the
same value at all points along the streamlines
1 2
P + ρv1 + ρgy = constant
1
2

33. 1 2 1
P + ρgy1 + ρv1 = P2 + ρgy2 + ρv2
2
1
2 2

34. TORRICELLI’S RESULT
If a tank filled with fluid and open to the atmosphere has
a hole at a depth,h below the surface of the water, then
the speed of the fluid leaving the hole is the same as if
the liquid had freely fallen through a height,h.
v2 = 2 gh

35. VISCOSITY
▪ exists in both liquids and gases
▪ a frictional force between adjacent layers of fluid as
the layers move past one another.
▪ in liquids – due to the cohesive force
▪ in gases – arises from collisions between the molecules
▪ coefficient of viscosity, η (unit Poiseuille, Pl or Pa.s)
▪ the more viscous the fluid, the greater is the required
force.
Av
F =η
l

36. POISEUILLE’S LAW
the rate of the flow depends on the pressure difference,
the dimensions on the tube and the viscosity of the fluid
∆V πR 4 ( P − P2 )
Rate of flow = = 1
∆t 8ηL
L= length ; R=radius; η= coefficient of viscosity,

37. Practice 3:
A patient receives a blood transfusion through a needle
of radius 0.20mm and length 2.0 cm. The density of
blood is 1050 kg/m3.The bottle supplying the blood is
0.50 m above the patient’s arm. What is the rate of flow
through the needle? Given the coefficient of viscosity,η
of blood is 2.7 x 10-5 N.s/m2
Solution :
a) Calculate the pressure difference the level of the blood
and the patient’s arm.
b) Substitute the pressure to the Poiseuille’s equation

38. STOKES LAW
▪ Consider a sphere falling through a viscous fluid. As
the sphere falls so its velocity increases until it reaches
a velocity known as the terminal velocity. At this
velocity the frictional drag due to viscous forces is just
balanced by the gravitational force and the velocity is
constant
Fr = 6πηrv
▪ the terminal velocity is :
mg
vt =
6πηr