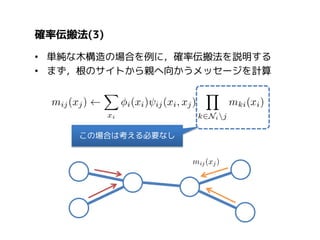
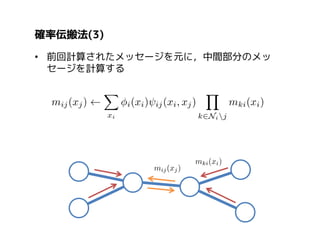
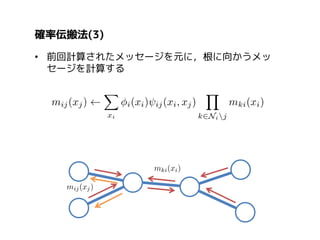
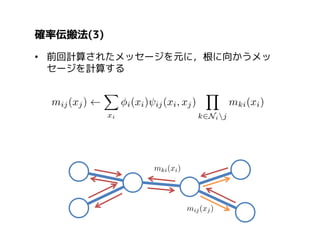
More Related Content
PDF
PDF
SSII2020 [OS2-03] 深層学習における半教師あり学習の最新動向 PDF
PPTX
PDF
Word Tour: One-dimensional Word Embeddings via the Traveling Salesman Problem... PDF
PDF
PDF
What's hot
PDF
PDF
PDF
SSII2021 [OS2-01] 転移学習の基礎:異なるタスクの知識を利用するための機械学習の方法 PPTX
[DL輪読会]ドメイン転移と不変表現に関するサーベイ PPTX
PDF
画像局所特徴量と特定物体認識 - SIFTと最近のアプローチ - PDF
PPTX
PPTX
PDF
【メタサーベイ】基盤モデル / Foundation Models PDF
PDF
PDF
PDF
PDF
自己教師学習(Self-Supervised Learning) PDF
Bayesian Neural Networks : Survey PPTX
Deep Learning による視覚×言語融合の最前線 PDF
Transformerを多層にする際の勾配消失問題と解決法について PPTX
【DL輪読会】Flamingo: a Visual Language Model for Few-Shot Learning 画像×言語の大規模基盤モ... PDF
KDD Cup 2021 時系列異常検知コンペ 参加報告 Viewers also liked
PDF
PDF
PDF
PPTX
医用画像における解剖学的ランドマークの検出、定義および応用 PPTX
PPTX
PDF
PDF
PDF
ベイジアンネットワークモデリング勉強会20140206 PDF
"Estimating Tree-Structured Covariance Matrices via Mixed-Integer Programming" PDF
PDF
PDF
PDF
PPTX
PPTX
PDF
PPTX
PDF
PPTX
Similar to 条件付き確率場の推論と学習
PDF
PPTX
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
基礎からのベイズ統計学 輪読会資料 第4章 メトロポリス・ヘイスティングス法 PDF
PPTX
PPTX
クラシックな機械学習の入門 5. サポートベクターマシン PDF
PDF
渡辺澄夫著「ベイズ統計の理論と方法」5.1 マルコフ連鎖モンテカルロ法 PDF
MLaPP 24章 「マルコフ連鎖モンテカルロ法 (MCMC) による推論」 PPTX
PDF
条件付き確率場の推論と学習
- 1.
- 2.
目次
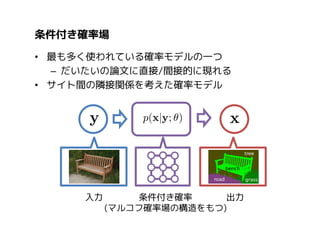
1. コンピュータビジョンと条件付き確率場
2. マルコフ確率場
3.最適化手法
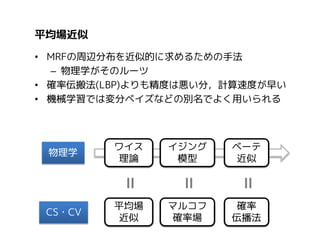
1. 平均場近似
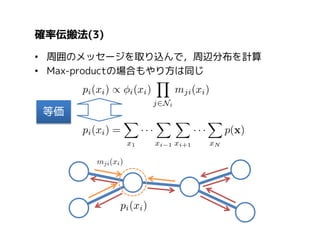
2. 確率伝搬法(max-product, sum-product)
4. 条件付き確率場とその学習
参考文献
Conditional Random Fields(CVPR2011 Tutorial)
http://www.nowozin.net/sebastian/cvpr2011tutorial/slides/talk-crf.pdf
Understanding Belief Propagation and Its Generalizations
http://www.merl.com/papers/docs/TR2001-22.pdf
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
Face Detection, PoseEstimation, and Landmark
Zhu et. al. CVPR2012
Localization in the Wild
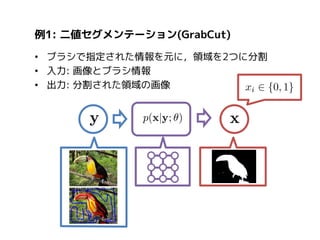
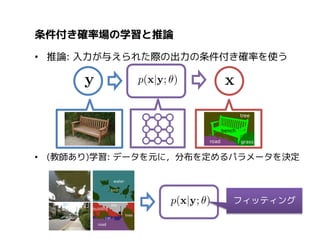
• 写真から複数の顔の位置,
表情を認識
• 顔のパーツ位置同士の関係
を平滑化項として指定
• 木構造のGaussian MRFを
利用,ピーク位置をExact
に求めている
- 9.
Efficient Inference inFully-Connected CRFs
Krahenbuhl et. al. NIPS2010
with Gaussian Edge Potentials
•
•
•
•
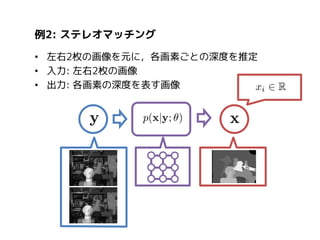
ピクセル毎の一般物体認識
すべての画素がすべての画素に接続(Fully-Connected CRF)
平均場近似を用いて畳み込み積分の形に変形,高速に推論可能
学習は平均場近似を用いた近似学習
- 10.
- 11.
- 12.
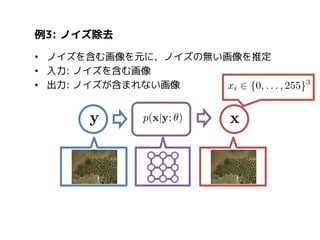
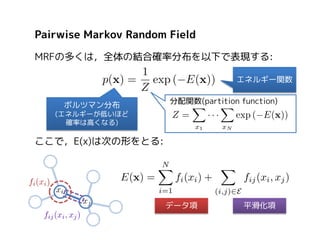
Pairwise Markov RandomField
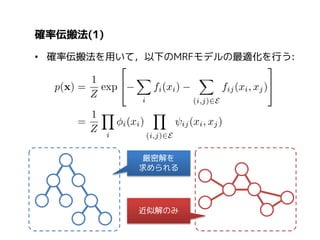
MRFの多くは,全体の結合確率分布を以下で表現する:
エネルギー関数
ボルツマン分布
分配関数(partition function)
(エネルギーが低いほど
確率は高くなる)
ここで,E(x)は次の形をとる:
データ項
平滑化項
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
- 45.
- 46.
- 47.