Download to read offline
画像認識4
- 1.
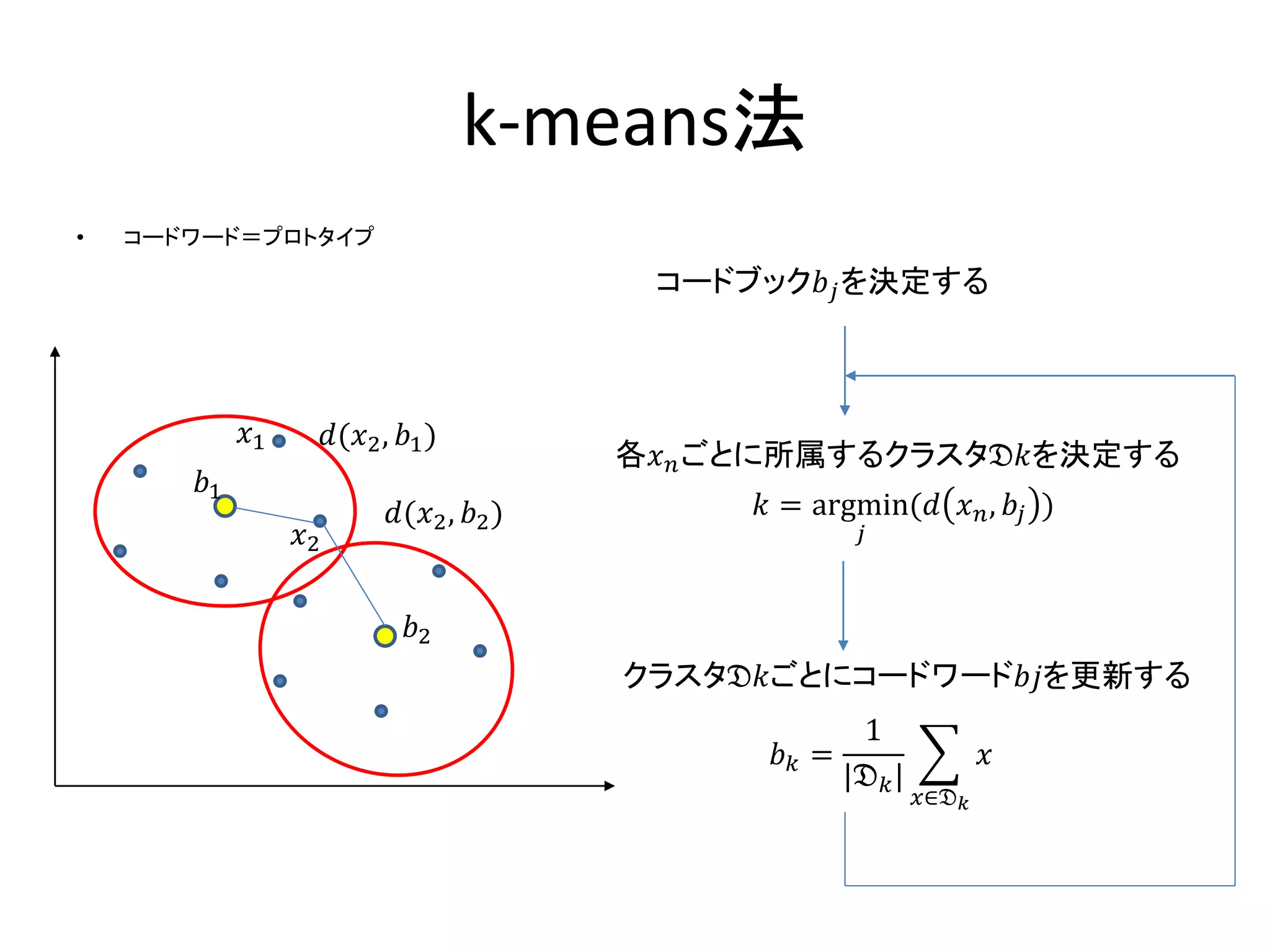
- 2. 4.1.1 コーディング • 原画像から特徴点を抽出 •特徴点から，新たな高次の特徴量へ変換＝ コーディング – 特徴点を別の高次のベクトルに変換 • ある画像領域の複数のコーディングベクトル を１つのベクトルにまとめる＝プーリング – ベクトルの数は減るが，１ベクトルあたりの次元 は同じ
- 3. コーディングの手法 • 確率分布を仮定した推定> 4.2 •代表点 >4.3 • 多様体 >4.4 • カーネルの内積による近似>4.5 • 判別的な学習>4.6
- 4. 4.2.1.1 BoVW • 類似の特徴点をまとめてヒストグラム化する •ある特徴点をどのグループのカウンタをアッ プさせるか – クラスタリング（教師なし学習）問題 • クラスタリングアルゴリズム k-means法 • ２点がどれだけ離れているのかを表す指標 カーネル
- 5. k-means法 • コードワード＝プロトタイプ 𝑏2 𝑏1 𝑥1 𝑥2 𝑑(𝑥2, 𝑏1) 𝑑(𝑥2,𝑏2) 各𝑥 𝑛ごとに所属するクラスタ𝔇𝑘を決定する コードブック𝑏𝑗を決定する 𝑘 = argmin 𝑗 (𝑑 𝑥 𝑛, 𝑏𝑗 ) クラスタ𝔇𝑘ごとにコードワード𝑏𝑗を更新する 𝑏 𝑘 = 1 |𝔇 𝑘| 𝑥∈𝔇 𝑘 𝑥
- 6. カーネル法 𝑦 = 𝔀𝑇 𝒙 𝑟𝑠(𝑦; 𝒙; 𝔀)=(𝑦-𝔀 𝑇 𝒙) 𝟐 𝑅 𝔀 = 𝑗=1 𝑛 𝑟𝑠(𝑦; 𝒙; 𝔀) = 𝑗=1 𝑛 (𝑦−𝔀 𝑇 𝒙) 𝟐 𝑦 = 𝑗=1 𝑛 𝛼𝑗 𝑘(𝒙 𝑗 , 𝒙) 𝑟𝑘(𝑦; 𝒙; 𝜶)=(𝑦- 𝑗=1 𝑛 𝛼𝑗 𝑘(𝒙 𝑗 , 𝒙)) 𝟐 𝑅 𝜶 = 𝒚 − 𝐾𝜶 𝑇 𝒚 − 𝐾𝜶 𝐾 = 𝑘 𝑥(1), 𝑥 1 ⋯ 𝑘 𝑥(1), 𝑥 𝑛 ⋮ ⋱ ⋮ 𝑘 𝑥(𝑛), 𝑥 1 ⋯ 𝑘 𝑥(𝑛), 𝑥 𝑛 最小二乗法 カーネル法 最小二乗法は，サンプルから線形モデル𝔀を生成する．カーネル法は，サンプルから カーネル関数の線形モデル𝜶を生成する．カーネル関数は２点間距離（近さ，類似度） 関数． カイ二乗カーネル／ヒストグラムインターセクションカーネル／ヘリンジャーカーネル等
- 7. 4.2.1.3 カーネルコードブック • ある特徴点はどこかひとつのクラスタに属するの ではなく，いくつかの複数のクラスタに所属させ られる –コードワードからの距離(ガウシアンカーネル）の割合 による 𝑦 = exp(−0.5𝑥2) 𝑏2 𝑏1 𝑥2 𝑑(𝑥2, 𝑏1) 𝑑(𝑥2, 𝑏2) 𝑐 𝑘 𝑥 𝑛 = 𝑒𝑥𝑝 − 𝛾 2 𝑥 𝑛 − 𝑏𝑗 2 𝑗=1 𝐾 𝑒𝑥𝑝 − 𝛾 2 𝑥 𝑛 − 𝑏𝑗 2 𝑥 𝑛は𝑏 𝑘に𝑐 𝑘 𝑥 𝑛 × 100% 寄与している
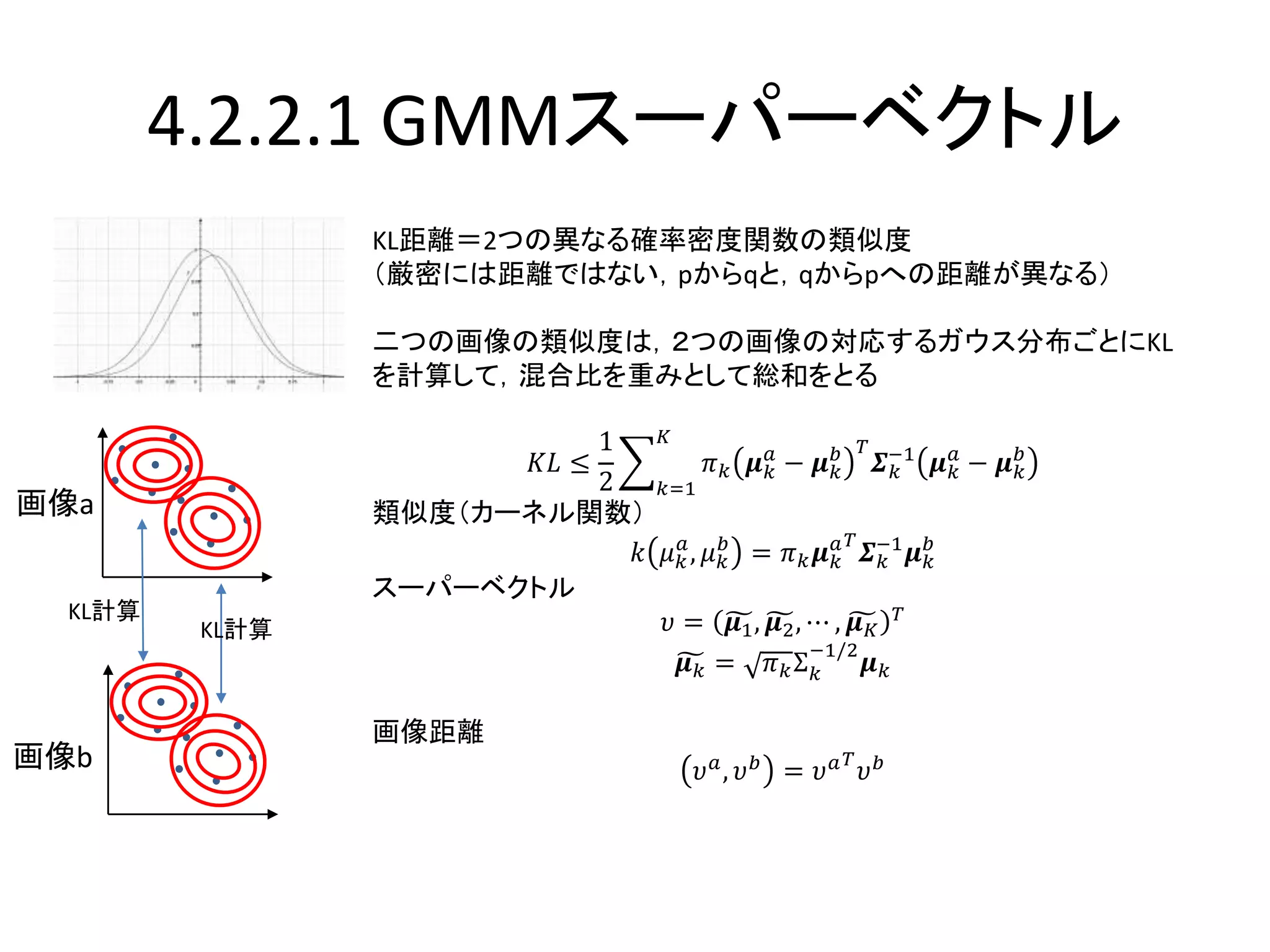
- 8. 4.2.2.1 GMM混合ガウス分布モデル 特徴点をK個のガウス分布からなる確率モデルから生成されたサンプルと仮定して，ガ ウス分布のパラメータを推定する π2=0.3 𝑥 𝑛 0.7𝒩(𝑥|5,1)+ 0.3𝒩(𝑥|7,1) 0.7𝒩(6|5,1) 0.3𝒩(6|7,1) π1=0.7 𝛾𝑛 1 = 0.7𝒩 6 5,1 0.7𝒩 6 5,1 + 0.3𝒩(6|7,1) 寄与率γの計算方法 𝜃 1 = 𝜋 𝑘 1 , 𝝁 𝑘 1 , 𝜮 𝑘 1 𝑘=1 𝐾 𝜋 𝑘 (𝑡+1) = 𝑁𝑘 𝑁 , 𝑁𝑘 = 𝑛=1 𝑁 𝛾𝑛 𝑘 𝝁 𝒌 (𝒕+𝟏) = 1 𝑁𝑘 𝑛=1 𝑁 𝛾𝑛 𝑘 𝒙 𝒏 𝜮 𝒌 (𝒕+𝟏) = 1 𝑁𝑘 𝑛=1 𝑁 𝛾𝑛 𝑘 𝒙 𝒏 − 𝝁 𝒌 (𝒕+𝟏) 𝒙 𝒏 − 𝝁 𝒌 (𝒕+𝟏) 𝑇 各ガウス分布のパラメータを仮設定する 特徴点ごとに各分布への寄与率を計算 寄与率を盛り込んでパラメータを不偏推定 𝛾𝑛 𝑘 = 𝑝 𝑘 𝑥 𝑛, 𝜃(𝑡) = 𝜋 𝑘 𝑡 𝒩 𝒙 𝒏 𝝁 𝑘 𝑡 , 𝜮 𝑘 𝑡 𝑗=1 𝐾 𝜋𝑗 𝑡 𝒩 𝒙 𝒏 𝝁 𝑗 𝑡 , 𝜮𝑗 𝑡
- 9. 4.2.2.1 GMMスーパーベクトル KL距離＝2つの異なる確率密度関数の類似度 （厳密には距離ではない，pからqと，qからpへの距離が異なる） 二つの画像の類似度は，２つの画像の対応するガウス分布ごとにKL を計算して，混合比を重みとして総和をとる 𝐾𝐿 ≤ 1 2𝑘=1 𝐾 𝜋 𝑘 𝝁 𝑘 𝑎 − 𝝁 𝑘 𝑏 𝑇 𝜮 𝑘 −1 𝝁 𝑘 𝑎 − 𝝁 𝑘 𝑏 類似度（カーネル関数） 𝑘 𝜇 𝑘 𝑎 , 𝜇 𝑘 𝑏 = 𝜋 𝑘 𝝁 𝑘 𝑎 𝑇 𝜮 𝑘 −1 𝝁 𝑘 𝑏 スーパーベクトル 𝜐 = 𝝁1, 𝝁2, ⋯ , 𝝁 𝐾 𝑇 𝝁 𝑘 = 𝜋 𝑘Σ 𝑘 −1/2 𝝁 𝑘 画像距離 𝜐 𝑎 , 𝜐 𝑏 = 𝜐 𝑎 𝑇 𝜐 𝑏 画像a 画像b KL計算 KL計算
- 10. 4.2.2.2 フィッシャーベクトル𝜕 𝜕𝜇 𝑓(𝑥|𝜇, 𝜎): 尤度の偏微分 𝜇をわずかに移動すると，尤度がどれくらい増加するか =>密度関数の勾配の強さを表す（分散に似た尺度） 対数尤度で勾配ベクトルをとる 𝒄 𝜽, 𝒙 = 𝛻𝜃 log 𝑓 𝑥 𝜇, 𝜎 = 𝜕 𝜕𝜇 log𝑓 𝑥 𝜇, 𝜎 , 𝜕 𝜕𝜎 log𝑓 𝑥 𝜇, 𝜎 𝑇 𝜇 𝑥 𝑭 = 𝔼 𝑥 𝑐 𝜽, 𝒙 𝑐 𝜽, 𝒙 𝑻 = 𝔼 𝑥 𝜕 𝜕𝜇 log𝑓 𝑥 𝜇, 𝜎 2 𝔼 𝑥 𝜕 𝜕𝜇 log𝑓 𝑥 𝜇, 𝜎 𝜕 𝜕𝜎 log𝑓 𝑥 𝜇, 𝜎 𝔼 𝑥 𝜕 𝜕𝜇 log𝑓 𝑥 𝜇, 𝜎 𝜕 𝜕𝜎 log𝑓 𝑥 𝜇, 𝜎 𝔼 𝑥 𝜕 𝜕𝜎 log𝑓 𝑥 𝜇, 𝜎 2 フィッシャーカーネル：𝑘 𝒙1, 𝒙2 = 𝑐 𝜽, 𝒙1 𝑇 𝑭−1 𝑐 𝜽, 𝒙2 = 𝑐 𝜽, 𝒙 𝑛 𝑇 𝑐 𝜽, 𝒙 𝑛 𝒄 𝜽, 𝒙 𝑛 = 𝐹−1/2 𝒄(𝜽, 𝒙 𝑛) フィッシャーベクトル 𝝊 = 𝑛=1 𝑁 𝒄( 𝜽, 𝒙 𝑛) フィッシャー情報量行列
- 11. 4.2.2.5 VLAD GMMでも混合係数と共分散行列を無視して，平均値のみに着目する特徴点 各コンポーネント（ガウス分布の峰）ℛ 𝑘ごとにコードブック𝑏𝑘と特徴点との差 の総和𝑣 𝑘を計算する 𝑣 𝑘 = 𝑥∈ℛ 𝑘 𝑥 − 𝑏 𝑘 スーパーベクトル 𝑣 = 𝑣1 𝑇 , 𝑣2 𝑇 , ⋯ , 𝑣 𝐾 𝑇 𝑇 もしくは正規化 𝑣 = 𝑣1 𝑇 𝑣1 2 , 𝑣2 𝑇 𝑣2 2 , ⋯ , 𝑣2 𝑇 𝑣 𝐾 2 𝑇
- 12. 4.2.2.5 VLAT GMMでも混合係数を無視して，平均値と共分散行列に着目する特徴点 各コンポーネント（ガウス分布の峰）ℛ 𝑘ごとに平均からの二乗距離と共分散 行列Σ𝑘との差の総和𝑇𝑘を計算する 𝑇𝑘 = 𝑥∈ℛ 𝑘 ( 𝑥 − 𝜇 𝑘 𝑥 − 𝜇 𝑘 𝑇 − Σ 𝑘) スーパーベクトル 𝑣 = 𝑣𝑒𝑐 𝑇1 𝑇, 𝑣𝑒𝑐 𝑇2 𝑇, ⋯ , 𝑣𝑒𝑐 𝑇 𝐾 𝑇 𝑇
- 13. 4.2.3.2 Log-Euclidean計量 ガウス分布の共分散行列Sは正定値 正定値行列Sは固有値分解可能 𝑆 =𝑈Λ𝑈 𝑇 ∈ ℝ 𝐷×𝐷 exp 𝑆 = 𝑈𝑑𝑖𝑎𝑔(exp(𝜆1), exp(𝜆2), ⋯ , exp(𝜆 𝐷))𝑈 𝑇 log 𝑆 = 𝑈𝑑𝑖𝑎𝑔(log(𝜆1), log(𝜆2), ⋯ , log(𝜆 𝐷))𝑈 𝑇 ユークリッド距離のように扱える 𝐷 𝑆1, 𝑆2 = log 𝑆1 − log(𝑆2) → 𝜇も log Σ もユークリッド平面で取り扱いが可能になる