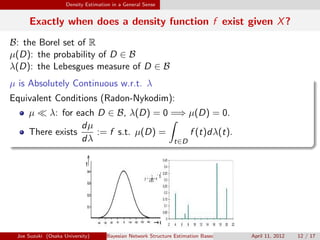
The document discusses Bayesian network structure estimation using Bayesian/MDL criteria for datasets containing both discrete and continuous variables. It outlines the challenges posed by mixed-variable structures in density estimation and presents methodologies to compute probabilistic dependencies without assuming purely discrete or continuous distributions. Future work aims to develop structure estimation modules in realistic settings leveraging the proposed universal measures.








![Problem
Why can Pn
be replaced by Qn
?
.
Qn: a universal coding measure w.r.t. A
..
......
−
1
n
log Qn
(xn
) → H for any P
∑
xn∈An
Qn
(xn
) ≤ 1
such as Qn
(xn
) := 2−Lφ(xn)
if φ is universal
Shannon-McMillan-Breiman: for any P,
−
1
n
log Pn
(xn
) =
1
n
n∑
i=1
{− log P(xi )} → E[− log P(X)] = H
.
Universality
..
......
1
n
log
Pn(xn)
Qn(xn)
→ 0
Joe Suzuki (Osaka University) Bayesian Network Structure Estimation Based on the Bayesian/MDL Criteria When Both DApril 11, 2012 8 / 17](https://image.slidesharecdn.com/2012-4-9-170405231356/85/Bayesian-network-structure-estimation-based-on-the-Bayesian-MDL-criteria-when-both-discrete-and-continuous-variables-are-present-10-320.jpg)