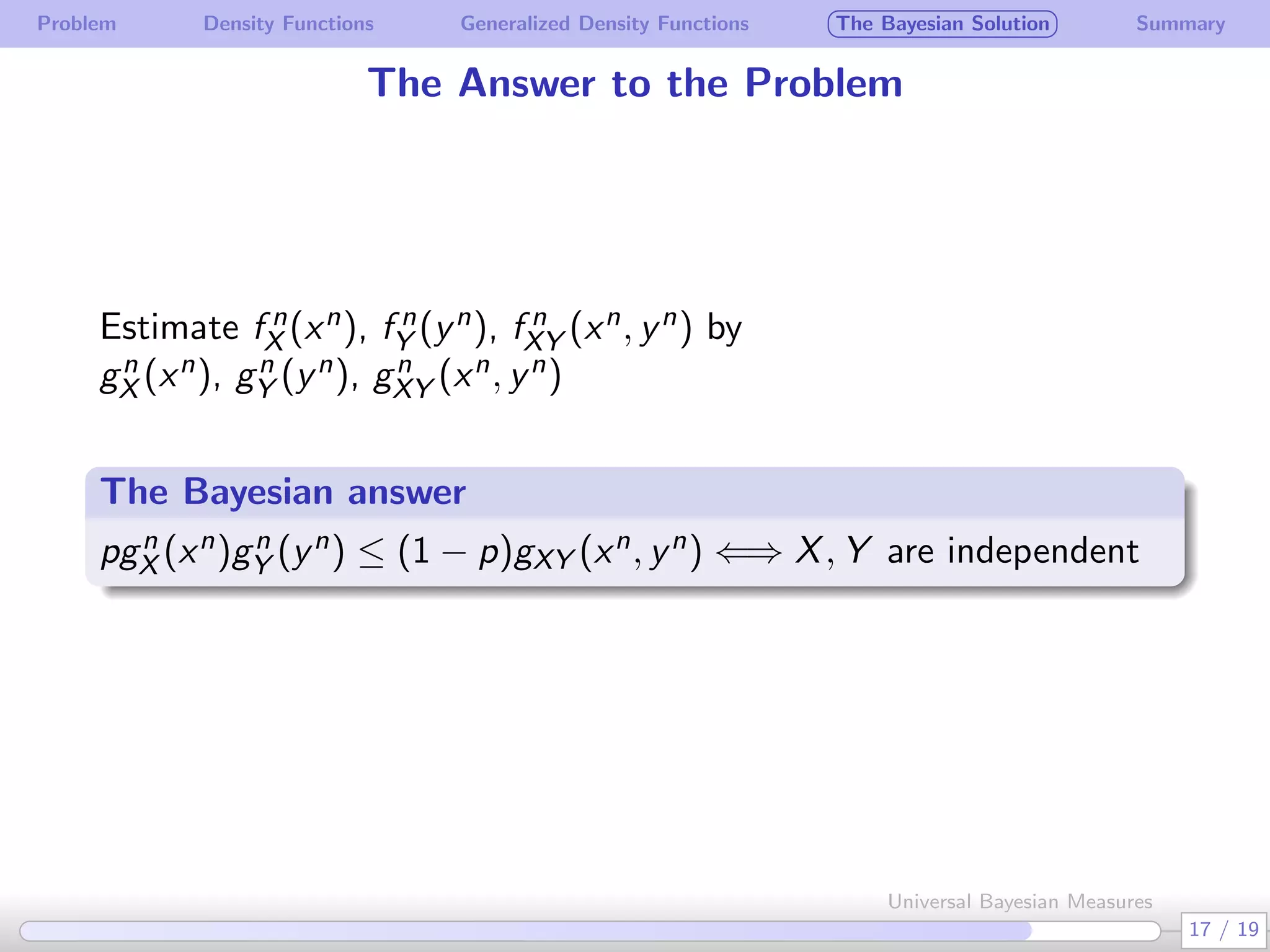
The document discusses generalizing Bayesian measures to situations where random variables may be neither discrete nor continuous. It defines generalized density functions that allow estimating probabilities without assuming an underlying distribution. A main theorem states that universal Bayesian measures gn can estimate densities fn such that the log ratio of fn/gn approaches 0 as n increases, for any stationary ergodic distribution. This generalizes the Bayesian solution to testing independence of random variables without requiring a known distribution.

1. Problem Density Functions Generalized Density Functions The Bayesian Solution Summary
Universal Bayesian Measures
Joe Suzuki
Osaka University
IEEE International Symposium on Information Theory
Istanbul, Turky
July 8, 2013
1 / 19
Universal Bayesian Measures

2. Problem Density Functions Generalized Density Functions The Bayesian Solution Summary
Given n examples, identify whether X, Y are
independent or not
(x1, y1), · · · , (xn, yn) ∼ (X, Y ) ∈ {0, 1} × {0, 1}
p: a prior probability that X, Y are independent
The Bayesian answer
Consider weight W over θ to compute
Qn
(xn
) :=
∫
P(xn
|θ)dW (θ) , Qn
(yn
) :=
∫
P(yn
|θ)dW (θ)
Qn
(xn
, yn
) :=
∫
P(xn
, yn
|θ)dW (θ)
pQn(xn)Qn(yn) ≥ (1 − p)Qn(xn, yn) ⇐⇒ X, Y are independent
2 / 19
Universal Bayesian Measures

3. Problem Density Functions Generalized Density Functions The Bayesian Solution Summary
Problem: what if X, Y are arbitrary random variables?
(Ω, F, P): probability space
B: the Borel set of R
X is a random variable
.
.
X : Ω → R is F-measurable
(D ∈ B =⇒ {ω ∈ Ω|X(ω) ∈ D} ∈ F)
X, Y may be either
discrete
contunuous
none of them
3 / 19
Universal Bayesian Measures

4. Problem Density Functions Generalized Density Functions The Bayesian Solution Summary
What Qn
is qualified to be an alternative to Pn
?
True θ = θ∗ is not available
.
.
Pn(xn) = P(xn|θ∗), Pn(yn) = P(yn|θ∗)
Pn(xn, yn) = Pn(xn, yn|θ∗)
Qn
(xn
) :=
∫
P(xn
|θ)dW (θ) , Qn
(yn
) :=
∫
P(yn
|θ)dW (θ)
Qn
(xn
, yn
) :=
∫
P(xn
, yn
|θ)dW (θ)
4 / 19
Universal Bayesian Measures

5. Problem Density Functions Generalized Density Functions The Bayesian Solution Summary
Example: Bayes Codes
c: the # of ones in xn
θ: the prob. of ones
P(xn
|θ) = θc
(1 − θ)n−c
a, b > 0
w(θ) ∝
1
θa(1 − θ)b
For each xn = (x1, · · · , xn) ∈ {0, 1}n,
Qn
(xn
) :=
∫
w(θ)P(xn
|θ)dθ =
∏c−1
j=0 (j + a) ·
∏n−c−1
k=0 (k + b)
∏n−1
i=0 (i + a + b)
5 / 19
Universal Bayesian Measures

6. Problem Density Functions Generalized Density Functions The Bayesian Solution Summary
Universal Coding/Measures
If we choose
a = b = 1/2
(Krichevsky-Trofimov) and xn is i.i.d. emitted by
Pn
(xn
|θ) =
n∏
i=1
P(xi ) , P(xi ) = θ, 1 − θ
then, for any P, almost surely,
−
1
n
log Qn
(xn
) → H :=
∑
x∈A
−P(x) log P(x)
From Shannon McMillian Breiman, for any P,
−
1
n
log Pn
(xn
|θ) =
1
n
n∑
i=1
− log P(xi ) → E[− log P(xi )] = H
6 / 19
Universal Bayesian Measures

7. Problem Density Functions Generalized Density Functions The Bayesian Solution Summary
Why Pn
can be replaced by Qn
if n is large ?
For any P, almost surely,
1
n
log
Pn(xn)
Qn(xn)
→ 0 (1)
Qn: a universal Bayesian measure for A
.
What are Qn and (1) in the general settings ?
7 / 19
Universal Bayesian Measures

8. Problem Density Functions Generalized Density Functions The Bayesian Solution Summary
Suppose a density function exists for X
A: the range of X
A0 := {A}
Aj+1 is a refinement of Aj
Example 1: if A = [0, 1), the sequence can be A0 = {[0, 1)},
A1 = {[0, 1/2), [1/2, 1)}
A2 = {[0, 1/4), [1/4, 1/2), [1/2, 3/4), [3/4, 1)}
. . .
Aj = {[0, 2−(j−1)), [2−(j−1), 2 · 2−(j−1)), · · · , [(2j−1 − 1)2−(j−1), 1)}
. . .
sj : A → Aj (quantization, x ∈ a ∈ Aj =⇒ sj (x) = a)
λ : R → B (Lebesgue measure, a = [b, c) =⇒ λ(a) = c − b)
Qn
j : a universal Bayesian measure for Aj
8 / 19
Universal Bayesian Measures

9. Problem Density Functions Generalized Density Functions The Bayesian Solution Summary
If (sj (x1), · · · , sj (xn)) = (a1, · · · , an),
gn
j (xn
) :=
Qn
j (a1, · · · , an)
λ(a1) · · · λ(an)
f n
j (xn
) := fj (x1) · · · fj (xn) =
Pj (a1) · · · Pj (an)
λ(a1) . . . λ(an)
For {ωj }∞
j=1:
∑
ωj = 1, ωj > 0, gn
(xn
) :=
∞∑
j=1
ωj gn
j (xn
)
For any f and {Aj } s.t. h(fj ) → h(f ) as j → ∞, almost surely
1
n
log
f n(xn)
gn(xn)
→ 0 (2)
B. Ryabko. IEEE Trans. on Inform. Theory, 55, 9, 2009.
9 / 19
Universal Bayesian Measures

10. Problem Density Functions Generalized Density Functions The Bayesian Solution Summary
Our Goal: what are they generalized into?
. 1 if the random variable takes finite values:
1
n
log
Pn
(xn
)
Qn(xn)
→ 0 (1)
for any Pn
.
2 if a density function exists:
1
n
log
f n
(xn
)
gn(xn)
→ 0 (2)
for any f n
and {Aj } satisfies h(fj ) → h(f ) as j → ∞
10 / 19
Universal Bayesian Measures

11. Problem Density Functions Generalized Density Functions The Bayesian Solution Summary
Exactly when does density function exist?
B: the Borel sets of R
µ(D): the prob. of D ∈ B
When a density function exists
.
The following are equivalent (µ ≪ λ):
for each D ∈ B, λ(D) = 0 =⇒ µ(D) = 0
∃ B-measurable
dµ
dλ
:= f s.t. µ(D) =
∫
D
f (t)dλ(t)
f is the density function (w.r.t. λ).
11 / 19
Universal Bayesian Measures

12. Problem Density Functions Generalized Density Functions The Bayesian Solution Summary
Density Functions in a General Sense
Radon-Nikodum’s Theorem
.
.
The following are equivalent (µ ≪ η):
for each D ∈ B, η(D) = 0 =⇒ µ(D) = 0
∃ B-measurable
dµ
dη
:= fη s.t. µ(D) =
∫
D
fη(t)dη(t)
fη is the density function w.r.t. η.
Example 2: µ({h}) > 0, η({h}) :=
1
h(h + 1)
, h ∈ B := {1, 2, · · · }
µ ≪ η
µ(D) =
∑
h∈D∩B
fη(h)η({h})
dµ
dη
(h) = fη(h) =
µ({h})
η({h})
= h(h + 1)µ({h})
12 / 19
Universal Bayesian Measures

13. Problem Density Functions Generalized Density Functions The Bayesian Solution Summary
B1 := {{1}, {2, 3, · · · }}
B2 := {{1}, {2}, {3, 4, · · · }}
. . .
Bk := {{1}, {2}, · · · , {k}, {k + 1, k + 2, · · · }}
. . .
tk : B → Bk (quantization, y ∈ b ∈ Bk =⇒ tk(y) = b)
If (tk(y1), · · · , tk(yn)) = (b1, · · · , bn),
gn
η,k(yn
) :=
Qn
k (b1, · · · , bn)
η(b1) · · · η(bn)
, gn
η (yn
) :=
∞∑
k=1
ωkgn
η,k(yn
)
For any fη and {Bk} s.t. h(fη,k) → h(fη) , almost surely
1
n
log
f n
η (yn)
gn
η (yn)
→ 0 (3)
gn(yn)
∏n
i=1 ηn({yi }) estimates P(yn) = f n
η (yn)
∏n
i=1 ηn({yi })
13 / 19
Universal Bayesian Measures

14. Problem Density Functions Generalized Density Functions The Bayesian Solution Summary
In the general case
µn
(Dn
) :=
∫
D
f n
η (yn
)dηn
(yn
)
νn
(Dn
) :=
∫
D
gn
η (yn
)dηn
(yn
)
f n
η (yn)
gn
η (yn)
=
dµn
dηn
(yn
)/
dνn
dηn
(yn
) =
dµn
dνn
(yn
)
D(µ||ν) :=
∫
dµ log
dµ
dν
h(fη) :=
∫
−f n
η (yn
) log f n
η (yn
)dη(yn
)
= −
∫
dµ
dη
(yn
) log
dµ
dη
(yn
) · dη(yn
) = −D(µ||η)
14 / 19
Universal Bayesian Measures

15. Problem Density Functions Generalized Density Functions The Bayesian Solution Summary
Main Theorem
Theorem
.
With probability one as n → ∞
1
n
log
dµn
dνn
(yn
) → 0
for any stationary ergodic µn and {Bk} such that
D(µk||η) → D(µ||η) as k → ∞
15 / 19
Universal Bayesian Measures

16. Problem Density Functions Generalized Density Functions The Bayesian Solution Summary
Joint Density Functions
Example 3: A × B (based on Examples 1,2)
µ ≪ λη
A0 × B0 = {A} × {B} = {[0, 1)} × {{1, 2, · · · }}
A1 × B1
A2 × B2
. . .
Aj × Bk
. . .
(sj , tk) : A × B → Aj × Bk
If {Aj × Bk} satisfies fλη,jk → fλη, for any fλη, almost surely, we
can construct gn
λη s.t.
1
n
log
f n
λη(xn, yn)
gn
λη(xn, yn)
→ 0 (4)
16 / 19
Universal Bayesian Measures

17. Problem Density Functions Generalized Density Functions The Bayesian Solution Summary
The Answer to the Problem
Estimate f n
X (xn), f n
Y (yn), f n
XY (xn, yn) by
gn
X (xn), gn
Y (yn), gn
XY (xn, yn)
The Bayesian answer
.
.
pgn
X (xn)gn
Y (yn) ≤ (1 − p)gXY (xn, yn) ⇐⇒ X, Y are independent
17 / 19
Universal Bayesian Measures

18. Problem Density Functions Generalized Density Functions The Bayesian Solution Summary
The General Bayesian Solution
Givem n examples zn and prior {pm} over models m = 1, 2, · · · ,
compute gn
(zn
|m) for each m = 1, 2, · · ·
find the model m maxmizing pmg(zn
|m)
18 / 19
Universal Bayesian Measures

19. Problem Density Functions Generalized Density Functions The Bayesian Solution Summary
Summary and Discussion
Bayesian Measure
.
.
Generalization without assuming Discrete or Continuous
Universality of Bayes/MDL in the generalized sense
Many Applications
Bayesian network structure estimation (DCC 2012)
The Bayesian Chow-Liu Algorithm (PGM 2012)
Markov order estimation even when {Xi } is continuous
19 / 19
Universal Bayesian Measures