The document discusses constitutive equations and materials behavior. It provides the following key points:
1. Constitutive equations describe the relationship between stress and strain for a material and can distinguish between solids and fluids, as well as different types of solids.
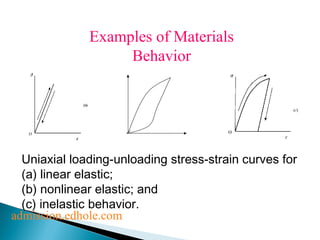
2. For elastic solids, stress is proportional to strain, following Hooke's law. The proportionality constant is the elastic modulus. Materials exhibit linear or non-linear elastic behavior.
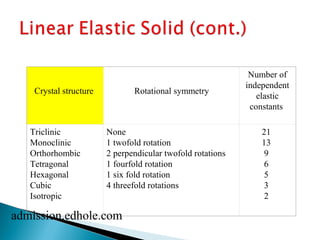
3. Isotropic materials have properties that are identical in all directions, allowing their behavior to be defined by just two independent constants in the constitutive equation.














![(b) Inverting the relations, can e -s be written as:
E v
= + - -
1 1
[( ) s s
]
[( ) ]
( )
E G
11 11 22
Y
E v
= + - -
1 1
s s
22 22 11
E v
v v
E
v v
E
= + =
Y
Y
2 2
2 1
12 12
12
s s
(c) Navier's equation for displacement can be written as:
E
E
Y ( ) u +
Y
u + r
b = ( i j
=
)
2 1 +
v
i , jj
( 0 , 1,22 1 + v )( 1 -
2 v
) j , ji i
admission.edhole.com](https://image.slidesharecdn.com/b-141022014230-conversion-gate02/85/B-tech-admission-in-india-16-320.jpg)

![If is Cauchy tensor and is small strain tensor, then in general,
s ij Eij
sij=CijklEkl
Cijkl
where is a fourth order tensor, since T and E are second order
tensors. is called elasticity tensor. The values of these components
with respect to the primed basis ei’ and the unprimed basis ei are related by
the transformation law
ijkl mi ni rk sl mnrs C¢ = Q Q Q Q C
However, we know that E k l = E l k and then
Cijkl = C jikl = Ciklk [C] 4´4
sij=sji
We have symmetric matrix with 36 constants, If
elasticity is a unique scalar function of stress and strain, strain energy is given by
dU= sijdEkl or U= sijEij
Then sij = ¶U
¶Eij
ÞCijkl =Cklij
ÞNumber of independent constants=21
Cijkl
admission.edhole.com](https://image.slidesharecdn.com/b-141022014230-conversion-gate02/85/B-tech-admission-in-india-18-320.jpg)