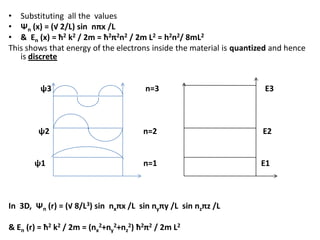
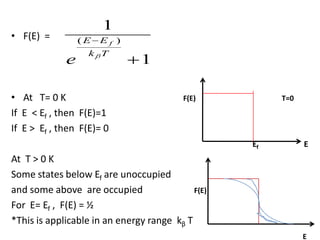
1) Sommerfield's quantum free electron theory treats electrons inside a solid as particles confined in a box. This leads to quantized, discrete energy levels for the electrons described by the Schrodinger equation. 2) The highest filled energy level at 0K is called the Fermi level, and its energy is the Fermi energy. In 3D, the Fermi energy and wave vector depend on the electron density. 3) The density of states and Fermi-Dirac distribution describe the probability of electrons occupying different energy levels at different temperatures. The average electron energy is calculated based on these concepts.

1. Quantum free electron theory(Sommerfield)
• Particles of micro dimension like the electrons are studied under
quantum physics
• moving electrons inside a solid material can be associated with
waves with a wave function ψ(x) in one dimension (ψ(r) in 3D)
• Hence its behaviors can be studied with the Schrödinger's
equation (1D)
For a free particle V=0, hence the equation reduces to
E
With
0)()(
2)(
22
2
xVE
m
x
x

,0)(
)( 2
2
2
xk
x
x
2
,
2
,
2
22
2
2
h
m
k
Eor
mE
k



K Ef

2. Sommerfield’s model
• As the freely moving electrons can not escape the surface of the
material, they may be treated as particles confined (trapped)in a
box
• Hence, V(x) =0, for 0<x<L . e-
= ∞, for x=0 & x=L V(x)
0 L x
Sch’s equation ,
Solution of the equation can be obtained as
ψ(x) = A sin kx + B cos kx
From boundary conditions , at x=o & x=L , ψ(x)=0,
we can get B=0 and k= ± nπ / L ,
Putting the normalization condition we get A=
0)(
2)(
22
2
x
mE
x
x

P= 0
Ψ= 0
P= 0
Ψ= 0
L
2

3. • Substituting all the values
• Ψn (x) = (√ 2/L) sin nπx /L
• & En (x) = ħ2 k2 / 2m = ħ2π2n2 / 2m L2 = h2n2/ 8mL2
This shows that energy of the electrons inside the material is quantized and hence
is discrete
ψ3 n=3 E3
ψ2 n=2 E2
ψ1 n=1 E1
In 3D, Ψn (r) = (√ 8/L3) sin nxπx /L sin nyπy /L sin nzπz /L
& En (r) = ħ2 k2 / 2m = (nx
2+ny
2+nz
2) ħ2π2 / 2m L2

4. Fermi Level and Fermi Energy:
• Electrons are fermions or Fermi particles, which obey Pauli’s
exclusion principle
• At 0K temperature the highest filled energy level is called the
“Fermi Level” & the energy possessed by the electrons in that
level is “Fermi Energy”
• Ef = ħ2 kf
2 / 2m or kf = (2mEf / ħ2 )1/2
• In 3D electrons will fill up the k-space with one state
accommodating 2 electrons each ( ↑↓)
• If N is the total no. of electrons & is large , electrons will occupy
a sphere of radius kf , then highest occupied state
nf = N/2
From uncertainty principle electron states
∆x ∆p =h or, ∆x ħ∆k = h
Or, L (h/2π) ∆k = h or, ∆k = 2π / L
kx
ky
kf

5. • state in k-space of radius kf =
• = Kf
3 L3 / 6π2
• Hence no. of electrons ‘N’ = 2 X ( Kf
3 L3 / 6π2 )
•
• So, kf = {3π2 (N/ V) }1/3
• where n = electron density = N/V = 1/ V (kf
3 V / 3π2 )
• Or, n=
3
3
2
3
4
L
k f
N = kf
3 V / 3π2
kf = (3π2 n) 1/3
2
3
2
3
22
2
3
1
fE
m


6. • at 0 K, the fermi energy
• Ef (0) = ħ2 kf
2 / 2m
• = ħ2 / 2m ( 3π2n)2/3
• Ef(0) = h2/ 8m (3n/ π ) 2/3
• Fermi velocity vf = ħkf / m = ħ /m (3π2n) 1/3
Density of States: Z(E) = no. of states per unit energy range
per unit volume of the metal
No. of free electrons within energy value ‘E’
= no. of states within the sphere of radius ‘k’ in k-space
= N(E) = Vk3 / 3π2 = V/ 3π2 ( 2mE/ ħ2)3/2
or , Z(E) = 2
3
222
3
2
3
1
3
)(1

mE
dE
dk
dE
d
dE
EdN
V

7. =
Or, Z(E)=
Z(E)
0 or, Z(E) α E ½
Fermi Dirac distribution function
Distribution of electrons in different energy states is given by Fermi-Dirac
statistics.
Fermi Dirac distribution function F(E) gives the probability of occupation
of an energy level ‘E’, by an electron at temperature ‘T’
2
1
2
3
22
2
32
3
1
E
m

2
1
2
3
22
2
2
1
E
m

E
T=0
Ef

8. • F(E) =
• At T= 0 K F(E) T=0
If E < Ef , then F(E)=1
If E > Ef , then F(E)= 0
Ef E
At T > 0 K
Some states below Ef are unoccupied
and some above are occupied F(E)
For E= Ef , F(E) = ½
*This is applicable in an energy range kβ T
E
1
1
)(
Tk
EE f
e

9. • Average energy of free electrons:
• Av. Energy = total energy of all the electrons in the metal
no. of electrons per unit volume
< E > =
As no. of free electrons per volume, n=
At T = 0 K : upper limit of integration is Ef0 and F(E) is 1
<E0 > =
As n =
n
dEEFEZE
0
)()(.
2
3
2
3
22
0
2
1
2
3
22
2
3
1
.1.
2
2
1
.
0
f
E
E
m
dEE
m
E
f


2
3
2
3
22
2
3
1
fE
m

0
)(.)( EFdEEZ

10. • <E0> = or
For T > 0 K ( In a metal some states above fermi level are
occupied at T > 0K)
• < E T> =
=
• Where, Ef (T) =
2
3
2
5
0
0
3
1
.
2
5
2
1
f
f
E
E <E0> = 3/5 Ef0
2
3
2
3
22
0
)(
2
1
2
3
22
2
3
1
1
1
.
2
2
1
.
f
Tk
EE
E
m
dE
e
E
m
E f


2
2
0
0
12
5
1
fE
Tk
E
2
2
0
0
12
1
f
f
E
Tk
E

11. Specific heat in quantum free electron theory
• In classical theory , Specific heat ‘C’ of the electron gas
C = = = 3/2 kβ
• Molar specific heat =
Hence, thermal conductivity K = 1/2 n kβ vth λ
=1/3 C vth λ
In quantum theory, av. Energy of a free electron,
For an electron density ‘n’
specific heat =
Is found to be agreeing with experimental result
C = n C = 3/2 n kβ
0
0 2
222
12
5
1
5
3
f
f
E
Tk
EE
C = n d<E>/ dT = π2nkβ
2T / 2Ef0
Tk
dT
d
2
3
E
dT
d

12. Lorenz no. in quantum free electron theory
So, thermal conductivity
K = 1/3 (π2nkβ
2T / 2Ef0 ) vth
2 τ
= π2kβ
2nTτ / 3m (as ½ mvth
2 = Ef0 )
So, Weidman – Franz law
K/σ =
=
= L T
In classical theory L = Lorenz no. = 3kβ
2 / 2q2
In quantum theory L = π2kβ
2/ 3q2 = 2.45X 10 -8 WΩ / K2
and agrees well with exptl. result
m
nq
m
nTk
2
22
3
T
q
k
2
22
3