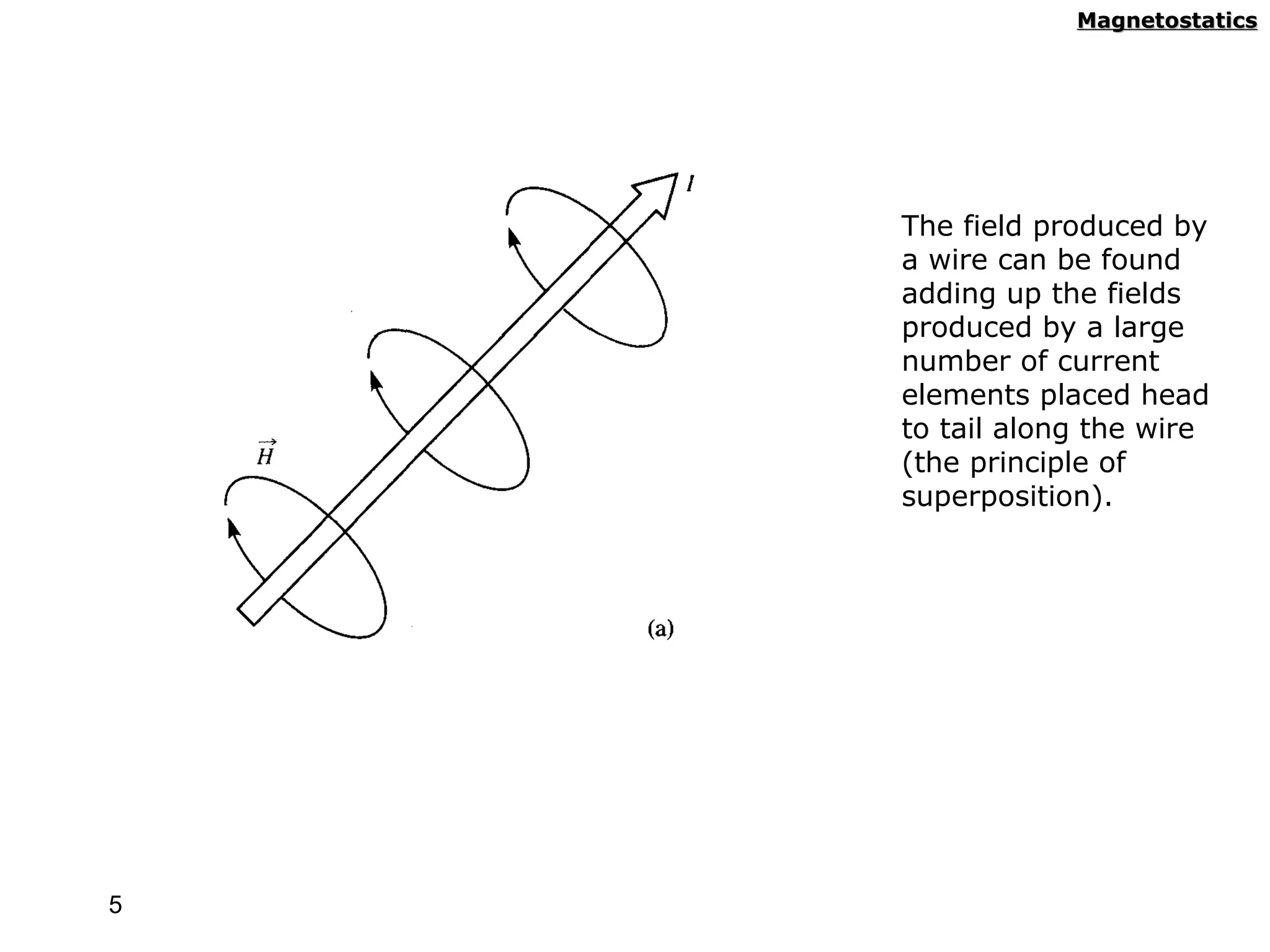
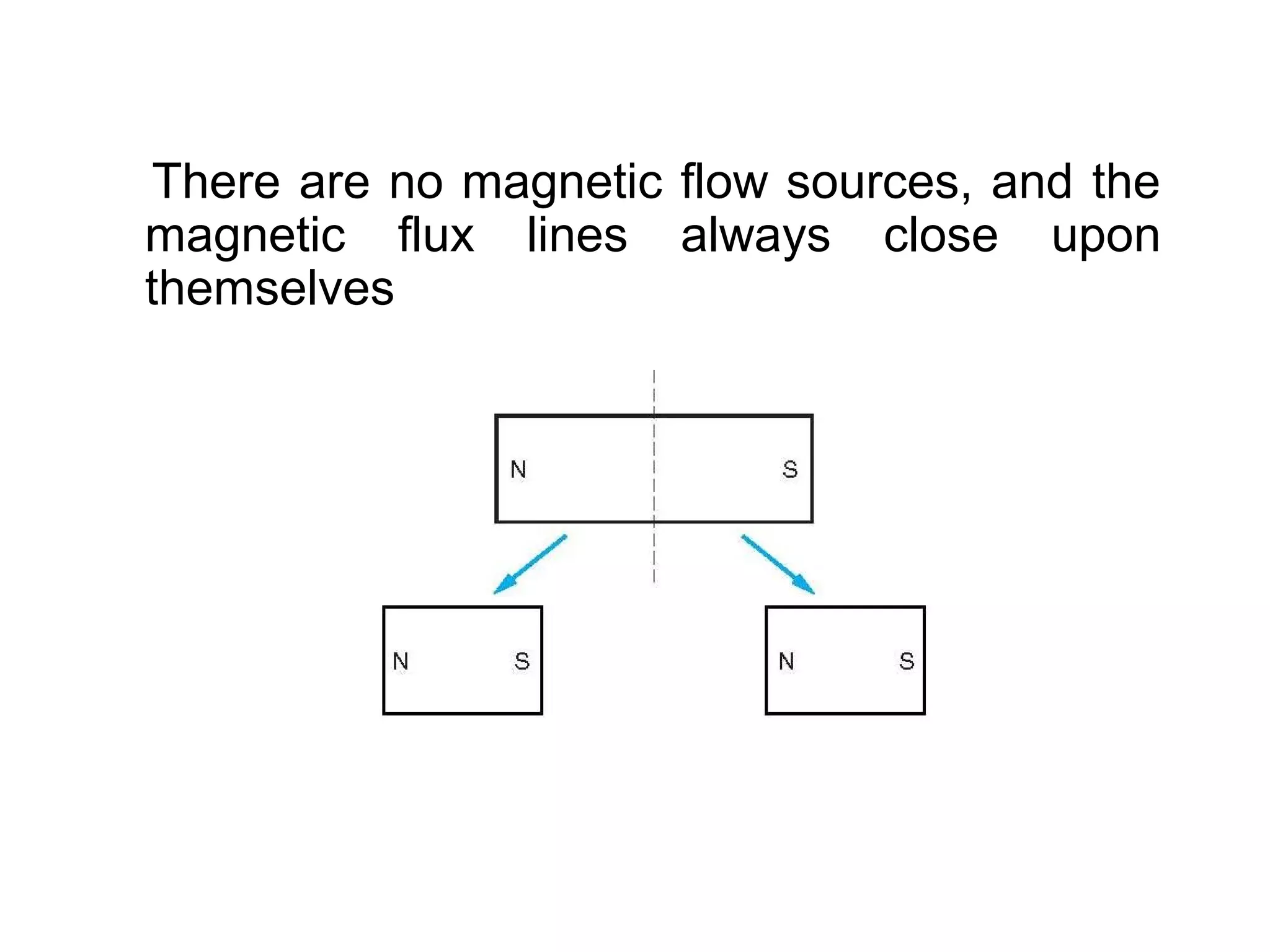
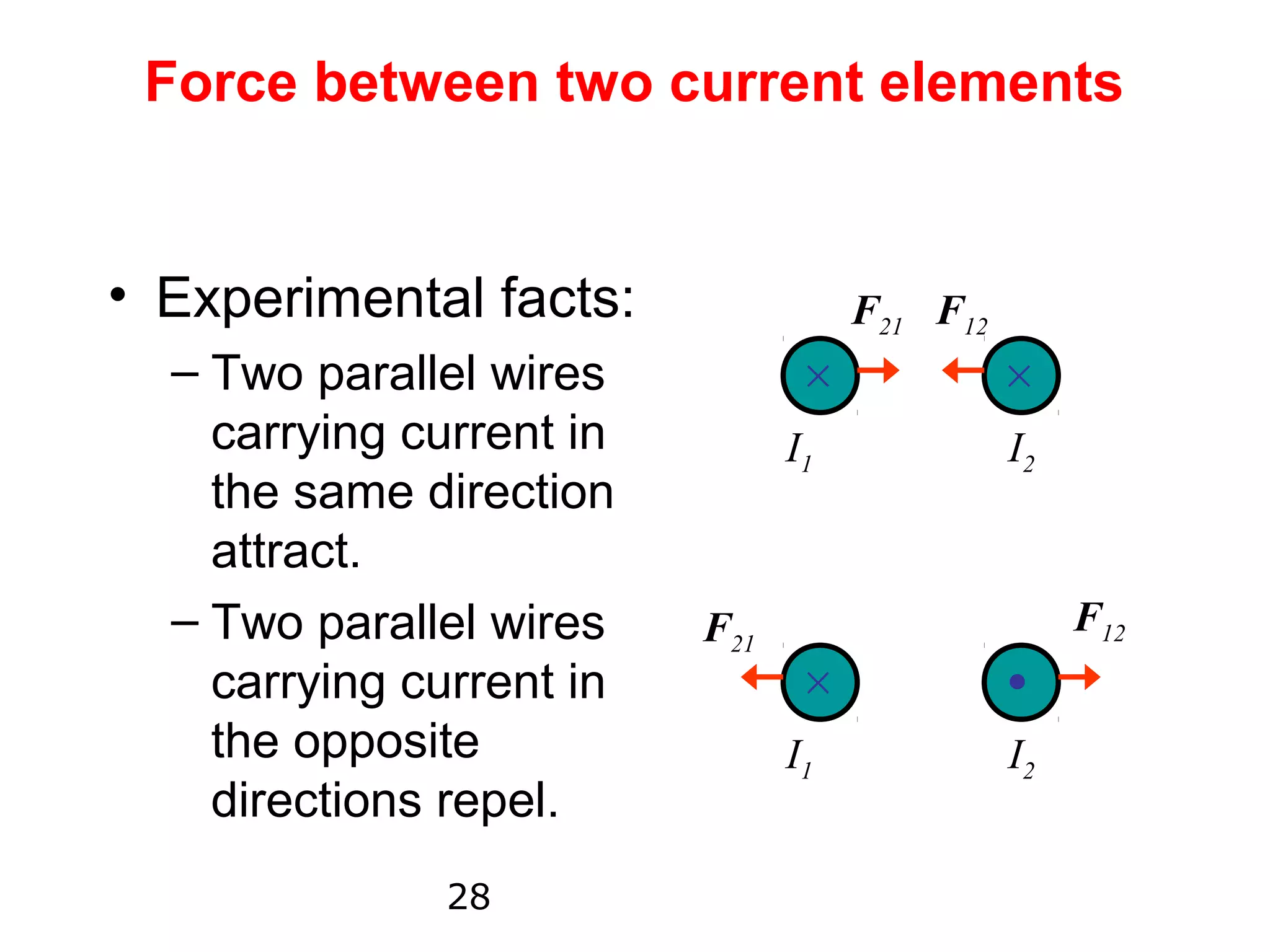
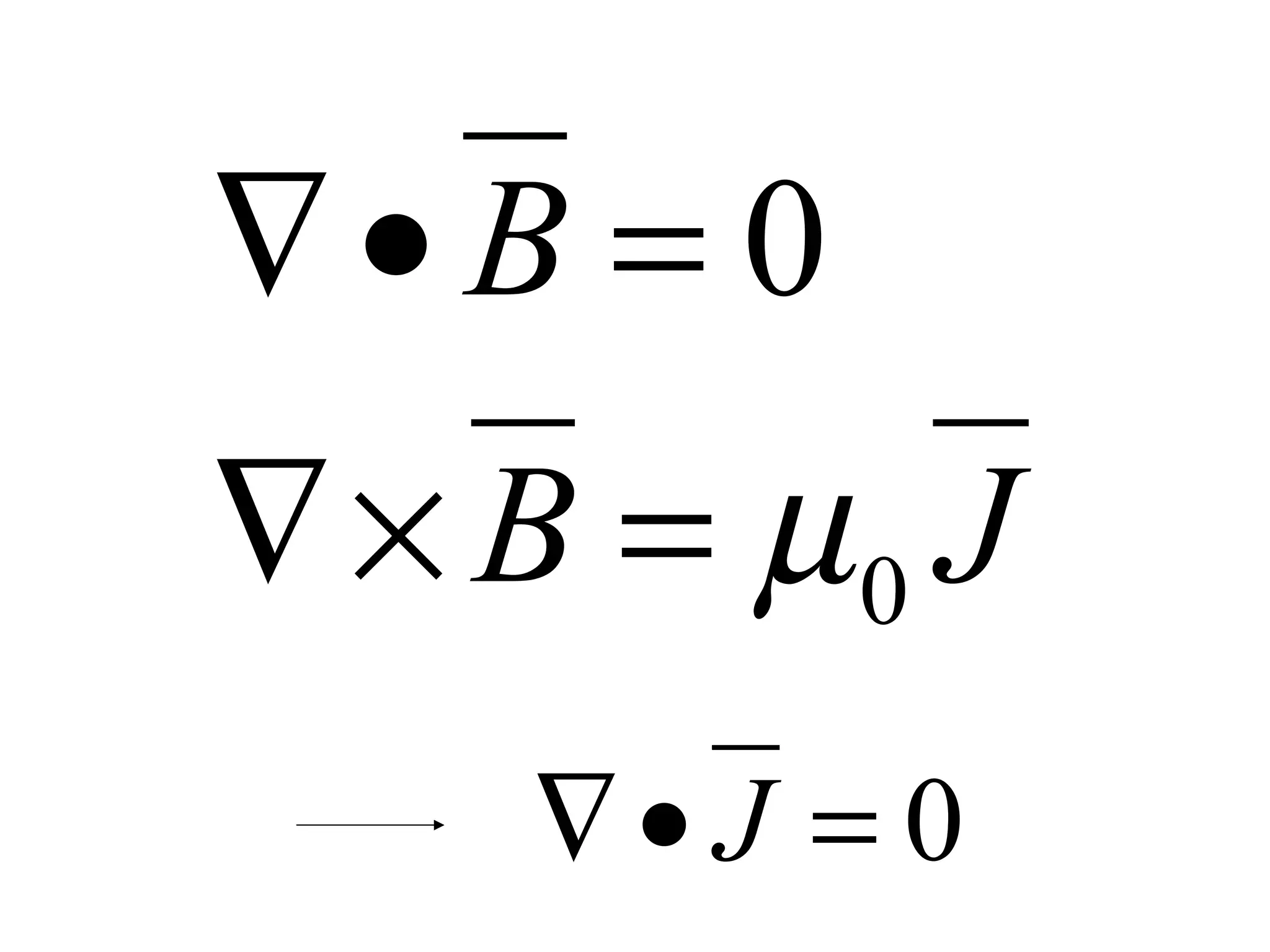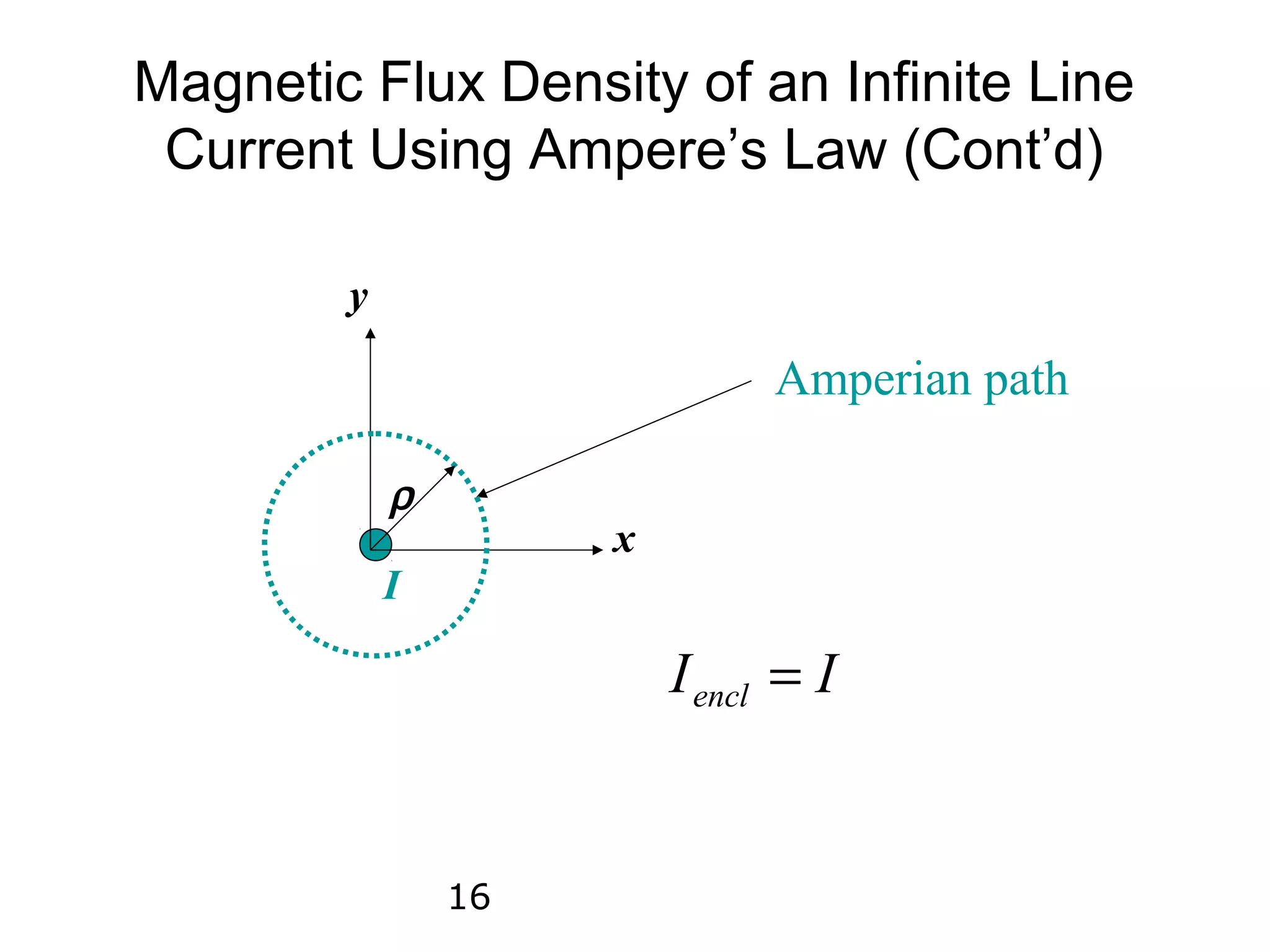
1) Magnetostatic fields are produced when charges move with constant velocity, originating from currents like those in wires. 2) Biot-Savart's law describes the magnetic field produced by a current element, with the field proportional to the current and inversely proportional to the distance. 3) Ampere's law, in integral and differential form, relates the line integral of the magnetic field around a closed path to the total current passing through the enclosed surface.

1. Magnetostatics

2. Magnetostatics
If charges are moving with constant velocity, a static
magnetic (or magnetostatic) field is produced. Thus,
magnetostatic fields originate from currents (for instance,
direct currents in current-carrying wires).
Most of the equations we have derived for the electric fields
may be readily used to obtain corresponding equations for
magnetic fields if the equivalent analogous quantities are
substituted.
2

3. Magnetostatics
Biot – Savart’s Law The magnetic field intensity
dH produced at a point P by
the differential current
element Idl is proportional
to the product of Idl and the
sine of the angle α between
the element and the line
joining P to the element and
is inversely proportional to
Idl sin α the square of the distance R
dH = k
R2 between P and the element.
1
IN SI units, k = 4π , so
Idl sin α
dH = k
4πR 2
3

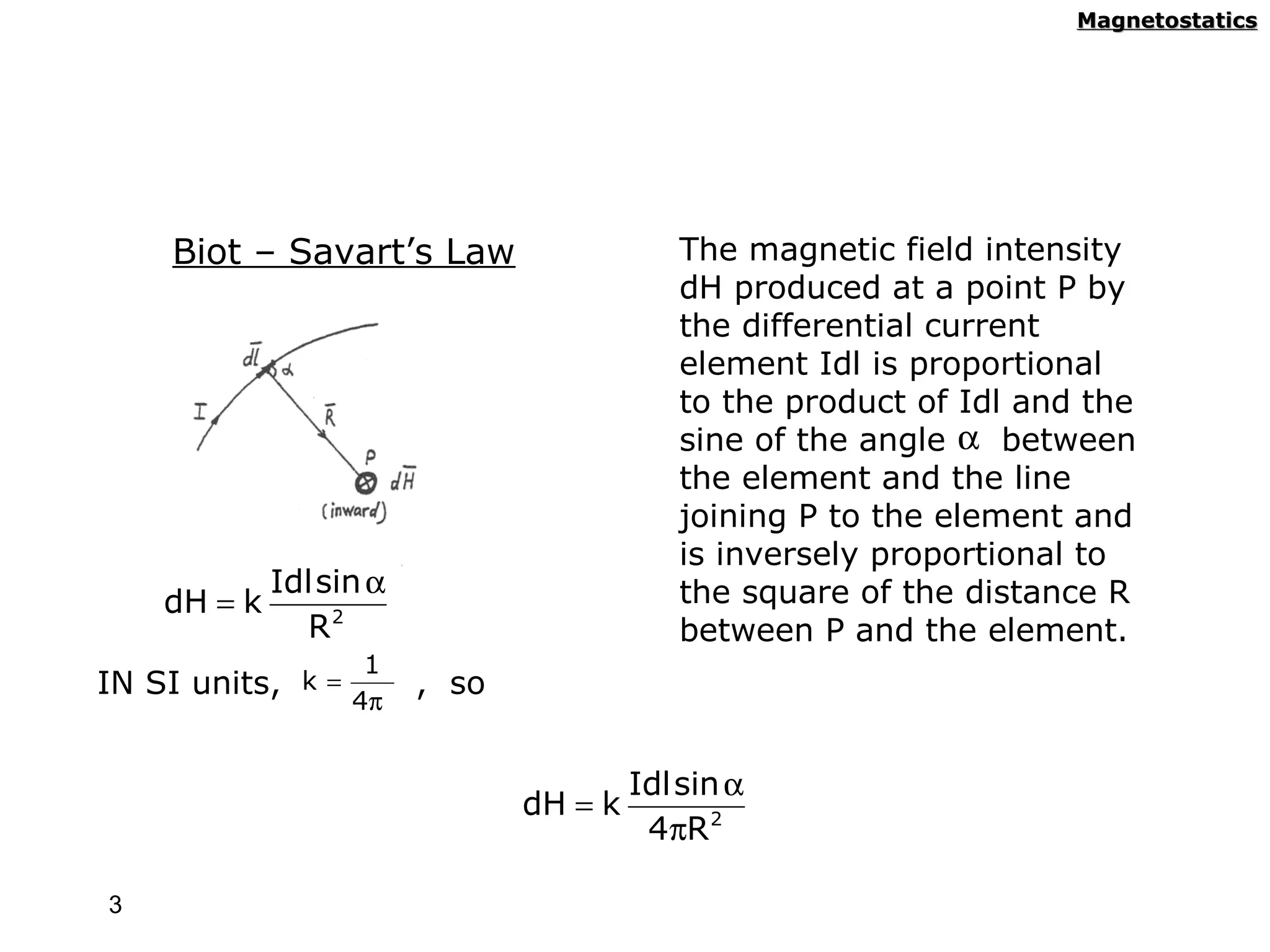
4. Magnetostatics
Using the definition of cross product ( A × B = AB sin θ AB an )
we can represent the previous equation in vector form as
I dl × ar I dl × R
dH = = R= R ar = R
4πR 2 4πR 3 R
The direction of d H can be determined by the right-hand rule
or by the right-handed screw rule.
If the position of the field point is specified by r and the
position of the source point by r ′
I (dl × ar ) I [dl × (r − r ′)]
dH = 2
= 3
4π r − r ′ 4π r − r ′
where er′r is the unit vector directed from the source point to
the field point, and r − r ′ is the distance between these two
points.
4

5. Magnetostatics
The field produced by
a wire can be found
adding up the fields
produced by a large
number of current
elements placed head
to tail along the wire
(the principle of
superposition).
5

6. Types of Current Distributions
• Line current density (current) - occurs for
infinitesimally thin filamentary bodies
(i.e., wires of negligible diameter).
• Surface current density (current per unit
width) - occurs when body is perfectly
conducting.
• Volume current density (current per unit
cross sectional area) - most general.
6

7. Ampere’s Circuital Law in
Integral Form
• Ampere’s Circuit Law states that the line
integral of H around a closed path
proportional to the total current through
the surface bounding the path
C
∫ H ⋅ d l = I enc
7

8. Ampere’s Circuital Law in
Integral Form (Cont’d)
dl By convention, dS is
taken to be in the
dS direction defined by the
S
right-hand rule applied
to dl.
Since volume current
density is the most
I encl = ∫ J ⋅ d s general, we can write
Iencl in this way.
S

9. Applying Stokes’s Theorem to
Ampere’s Law
∫ H ⋅ dl = ∫ ∇× H ⋅ d s
C S
= I encl = ∫ J ⋅d s
S
⇒ Because the above must hold for any
surface S, we must have
Differential form
∇× H = J
of Ampere’s Law
9

10. Ampere’s Law in Differential
Form
• Ampere’s law in differential form implies
that the B-field is conservative outside of
regions where current is flowing.
10

11. Applications of Ampere’s Law
• Ampere’s law in integral form is an integral
equation for the unknown magnetic flux
density resulting from a given current
distribution.
known
∫
C
H ⋅ d l = I encl
unknown
11

12. Applications of Ampere’s Law
(Cont’d)
• In general, solutions to integral equations
must be obtained using numerical
techniques.
• However, for certain symmetric current
distributions closed form solutions to
Ampere’s law can be obtained.
12

13. Applications of Ampere’s Law
(Cont’d)
• Closed form solution to Ampere’s law
relies on our ability to construct a suitable
family of Amperian paths.
• An Amperian path is a closed contour to
which the magnetic flux density is
tangential and over which equal to a
constant value.
13

14. Magnetic Flux Density of an Infinite
Line Current Using Ampere’s Law
Consider an infinite line current along the z-
axis carrying current in the +z-direction:
I
14

15. Magnetic Flux Density of an Infinite Line
Current Using Ampere’s Law (Cont’d)
(1) Assume from symmetry and the right-
hand rule the form of the field
H = aφ H φ
ˆ
(2) Construct a family of Amperian paths
circles of radius ρ where
0≤ρ ≤∞
15

16. Magnetic Flux Density of an Infinite Line
Current Using Ampere’s Law (Cont’d)
y
Amperian path
ρ
x
I
I encl = I
16

17. Magnetic Flux Density of an Infinite Line
Current Using Ampere’s Law (Cont’d)
(4) For each Amperian path, evaluate the
integral
C
∫ H ⋅ d l = Hl length
of Amperian
path.
magnitude of H
on Amperian
path.
∫ H ⋅ d l = Hφ 2π ρ
C
17

18. Magnetic Flux Density of an Infinite Line
Current Using Ampere’s Law (Cont’d)
(5) Solve for B on each Amperian path
I encl
H=
l
I
H = aφ
ˆ
2π ρ
18

19. Magnetic Flux Density
The magnetic flux density vector is related to the magnetic
H
field intensity by the following equation
B = µ H,
T (tesla) or Wb/m2
µ
where is the permeability of the medium. Except for
ferromagnetic materials ( such as cobalt, nickel, and iron),
µ
most materials have values of very nearly equal to that for
vacuum, µ o = 4π ⋅ 10 −7
H/m (henry per meter)
The magnetic flux through a given surface S is given by
Ψ = ∫ B ⋅ d s,
S Wb (weber)
19

20. Law of conservation
of magnetic flux
∫
s
B•ds = 0
Law of conservation of
magnetic flux or Gauss’s law
for magnetostatic field

21. ∇•B = 0
∇ × B = µ0 J
∇• J = 0

22. There are no magnetic flow sources, and the
magnetic flux lines always close upon
themselves

23. Forces due to magnetic field
There are three ways in which force due to magnetic fields can
be experienced
1.Due to moving charge particle in a B field
2.On a current element in an external field
3.Between two current elements
23

24. Force on a Moving Charge
• A moving point charge placed in a
magnetic field experiences a force
given by
Fm = qu × B
The force experienced
by the point charge is
v B in the direction into the
Q
paper.
The force is perpendicular to the direction of charge motion,
and is also perpendicular to B .

25. Lorentz’s Force equation
If a point charge is moving in a region where both
electric and magnetic fields exist, then it experiences a
total force given by
Fe = q E Fe + Fm = F
Fm = qu × B
F = q( E + u × B)
Note: Magnetic force is zero for q moving in the
direction of the magnetic field (sin0=0)

26. Magnetic Force on a current element
One can tell if a magneto-static field is present because it
exerts forces on moving charges and on currents. If a
currentIdl B
element is located in a magnetic field , it experiences a
__
force
Id l ⇔ Q u
d= l B
FI ×
d
Idl
This force, acting on current element , is in a direction
perpendicular to the current element and also perpendicular
B B
to . It is largest when and the wire are perpendicular.
26

27. FORCE ON A CURRENT ELEMENT
• The total force exerted on a circuit C
carrying current I that is immersed in a
magnetic flux density B is given by
F = I ∫ dl × B
C
27

28. Force between two current elements
• Experimental facts: F21 F12
– Two parallel wires × ×
carrying current in I1 I2
the same direction
attract.
– Two parallel wires F21 F12
carrying current in × •
the opposite I1 I2
directions repel.
28

29. Force between two current elements
• Experimental facts:
– A short current- F12 = 0
carrying wire × I2
oriented I1
perpendicular to a
long current-
carrying wire
experiences no
force.
29

30. Force between two current elements
• Experimental facts:
– The magnitude of the force is inversely
proportional to the distance squared.
– The magnitude of the force is proportional to
the product of the currents carried by the two
wires.
30

31. Force between two current elements
• The force acting on a current element I2 dl2
by a current element I1 dl1 is given by
µ 0 I 2 d l 2 × ( I1d l 1 × aR12 )
ˆ
d (d F 12 ) =
4π 2
R12
Permeability of free space
µ0 = 4π × 10-7 F/m
31

32. Force between two current elements
• The total force acting on a circuit C2 having
a current I2 by a circuit C1 having current I1
is given by
µ 0 I1 I 2 d l 2 × ( d l 1 × aR12 )
ˆ
F 12 =
4π C2 1 ∫ C∫ R122
32

33. Force between two current elements
• The force on C1 due to C2 is equal in
magnitude but opposite in direction to the
force on C2 due to C1.
F 21 = − F 12
33