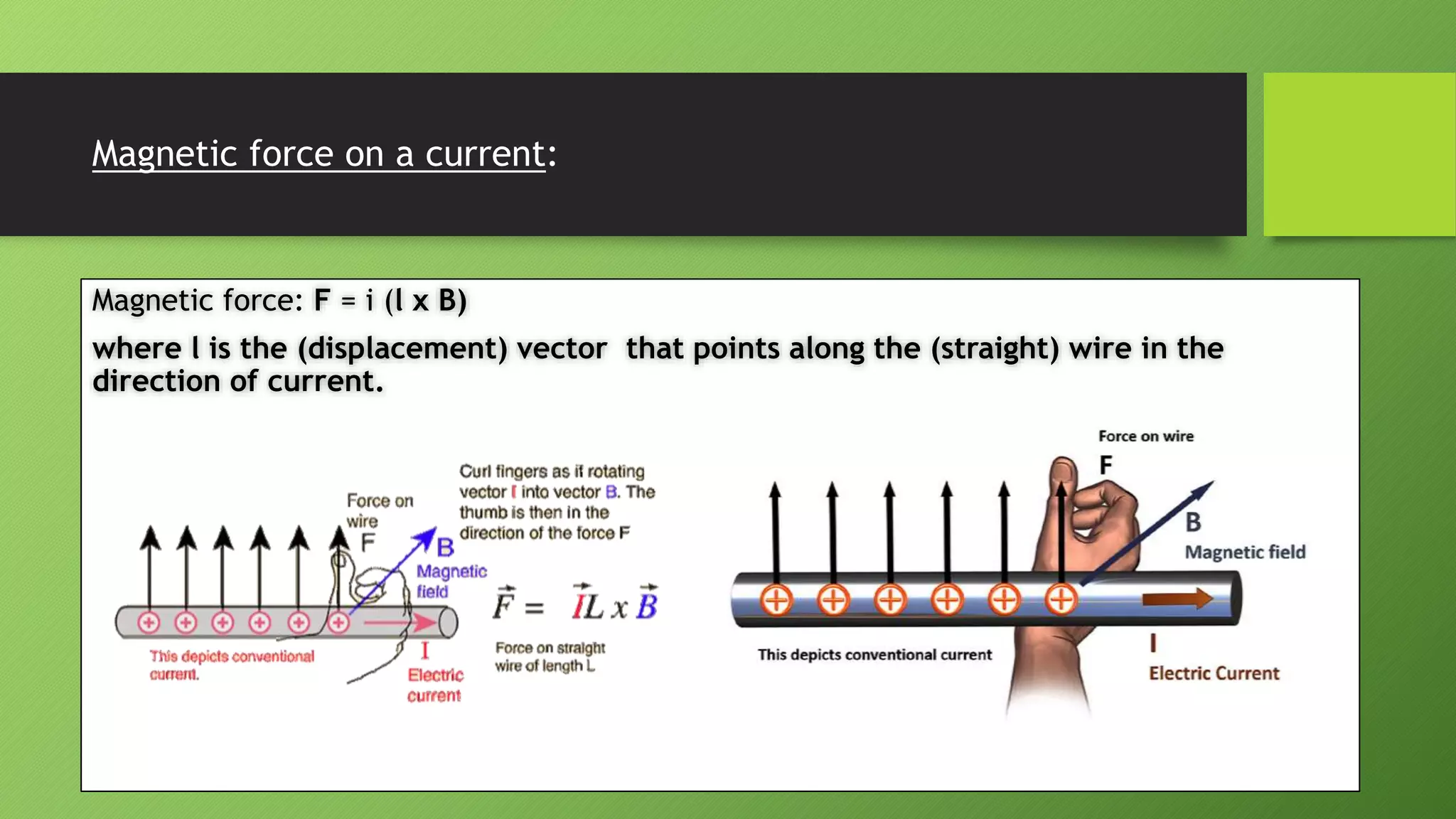
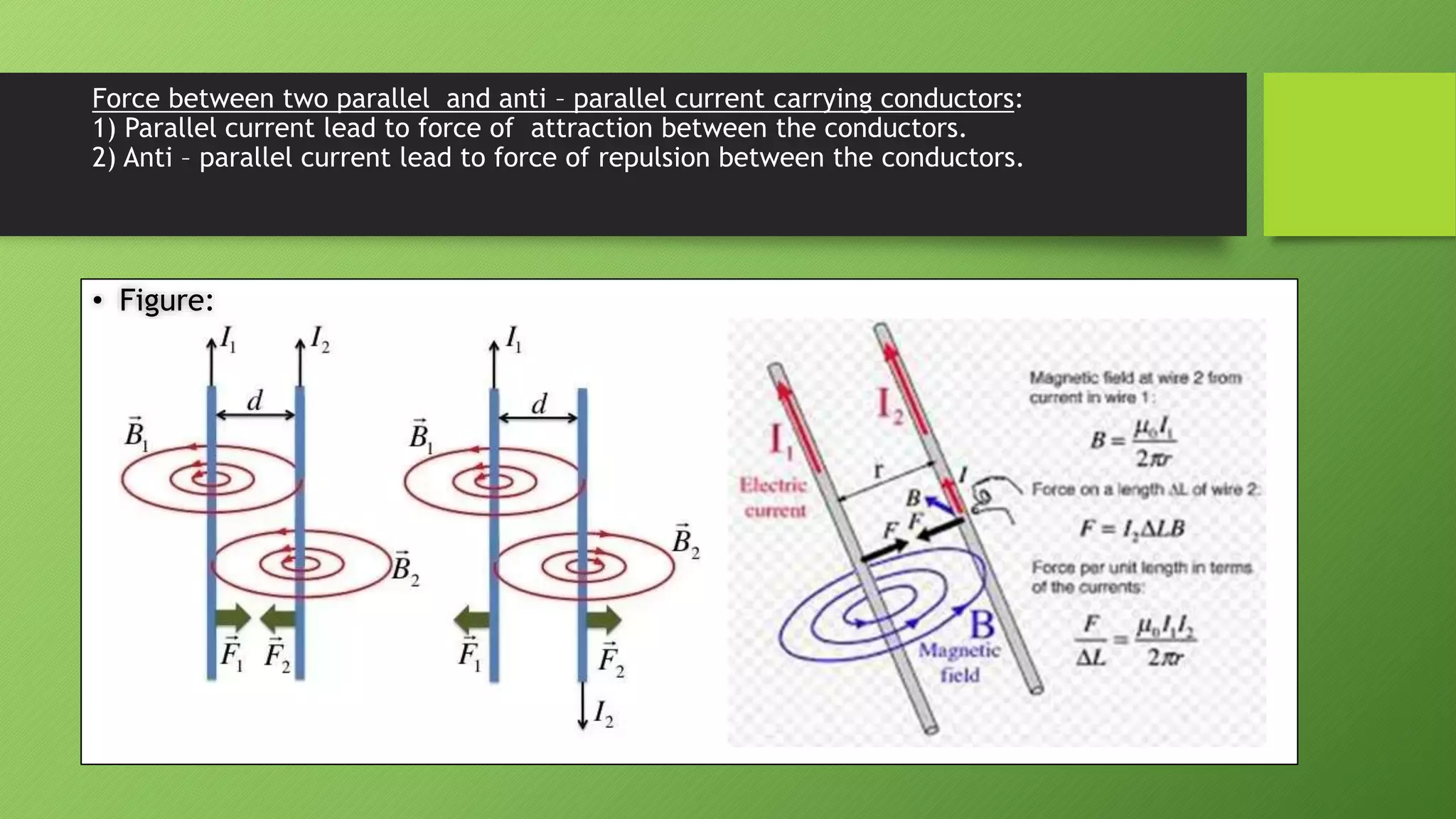
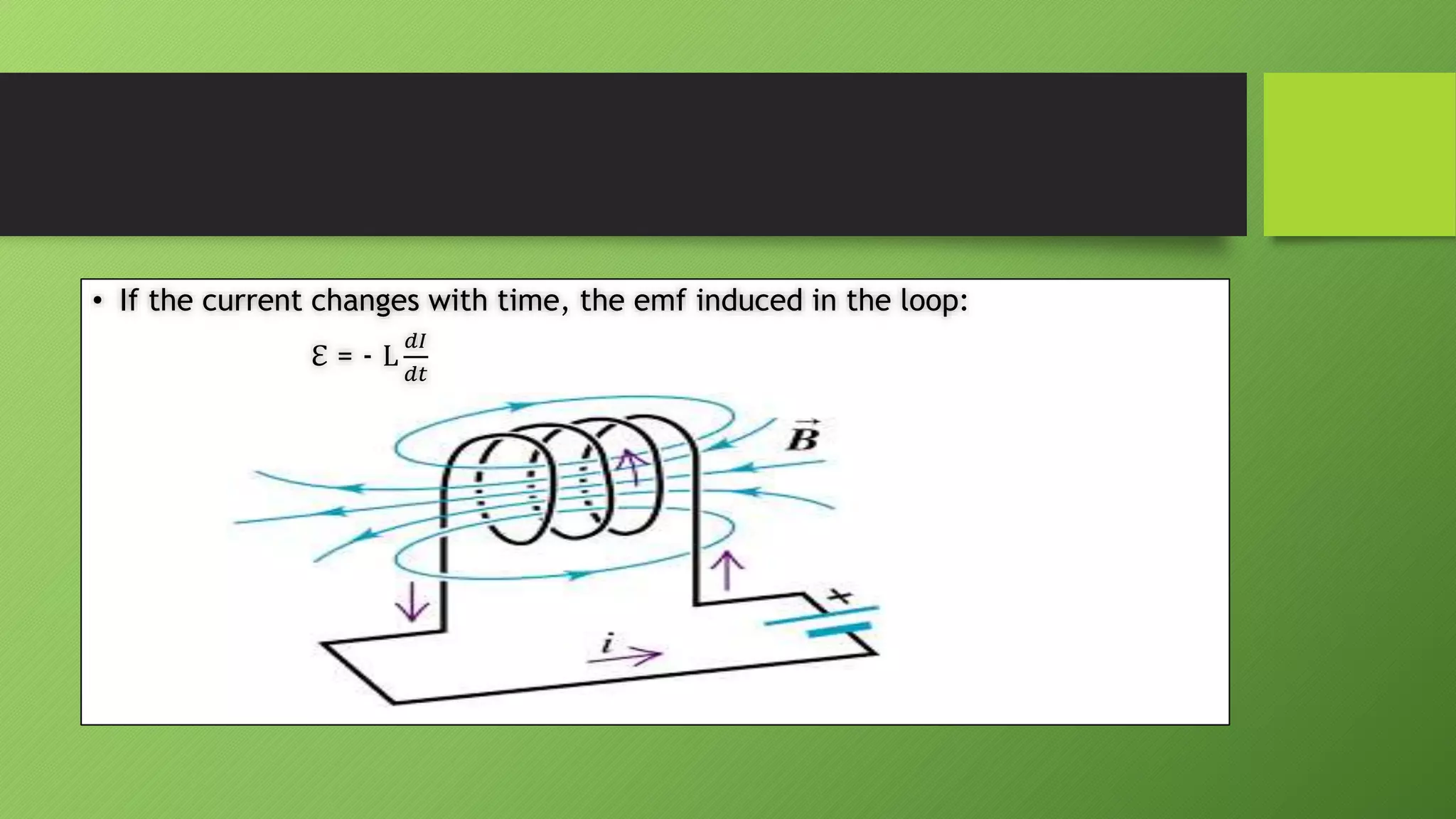
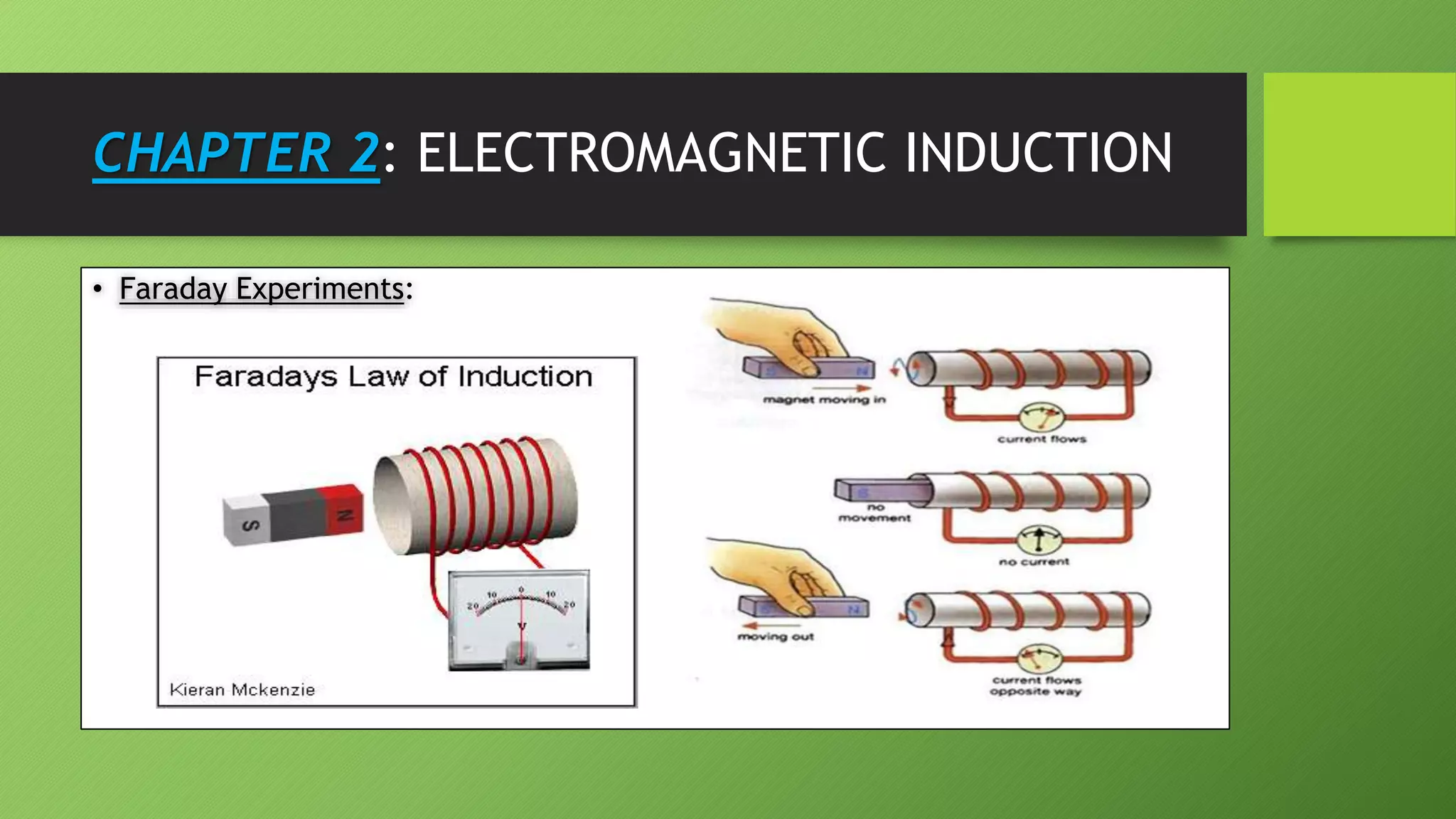
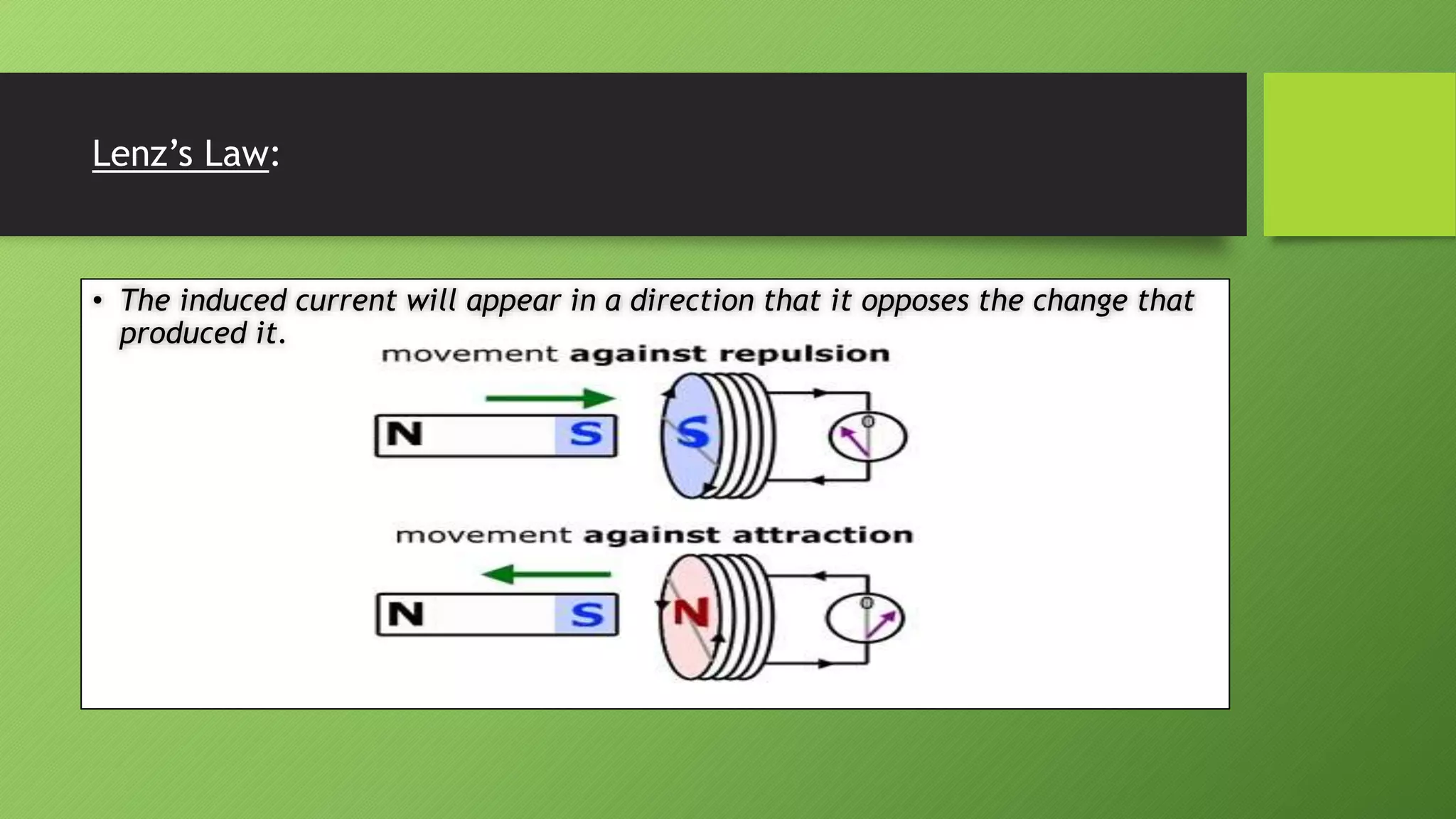
1) A magnetic field is defined as the space around a magnet or current-carrying conductor. Magnetic field lines indicate the direction of the field. 2) Faraday's experiments showed that a changing magnetic field induces an electromotive force (emf) in a nearby circuit. This is known as electromagnetic induction. 3) Lenz's law states that the direction of the induced current will always oppose the change that caused it. This ensures the conservation of energy.

1. UNIT 2

2. CHAPTER 1: Magnetic Field
• Magnetic field:
• Space around a magnet or current carrying conductor. [as the site of magnetic
field].
• Magnetic Induction: Symbol: B

3. • Relation of magnetic field vector to its lines of induction:
• Tangent to a line of induction at any point gives the direction of B at that point.
• Lines of induction are drawn as that the number of lines per unit cross –
sectional area is proportional to the magnetic field vector B.

4. Definition of B:
• Our concern in this chapter:
a) Whether a magnetic field exists at a given point and
b) Action of this field on charges moving through it.
If magnetic field is present in a given space -
The question arises……
1) What is the direction of the magnetic field B as the particle moves in space???
2) What is the direction of force??
3) What is the relation between the velocity of the particle, magnetic field and
the force acting on the particle??

5. • Direction of B:
• Assumption: no electric force and neglecting gravity.
• Consider a positive test charge 𝑞0.
• Test charge fired with arbitrary velocity v through a point.
• If a sideways deflecting force F acts on it, we assert that a
magnetic field is present at that point.
• We define the magnetic induction B of this field in terms of F
and other measured quantities.

6. • Varying the direction of v through the given
point, keeping the magnitude of v unchanged,
we observe:
1) F will always remain at right angles to v.
2) Magnitude of F will change.
• For a particular orientation the force F
becomes zero.
• We define this direction as the direction of the
magnetic field B.

7. • Direction of F:
• Orient the velocity v so that the test charge moves at right angles to B.
• Maximum force acts on the particle.
• Defining B:
• If a positive test charge 𝑞0 is fired with velocity v through a point and if
(sideways) force F acts on the moving charge, a magnetic induction B is present
at that point, where B satisfies the vector relation:
F = 𝑞0 v x B
• Magnitude of the magnetic deflecting force F, according to the rules of vector
products:
F = 𝑞0𝑣𝐵𝑠𝑖𝑛𝜃

8. • F = 𝑞0 v x B , F = 𝑞0𝑣𝐵𝑠𝑖𝑛𝜃
• Above equations show relation among the vectors.
• F is always at right angles to the plane formed by v and B and hence
always a sideways force.
• Consistency of the above equation: Special Case:
A. Case I: Magnetic force vanishes as v → 0.
B. Case II: Magnetic force vanishes if v is either parallel or antiparallel
to the direction of B [𝜃 = 0 or 𝜃 = 180]
C. Case III: If v is at right angles to B [𝜃 = 90] the deflecting force has a
maximum value F = 𝑞0𝑣𝐵

9. Direction of magnetic force for a positive and negative charge:
• Right – hand thumb rule:

10. Magnetic force on a current:
Magnetic force: F = i (l x B)
where l is the (displacement) vector that points along the (straight) wire in the
direction of current.

11. A bubble chamber is a device for rendering visible, by means of small bubbles, the tracks of
charged particles that pass through the chamber. The figure is a photograph taken with such a
chamber immersed in a magnetic induction B and exposed to radiations from large cyclotron –
like accelerator. The curved path is formed by a positive and a negative electron.

12. • If we consider differential element of a conductor of length dl, the force acting
on it can be found by integrating:
dF = i (dl x B)

13. • Sources of magnetic field:
Direction of B can be determined by Right hand thumb rule:
• Figure

14. A current carrying conductor:
Direction of magnetic field can be found using Right hand thumb
rule.

15. A simple Demonstration:
(Direction of magnetic field for current in two directions)

16. Force between two parallel and anti – parallel current carrying conductors:
1) Parallel current lead to force of attraction between the conductors.
2) Anti – parallel current lead to force of repulsion between the conductors.
• Figure:

17. Biot – Savart Law:
• Procedure to compute magnetic field at a point P
due to an arbitrary current distribution:
1) Divide the current distribution into current
elements.
2) Using Biot – Savart law, we calculate the field
contribution dB due to each current element at the
point n question.
3) We find B at that point by integrating the field
contributions for the entire distribution:

18. • Let P be the point at which we want to know the magnetic induction dB associated
with the current element.
• According to Biot – Savart law, dB is given in magnitude:
dB =
𝜇0𝑖
4𝜋
𝑑𝑙 𝑠𝑖𝑛𝜃
𝑟2

19. Application of Biot – Savart Law:
Example: Magnetic Field due to a straight wire carrying current

20. Example :Magnetic Field due to circular current loop:
• Figure

21. CHAPTER 2: ELECTROMAGNETIC INDUCTION
• Faraday Experiments:

22. • Faraday’s Experiment:

23. Faraday’s Law:
• Experiment shows that there will be an induced emf in the right coil whenever
the current in the left coil is changing.
• It is the rate at which the current is changing and not the size of the current
that is significant.
• According to Faraday:
• The change in the flux 𝜑𝐵 of the magnetic induction for the right coil is an
important factor.
• Flux may be set up by a bar magnet or a current loop.

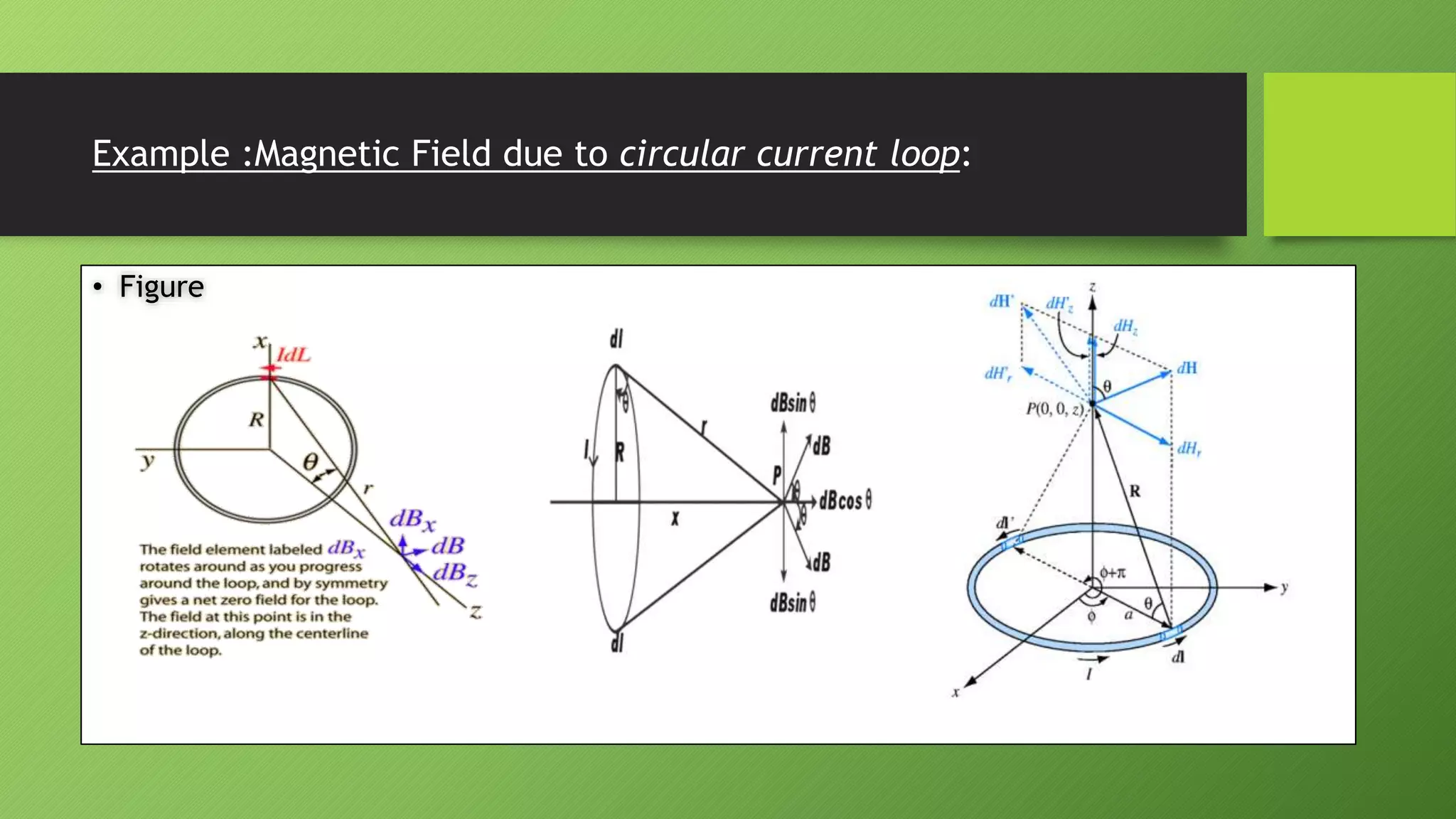
24. • Faraday’s law of induction says that the induced emf ℇ in a circuit is equal to
the negative rate at which the flux through the circuit is changing given by:
ℇ = -
𝑑𝜑𝐵
𝑑𝑡
------[Faraday’s law of induction] -----(1)

25. • Equation [1] applied to a coil to N turns, an emf appears in every turn.
• Emfs needs to be added.
• If the coil is tightly wound that each turn can be occupies the same region of space, the flux
through each turn will be the same.
• The induced emf is given by:
ℇ = - N
𝑑𝜑𝐵
𝑑𝑡
= −
𝑑𝑁𝜑𝐵
𝑑𝑡
where 𝑁𝜑𝐵 is called the flux – linkages in the device.

26. Faraday’s Experiment:
Experiment 1: Pulling the loop of wire to the right through a magnetic field produces a
current in the loop.
Experiment 2: Pulling the magnet to the left holding the loop of wire stationary leads to
flow of current in the loop.
Experiment 3: Both magnet and loop are held at rest. Changing the strength of the
magnetic field leads to flow of current in the loop.

27. • A changing magnetic field induces an electric field.
ℇ = 𝐸. 𝑑𝑙 = -
𝑑𝜑𝐵
𝑑𝑡
• E is related to the change in B by equation:
𝐸. 𝑑𝑙 = -
𝜕𝐵
𝜕𝑡
. 𝑑𝑎 ---- [Faraday’s law in integral form]
• We can convert it to differential form by applying Stokes’ theorem:
∇ 𝑋 𝐸 = -
𝜕𝐵
𝜕𝑡

28. Lenz’s Law:
• The induced current will appear in a direction that it opposes the change that
produced it.

29. INDUCTANCE (SELF AND MUTUAL):
• Consider:
• Two loops of wire at rest.
• Steady current 𝐼1 around loop 1 produces a magnetic field 𝐵1.
• Some fields of lines pass through loop 2.
• 𝜑2 be the flux of 𝐵1through loop 2.
• By Biot – Savart Law:
𝐵1 =
𝜇0𝐼1
4𝜋
𝑑𝐼1 × 𝓇
𝓇2
• Flux through loop 2:
𝜑2 = 𝐵1. 𝑑𝑎2

30. • Example:

31. • Example:

32. • 𝐵1 is proportional to the current 𝐼1.
Flux:
𝜑2 = 𝑀21 𝐼1
where 𝑀21 = constant of proportionality; known as the mutual inductance of the
two loops.

33. • Expression for mutual inductance:
𝑀21 =
𝜇0
4𝜋
𝑑𝐼1.𝑑𝐼2
𝓇
Two Important things about mutual inductance:
1) 𝑀21 is a purely geometrical quantity, having to do with the sizes, shapes, and
relative positions of the two loops.
2) Integral in equation is unchanged if we switch the roles of loop 1 and loop 2,
𝑀21= 𝑀12

34. SELF – INDUCTANCE:
• Changing current not only induces emf in ant nearby loops, it also induces an
emf in the source loop itself.
• Magnetic field (or flux) is proportional to the current:
Φ = 𝐿𝐼
• NOTE:
Constant of proportionality L is called the self – inductance of the loop.
Depends on the geometry (size and shape) of the loop.

35. • If the current changes with time, the emf induced in the loop:
ℇ = - L
𝑑𝐼
𝑑𝑡

36. • Figure:

37. Energy stored in a magnetic field:
• Energy stored in a magnetic field:
• Takes certain amount of energy to start current flowing in
a circuit.
• Work must be done against the back emf to initiate current
in the circuit.
• Work done on a unit charge, against the back emf, in one
trip around the circuit is -ℇ. (minus sign records the fact
that this work done by the agent against the emf)
• The amount of current per unit time passing down the wire
is I.

38. • Total work done per unit time:
dW/dt = -ℇI = (LI)dI/dt
• If we start with zero current and build to a final value I, the work done (on
integrating over the last equation):
W = ½ 𝐿𝐼2
.
• Alternate expression for energy stored in a magnetic field:
W =
1
2𝜇0
𝐵2𝑑𝜏
• In view of this result, we say the energy is “stored in the magnetic field”, in the
amount
𝐵2
2𝜇0
per unit volume.

39. 1)Current loop as a magnetic dipole and its magnetic moment.
2)Torque on a current loop.
• Figure shows a rectangular loop of length a and b placed in
a uniform magnetic field.
• Sides 2 and 4 are always normal to the direction of the
magnetic field.
• Normal 𝑛𝑛′ to the plane makes an angle 𝜃 with the
direction of B.

40. • Force acting on the loop carrying current:
• Net force on the loop is the resultant of the forces on the
four sides of the loop.
• On side 1 the vector l points in the direction of current and
has magnitude a.
• The angle between l and B is 90 - 𝜃.
• Magnitude of force on this side:
𝐹1 = iaB sin (90 - 𝜃) = iaB cos 𝜃.
• From F = i (l x B), the direction of 𝐹1 is out of the plane.
• Force 𝐹1 and 𝐹3 have same magnitude but are pointing in
opposite direction.

41. • Force 𝐹1 and 𝐹3 do not produce any torque as the line of action of force are
along the same line.
• Magnitude of force 𝐹2 and 𝐹4 = ibB sin 𝜃.
• Line of action of does not coincide, net torque acts on the loop.
• Magnitude of 𝜏 can be found by calculating the torque caused by 𝐹2 about the
axis n and doubling it, for 𝐹4 exerts the same torque about the same axis.
𝜏 = 2 𝑖𝑏𝐵
𝑎
2
𝑠𝑖𝑛𝜃
• This torque acts on every coil. If there are N turns, the torque on the entire coil
–
𝜏 = 𝑁𝑖𝑎𝑏𝐵 𝑠𝑖𝑛𝜃 = 𝑁𝑖𝐴𝐵 𝑠𝑖𝑛𝜃 (where 𝐴 is area of the coil)
• Above equation holds for all plane loops of area A, whether they are rectangular
or not

42. Figure: Direction of force acting on a current carrying loop placed in a uniform
magnetic field.

43. • A current loop orienting itself in an external magnetic field reminds us of action
of a compass needle in such a field.
• One face of the loop behaves as a north pole; other face behaves like a south
pole.
• Compass needles, bar magnets and current loops can all be regarded as
magnetic dipoles.

44. • Definition of a dipole:
• A structure is called an electric dipole if –
a) When placed in an external electric field it experiences a torque given by:
𝜏 = 𝑝 𝑋 𝐸 (where p is the electric dipole moment)
b) It sets up a field of its own at distant point (described qualitatively by lines of
forces)

45. • Magnitude of the torque –
𝜏 = 𝑝𝐸𝑠𝑖𝑛𝜃 (𝜃 is the angle between p and E)
• Comparing equation 𝜏 = 𝑁𝑖𝐴𝐵 𝑠𝑖𝑛𝜃 with the expression for torque (𝜏 = 𝑝𝐸𝑠𝑖𝑛𝜃)
• Comparison suggests that NiA can be taken as the magnetic dipole moment 𝜇 –
𝜇 = NiA

46. • We can write the torque on a current loop in vector form as –
𝝉 = 𝝁 𝑿 𝑩

47. Direction of the magnetic dipole moment:
• Magnetic dipole moment of the loop must be
taken along the axis of the loop.
• Direction:
• Let the fingers of the right hand curl around
the loop in the direction of the current.
• The extended right thumb will then point in
the direction of 𝜇.

48. Magnetic Dipole Moment: