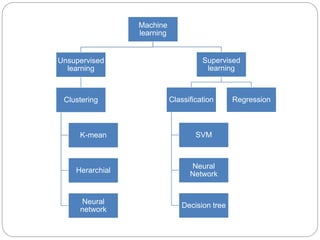
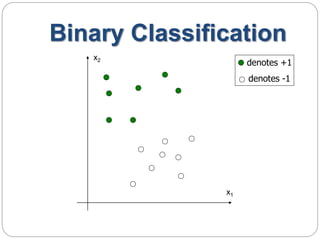
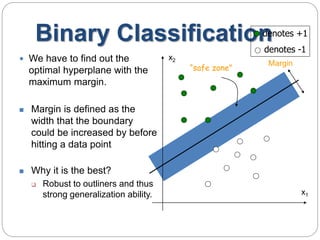
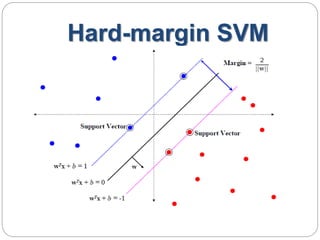
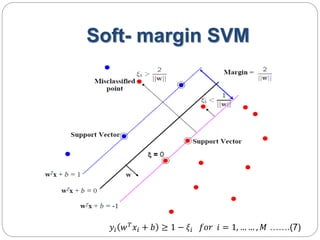
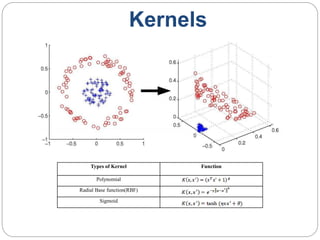
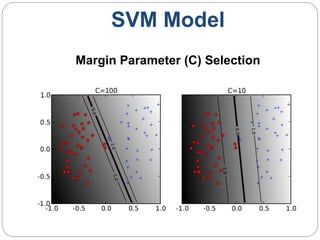
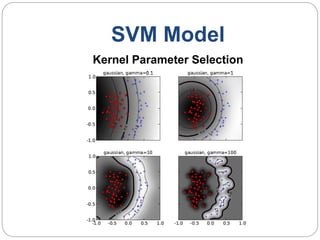
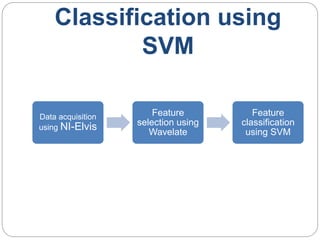
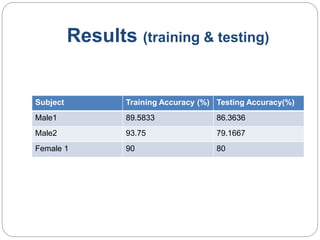
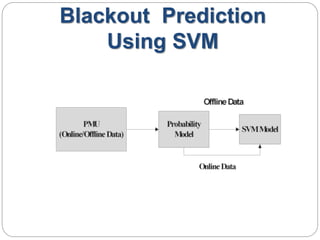
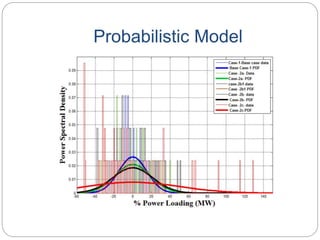
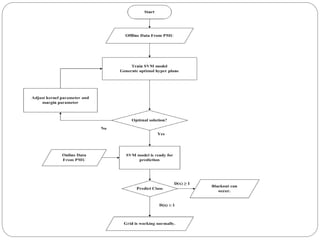
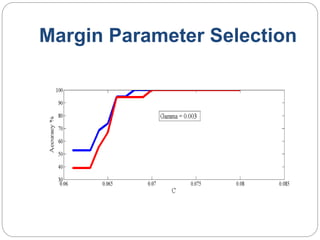
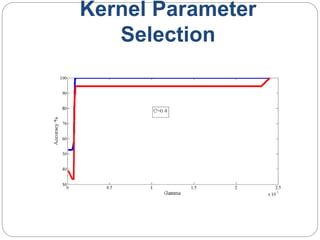
This document provides an overview of event classification and prediction using support vector machines (SVM). It begins with an introduction to classification, machine learning, and SVM. It then discusses binary classification with SVM, including hard-margin and soft-margin SVM, kernels, and multiclass classification. The document presents case studies on classifying hand movements from electromyography data and predicting power grid blackouts using SVM. It concludes that SVM is effective for these classification tasks and can initiate prevention mechanisms for predicted events.

1. By
Ruta Ashok Kambli
(122071013)
Event Classification & Prediction Using
Support Vector Machine

2. Scope of Presentation
 Introduction
 Support Vector Machine(SVM)
 Hard-margin SVM
 Soft -margin SVM
 Kernels
 Multiclass classification
 SVM Model Selection
 Case Studies & Results
 Conclusion

3. Introduction
 Classification & Prediction
 Machine Learning
 Support Vector Machine

4. Machine
learning
Unsupervised
learning
Clustering
K-mean
Herarchial
Neural
network
Supervised
learning
Classification
SVM
Neural
Network
Decision tree
Regression

5. Support Vector
Machines
• Supervised machine learning model.
• Analyse data and recognize patterns.
• Used for classification and regression
analysis.

6. Binary Classification
Consider training data set (𝑥𝑖, 𝑦𝑖) for (i = 1, . . . , M),
with 𝑥𝑖 ∈ ℝ 𝑑
and 𝑦𝑖 ∈ {−1, 1}, learn a classifier
D(x) such that,
𝐷(𝑥𝑖)
≥ 1, 𝑓𝑜𝑟 𝑦𝑖 = 1
≤ −1, 𝑓𝑜𝑟 𝑦𝑖 = −1
……(1)
ie. 𝑦𝑖 𝐷 𝑥𝑖 ≥ 1 for a correct classification.

7. Binary Classification
x1
x2
denotes +1
denotes -1

8.  How would you classify these
points using a linear
discriminant function in order
to minimize the error rate?
Binary Classificationdenotes +1
denotes -1
x1
x2
 Infinite number of answers!

9.  How would you classify these
points using a linear
discriminant function in order
to minimize the error rate?
Binary Classificationdenotes +1
denotes -1
x1
x2
 Infinite number of answers!

10.  How would you classify these
points using a linear
discriminant function in order
to minimize the error rate?
Binary Classificationdenotes +1
denotes -1
x1
x2
 Infinite number of answers!

11. x1
x2 How would you classify these
points using a linear
discriminant function in order
to minimize the error rate?
Binary Classificationdenotes +1
denotes -1
 Infinite number of answers!
 Which one is the best?

12. Binary Classification
“safe zone”
 We have to find out the
optimal hyperplane with the
maximum margin.
 Margin is defined as the
width that the boundary
could be increased by before
hitting a data point
 Why it is the best?
 Robust to outliners and thus
strong generalization ability.
Margin
x1
x2
denotes +1
denotes -1

13. Hard-margin SVM

14. Minimise : 𝑄 𝑤, 𝑏 =
1
2
𝑤 2
…….(2)
Subject to: 𝑦𝑖 𝑤 𝑇 𝑥𝑖 + 𝑏 ≥ 1 𝑓𝑜𝑟 𝑖 = (1, … … , 𝑀)
…….(3)
Q(w, b,𝛼)=𝑊 𝑇
𝑊 − 𝑖=1
𝑀
𝛼𝑖 𝑦𝑖 𝑤 𝑇
𝑥𝑖 + 𝑏 − 1 ……(4)
Where 𝛼 = (𝛼𝑖, … … 𝛼 𝑀) and 𝛼𝑖 are the nonnegative Lagrange
multipliers.
• The optimal solution of (4) is given by the saddle
point.
• Where (4) is minimized with respect to w
• Maximized with respect to 𝛼𝑖 (≥ 0)
• Maximized or minimized with respect to b
according to the sign 𝑖=1
𝑀
𝛼𝑖 𝑦𝑖

15. Soft- margin SVM
𝑦𝑖 𝑤 𝑇
𝑥𝑖 + 𝑏 ≥ 1 − 𝜉𝑖 𝑓𝑜𝑟 𝑖 = 1, … … , 𝑀 …….(7)

16. Soft margin SVM
𝑚𝑖𝑛𝑖𝑚𝑖𝑠𝑒 𝑄 𝑤, 𝑏, 𝜉 =
1
2
𝑤 2
+
𝐶
𝑃 𝑖=1
𝑀
𝜉𝑖
𝑃
……..(5)
𝑆𝑢𝑏𝑗𝑒𝑐𝑡 𝑡𝑜 𝑦𝑖 𝑤 𝑇 𝑥𝑖 + 𝑏 ≥ 1 − 𝜉𝑖 𝑓𝑜𝑟 𝑖 = 1, … … , 𝑀 ….(6)
𝑄 𝑤, 𝑏, 𝛼, 𝛽
=
1
2
𝑤 2 + 𝐶
𝑖=1
𝑀
𝜉𝑖 −
𝑖=1
𝑀
𝛼𝑖 𝑦𝑖 𝑤 𝑇 𝑥𝑖 + 𝑏 − 1 + 𝜉𝑖 −
𝑖=1
𝑀
𝛽𝑖 𝜉𝑖
……(7)

17. Kernels
Types of Kernel Function
Polynomial
Radial Base function(RBF)
Sigmoid

18. Multiclass Classification
 Initially SVM is Binary Classifier.
 Most of the practical applications involve
multiclass classification.
 One against One Approach.
 If n is the number of classes, we generate
n(n-1)/2 models.
 It is not practical for large-scale linear
classification.

19. SVM Model
Margin Parameter (C) Selection

20. SVM Model
Kernel Parameter Selection

21. K-fold Cross Validation
 Create a K-fold partition of the dataset.
 For each of K experiments, use K-1 folds for training
and the remaining one for testing.
 The advantage of K-Fold Cross validation is that all
the examples in the dataset are eventually used for
both training and testing

22. Classification using
SVM
Data acquisition
using NI-Elvis
Feature
selection using
Wavelate
Feature
classification
using SVM

23. Data acquisition using NI-Elvis
 Two connectors are
connected to Flexor
Digitorum supercialis
(FDS) muscle.
 The readings are
taken for different
hand movements.

24. Data acquisition using NI-Elvis
This is time verses
amplitude graph of hand
movement data.
 Class 1 :open hand
 Class 2 : closed hand
 Class 3 :wrist flexion

26. Results (training & testing)
Subject Training Accuracy (%) Testing Accuracy(%)
Male1 89.5833 86.3636
Male2 93.75 79.1667
Female 1 90 80

27. Blackout Prediction
Using SVM

28. Probabilistic Model

30. Kernel Selection
Kernel Training Accuracy % Testing Accuracy%
Polynomial 100 94.44
Radial 100 100
Sigmoid 52.63 38.89

31. Margin Parameter Selection

32. Kernel Parameter
Selection

33. Conclusion
 Results of first case study show that, single
channel surface Electromyogram analysis is
simple, less expensive and effective.
 The second case study shows, using blackout
prediction model we can predict blackout before it
occurs.
 Here output of SVM is given to emergency control
system, which initiates the prevention mechanism
against the blackout.

34. Refferences
1. “Support Vector Machines for Pattern
Classification” by Shigeo Abe
2. “Classification of low-level finger contraction
from single channel Surface EMG” by Vijay Pal
Singh and Dinesh Kant Kumar
3. “Fault Location in Power Distribution System
with Distributed Generation Using Support
Vector Machine,” by Agrawal, R.Thukaram
4. M. R. Ahsan, M. I. Ibrahimy, and O. O. Khalifa,
“EMG signal classication for human computer
interaction: A review,"European Journal of
Scientic Research, vol. 33, no. 3, pp. 480-501,
2009.

35. References
5. J. Kim, S. Mastnik, and E. Andr,”EMG-based
hand gesture recognition for realtime biosignal
interfacing,"13th international conference on
Intelligent user interfaces, 2008, pp.3039.
6. K. Englehart and B. Hudgins, “A robust, real-
time control scheme for multifunction
myoelectric control,"Biomedical Engineering,
IEEE Transactions on, vol. 50, no. 7, pp.
848854, 2003.
7. C Rudin, D Waltz, and R N Anderson, “Machine
learning for the new york city power grid,"IEEE
Trans. on Pattern analysis and machine
intelligence , VOL. 34, NO. 2, February 2011

36. THANK YOU