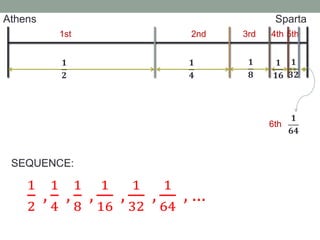
This document defines geometric series and provides formulas to calculate the sum of finite and infinite geometric series. It also provides examples of problems involving geometric series, such as calculating sums, determining convergence, and applying geometric series to real-world scenarios like compound interest, population growth, and bouncing balls.

1. GEOMETRIC SERIES
Mr. Jhon Paul A. Lagumbay
Mathematics Teacher

2. Definition:
A geometric series is the sum of the
terms of a geometric sequence. If the
number of terms in the geometric sequence
is finite, the sum of terms is called a finite
geometric series. If not, the series is
infinite.

3. The sum of the first n terms in a geometric
sequence is given by
𝑆 𝑛 =
𝑎1 1 − 𝑟 𝑛
1 − 𝑟
, 𝑟 ≠ 1
where
𝑆 𝑛 = the sum of the first n terms
𝑎1 = the first term,
𝑟 = the common ratio, and
𝑛 = the number of terms.

4. Problem 1
1. Find the sum of the first seven terms of the
geometric sequence -5, 10, -20, 40, …
2. Find the sum of the first six terms of the
geometric sequence 2, -8, 32, -128, …

5. Problem 2
Angelo and his employer agreed that he
will be paid based on the following scheme: 1
peso on the first day, 2 pesos on the second
day, 4 pesos on the third day, 8 pesos on the
fourth day, and so on. How much would
Angelo receive after working for 15 days with
no absences?

6. Problem 3
A bacteria culture started out with 500
bacteria and doubles in number every hour.
How many bacteria will be reproduced after 12
hours?

7. Problem 4
Mike deposited Php 850 into the bank in
July. From July to December, the amount of
money which he deposited into the bank
increased by 25% per month. What is the total
amount of money in his account after
December?

8. Problem 5
A ball tossed to a height of 4 meters
rebounds to 40% of its previous height. Find
the distance the ball has traveled when it
strikes the ground for the fifth time.

9. Problem 6
A contract specifies that Marlyn Figueroa
will receive a 5% pay increase each year for the
next 30 years. She is paid Php 120,000.00 the
first year. What is her total lifetime salary over
a 30-year period?

10. Review Problem
Suppose you save 1 peso on the first day
of a month, 2 pesos on the second day, 4
pesos on the third day, and so on. That is, each
day you save twice as much as you did the day
before.
a. What will you put aside for saving on the
15th day of the month?
b. How much will you saved in all on the 30th
day of the month?

11. EXPLORE!!!
PARADOX OF ZERO
Here’s a paradox devised by Zeno 2500 years ago:
To go from Athens to Sparta, first you must travel
half the distance. Then, you must again travel half of the
remaining distance each time. Will you ever reach Sparta?

12. Athens Sparta
1st 2nd 3rd 4th 5th
𝟏
𝟐
𝟏
𝟒
𝟏
𝟖
𝟏
𝟏𝟔
𝟏
𝟑𝟐
𝟏
𝟔𝟒
6th
1
2
,
1
4
,
1
8
,
1
16
,
1
32
,
1
64
, …
SEQUENCE:

13. Infinite Geometric Series
If −1 < 𝑟 < 1, then the infinite geometric series
𝑎1 + 𝑎1 𝑟 + 𝑎1 𝑟2
+ 𝑎1 𝑟3
+ ⋯ + 𝑎1 𝑟 𝑛−1
+ ⋯
converges into a particular value.
Then, the sum of an infinite geometric
series is given by:
𝑆∞ =
𝑎1
1 − 𝑟
, where 𝑟 < 1
The series converges because each term gets
smaller and smaller (since −1 < 𝑟 < 1).

14. Problem 7
1. Find the sum of the infinite geometric
series
1
2
+
1
4
+
1
8
+ ⋯
2. Find the sum of this infinite geometric
series
1
3
+
1
9
+
1
27
+ ⋯

15. Problem 8
Determine whether each geometric series
converges. If so, find the sum of each geometric
series.
1. 1 +
1
10
+
1
100
+
1
1000
+ ⋯
2. 8 − 4 + 2 − 1 + ⋯
3. 2 + 4 + 8 + 16 + ⋯
4. 3 + 9 + 27 + 81 + ⋯
5. −
2
3
+
2
9
−
2
27
+
2
81
+ ⋯
6. 36 + 6 + 1 +
1
6
+ ⋯

16. Problem 9
1. Show that the repeating decimals 0. 6
equals
2
3
.
2. Show that the repeating decimals 0. 7
equals
7
9
.

17. Problem 10
A ball tossed to a height of 4 meters
rebounds to 40% of its previous height. Find
the total distance travelled by the ball by the
time it comes to rest.