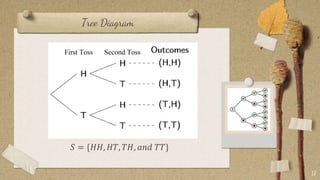
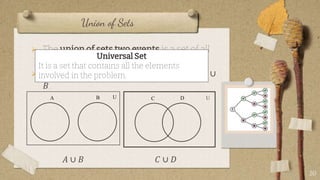
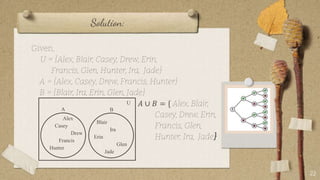
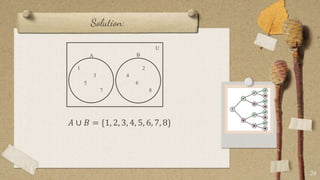
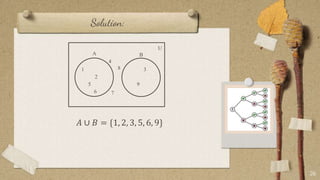
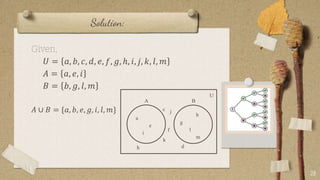
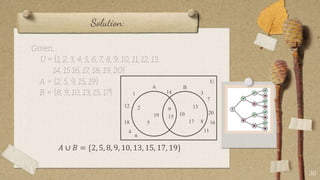
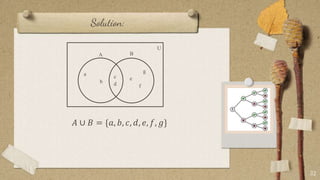
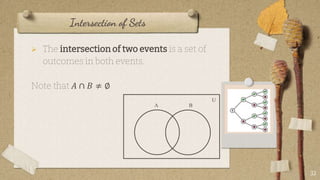
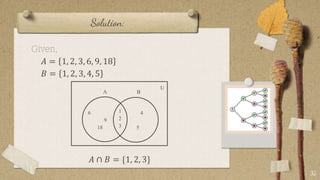
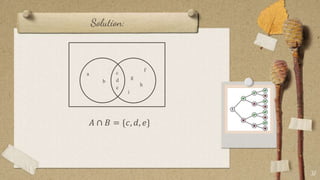
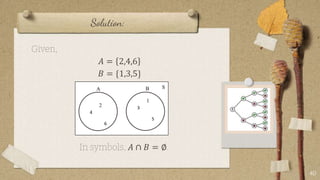
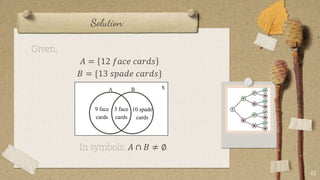
The document contains classroom rules established by Queen Melvs for her students. It lists 7 rules including being on time, actively participating, raising your hand to speak, showing respect, avoiding noise, using appropriate language, and doing your best. It also describes an activity called "The Boat is Sinking" which divides students into groups and tasks them with arranging themselves according to different criteria like favorite sport or food. It provides examples to illustrate set theory concepts like the sample space, events, union, intersection, and Venn diagrams. It asks students to think of a word problem applying these concepts and present it in class.

1. Queen Melvs’ Rule
Classroom Rules

2. Queen Melvs’ Rule:
1. Be on time in class. I
want you to be here
inside the classroom
before the discussion
started.
2.Be active in class. I want
everyone to participate
during our discussions.
2

3. 3.Raise your hand if you
want to ask something to
clarify or ask permission.
4.Respect everyone in the
class.
5.Avoid unnecessary noise
to make sure that
everyone can listen and
pay attention to our
lesson.
3

4. 6.Keep your language clean
and appropriate for the
classroom setting
7. And lastly, do your best.
I want you to put effort
into understanding our
lessons.
4

5. The Boat is Sinking
Activity:

6. Mechanics of the Game:
1. The class will be divided
into 4 groups.
2.The participants are
given the premise that
the imaginary boat they
are on is sinking and
therefore have to form
groups to make it to
safety.
6

7. 3.The facilitator (teacher)
starts by saying “The boat
is sinking group
yourselves into ...” he/she
group also assigns
depending on the given
details the group has to
form and lined up.
7

8. 4.Once everyone has formed
their group, the group will
sit and shout their yell.
5.Once everyone has formed
their group the
facilitators make sure to
check if no one is out of
place. If there was then
that group will not get a
point.
8

9. 6.The first group who
finishes the task will
gain 4 points, the second
3 points, the third 2
points, and the last group
will gain 1 point.
7. The group that gets the
highest points will be the
winner.
9

10. 1. The boat is sinking
arrange yourselves
according to your favorite
sport in alphabetical order.
10

11. 11
2. The boat is sinking
arrange yourselves
according to your favorite
food in alphabetical order.

12. 12
3. The boat is sinking
arrange yourselves
according to your birth
date in order.

13. 13
4. The boat is sinking
arrange yourselves
according to your crush's
name in alphabetical
order.

14. 14
5. The boat is sinking
arrange yourselves
according to your favorite
country in alphabetical
order.

15. Events, Union,
and Intersection
Prepared by: Melvin Verdadero

16. Sample Space
Sample space is a set of all outcomes of an
experiment.
𝑆 = 𝐻𝑒𝑎𝑑, 𝑇𝑎𝑖𝑙
16

17. Tree Diagram
𝑆 = {𝐻𝐻, 𝐻𝑇, 𝑇𝐻, 𝑎𝑛𝑑 𝑇𝑇}
17
First Toss Second Toss

18. Event
 Is a subset of the sample space.
 It may contain some, all, or none of the
possible outcomes comprising the sample
space.
 It may be a simple event or a compound
event.
18

19. Event
19
Simple Event
 It consists of a
single outcome or
a single event that
cannot be further
broken down into
smaller events
Compound Event
 Is any event
combining two or
more simple
events.

20. Union of Sets
 The union of sets two events is a set of all
outcomes in both events.
 The union of sets A and B is denoted by 𝐴 ∪
𝐵.
𝐴 ∪ 𝐵 𝐶 ∪ 𝐷
20
U U
B
A C D
Universal Set
It is a set that contains all the elements
involved in the problem.

21. Example 1:
Ten best friends Alex, Blair, Casey, Drew, Erin,
Francis, Glen, Hunter, Ira, and Jade play
different sports. Let A play soccer which are
Alex, Casey, Drew, Francis, and Hunter. And
let B play tennis which are Blair, Ira, Erin,
Glen, and Jade. Find 𝐴 ∪ 𝐵 and draw a Venn
diagram to illustrate 𝐴 ∪ 𝐵.
21

22. Solution:
Given,
U = {Alex, Blair, Casey, Drew, Erin,
Francis, Glen, Hunter, Ira, Jade}
A = {Alex, Casey, Drew, Francis, Hunter}
B = {Blair, Ira, Erin, Glen, Jade}
𝐴 ∪ 𝐵 = { Alex, Blair,
Casey, Drew, Erin,
Francis, Glen,
Hunter, Ira, Jade}
22
Blair
Ira
Erin
Glen
Jade
Alex
Casey
Drew
Francis
Hunter
U
B
A

23. Example 2:
Given,
𝑈 = 1, 2, 3, 4, 5, 6, 7, 8, 9,
𝐴 = 1, 3, 5, 7
𝐵 = 2, 4, 6, 8
Find 𝐴 ∪ 𝐵 and draw a Venn diagram.
23

24. Solution:
𝐴 ∪ 𝐵 = {1, 2, 3, 4, 5, 6, 7, 8}
24
1
3
5
7
2
4
6
8
U
B
A

25. Example 3:
Draw a Venn diagram to represent the
following:
𝑈 = 1, 2, 3, 4, 5, 6, 7, 8, 9
𝐴 = 1, 2, 5, 6
𝐵 = 3, 9
25

26. Solution:
𝐴 ∪ 𝐵 = {1, 2, 3, 5, 6, 9}
26
1
2
5
6
3
9
U
B
A
4
8
7

27. Example 4:
Draw a Venn diagram to represent the first
half of the English alphabet. Let A be the
vowels and let B be the letters b, g, l, and m.
27

28. Solution:
Given,
𝑈 = 𝑎, 𝑏, 𝑐, 𝑑, 𝑒, 𝑓, 𝑔, ℎ, 𝑖, 𝑗, 𝑘, 𝑙, 𝑚
𝐴 = 𝑎, 𝑒, 𝑖
𝐵 = 𝑏, 𝑔, 𝑙, 𝑚
𝐴 ∪ 𝐵 = {𝑎, 𝑏, 𝑒, 𝑔, 𝑖, 𝑙, 𝑚}
28
a
e
i
b
g
l
m
U
A B
c j
k
d
f
h

29. Example 5:
Let U be a universal set consisting of all the
natural numbers until 20 and set A and B be a
subset of U defined as 𝐴 = {2, 5, 9, 15, 19} and
𝐵 = {8, 9, 10. 13, 15, 17}.
29

30. Solution:
Given,
U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13,
14, 15 16, 17, 18, 19, 20}
A = {2, 5, 9, 15, 19}
B = {8, 9, 10, 13, 15, 17}
𝐴 ∪ 𝐵 = {2, 5, 8, 9, 10, 13, 15, 17, 19}
30
13
10
17 8
2
19
5
9
15
U
A B
1 3
4
6
7
11
12
14
16
18
20

31. Example 6:
Given,
𝑈 = 𝑎, 𝑏, 𝑐, 𝑑, 𝑒, 𝑓, 𝑔
𝐴 = 𝑎, 𝑏, 𝑐, 𝑑
𝐵 = {𝑐, 𝑑, 𝑒, 𝑓, 𝑔}
31

32. Solution:
𝐴 ∪ 𝐵 = {𝑎, 𝑏, 𝑐, 𝑑, 𝑒, 𝑓, 𝑔}
32
a
b
g
e
f
c
d
U
B
A

33. Intersection of Sets
 The intersection of two events is a set of
outcomes in both events.
Note that 𝐴 ∩ 𝐵 ≠ ∅
33
U
B
A

34. Example 1:
Let A is a natural number and a factor of 18
and B is a natural number and less than 6.
Find 𝐴 ∩ 𝐵.
34

35. Solution:
Given,
𝐴 = 1, 2, 3, 6, 9, 18
𝐵 = 1, 2, 3, 4, 5
𝐴 ∩ 𝐵 = {1, 2, 3}
35
4
5
1
2
3
6
9
18
U
B
A

36. Example 2:
Given,
𝑈 = 𝑎, 𝑏, 𝑐, 𝑑, 𝑒, 𝑓, 𝑔, ℎ, 𝑖
𝐴 = 𝑎, 𝑏, 𝑐, 𝑑, 𝑒
𝐵 = {𝑐, 𝑑, 𝑒, 𝑓, 𝑔, ℎ, 𝑖}
36

37. Solution:
𝐴 ∩ 𝐵 = {𝑐, 𝑑, 𝑒}
37
a
b
f
g
h
i
c
d
e

38. Mutually Exclusive and Inclusive Events
38
Mutually Exclusive
Events
 They have no
common
outcomes.
 They cannot occur
simultaneously.
 They cannot
happen at the same
time.
Mutually Inclusive
Events
 They have common
outcomes.
 They can occur
simultaneously.
 They can happen at
the same time..

39. Example 1:
Suppose a die is rolled. Let A be the event that
an even number turns up and let B be the
event that an odd number appears.
Determine the possible outcomes of events A
and B and draw a Venn diagram to illustrate
that they are mutually exclusive events.
39

40. Solution:
Given,
𝐴 = 2,4,6
𝐵 = {1,3,5}
In symbols, 𝐴 ∩ 𝐵 = ∅.
40
S
2
4
6
1
3
5
B
A

41. Example 2:
In a deck of 52 cards. Let A be the event that a
face cards and let B be the event that a spade
cards. Determine the possible outcomes of
events A and B and draw a Venn diagram to
illustrate that they are mutually exclusive
events.
41

42. Deck of Cards
42

43. Solution:
Given,
𝐴 = 12 𝑓𝑎𝑐𝑒 𝑐𝑎𝑟𝑑𝑠
𝐵 = {13 𝑠𝑝𝑎𝑑𝑒 𝑐𝑎𝑟𝑑𝑠}
In symbols, 𝐴 ∩ 𝐵 ≠ ∅.
43
S
9 face
cards
A B
10 spade
cards
3 face
cards

44. QUIZ TIME!
1. Find the intersection of events A and B and draw a
Venn diagram.
a. 𝐴 = {1, 2, 3, 4, 5} and 𝐵 = {3, 4, 5, 6}
b. 𝐴 = {1, 3, 6} and 𝐵 = {3, 6, 7, 8, 9}
c. 𝐴 = {2, 4, 6, 8} and 𝐵 = {1, 3, 5, 7, 9}
2. Illustrate the union of events A and B using a Venn
diagram.
a. 𝑆 = 1, 2, 3, 4, 5, 6, 7, 8, 9
𝐴 = {2, 4, 6} and 𝐵 = {6, 7, 8, 9}
b. 𝑆 = 1, 3, 5, 7, 9, 11
𝐴 = 1, 3, 5 and 𝐵 = {7, 9, 11}
44

45. Assignment:
Think about a situation wherein you can
apply union, events, and intersection. What
are you going to do is to:
■ Create a word problem about the
situation you think.
■ Answer your word problem and
present it in class.
45

46. “Thrift is not an affair of the pocket,
but an affair of character.”
-S. W. Straus
Thank you and God bless.