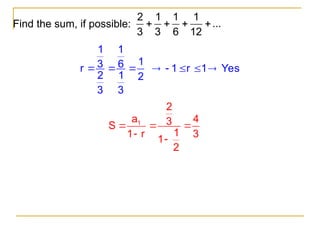
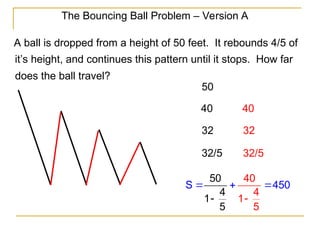
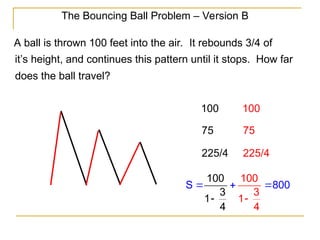
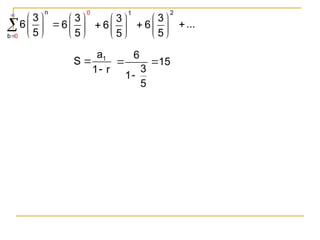
The document explains geometric sequences, characterized by a common ratio between consecutive terms, and provides methods to find their terms and sums. It includes examples illustrating how to calculate the nth term and the sum of finite geometric series, as well as sequences with distinct properties. Additionally, it discusses the use of summation notation to represent the sum of a sequence's terms.

1. Essential Question: What is a sequence
and how do I find its terms and sums?
How do I find the sum & terms of
geometric sequences and series?

2. Geometric Sequences
Geometric Sequence– a sequence whose
consecutive terms have a common ratio.

3. A sequence is geometric if the ratios of
consecutive terms are the same.
Geometric Sequence
3
2 4
1 2 3
.....
a
a a
r
a a a
   
The number r is the common ratio
ratio.

4. 2, 4, 8, 16, …, formula?, …
Ex. 1
12, 36, 108, 324, …, formula?, …
1, 4, 9, 16, …, formula? , …
Are these geometric?
1 1 1 1
, , , ,..., ?,...
3 9 27 61
formula
 
Yes 2n
Yes
4(3)n
No n2
No
(-1)n
/3

5. Finding the nth term of a Geometric
Sequence
an = a1rn – 1
r
a
a
 2
1

6. Ex. 2b
Write the first five terms of the
geometric sequence whose first
term is a1 = 9 and r = (1/3).
9 3 1
1
3
1
9
, , , ,

7. Ex. 3
Find the 15
Find the 15th
th
term of the geometric
term of the geometric
sequence whose first term is 20 and
sequence whose first term is 20 and
whose common ratio is 1.05
whose common ratio is 1.05
an = a1rn – 1
a15 = (20)(1.05)15 – 1
a15 = 39.599

8. Ex. 4 Find a formula for the nth term.
What is the 9th term?
5, 15, 45, …
an = 5(3)n – 1
an = 5(3)n – 1
a9 = 5(3)8
a9 = 32805
an = a1rn – 1

9. s
a r
r
n
n



1 1
1
( )
sum of a finite geometric series

10. Ex. 6 Find the sum of the first 12 terms of the
Find the sum of the first 12 terms of the
series 4(0.3
series 4(0.3)
)n
n
= 4(0.3)1
+ 4(0.3)2
+ 4(0.3)3
+ … + 4(0.3)12
r
r
a
a
S
n
n



1
1
1
3
.
0
1
)
3
.
0
(
2
.
1
2
.
1 12
12



S = 1.714

11. Ex. 7 Find the sum of the first 5 terms of the
Find the sum of the first 5 terms of the
series 5/3 + 5 + 15 + …
series 5/3 + 5 + 15 + …
r = 5/(5/3) = 3
r
r
a
a
S
n
n



1
1
1
3
1
)
3
(
3
5
3
5 5
5



S
= 605/3

12. 1, 4, 7, 10, 13, …. Infinite Arithmetic No Sum
3, 7, 11, …, 51 Finite Arithmetic  
n 1 n
n
S a a
2
 
1, 2, 4, …, 64 Finite Geometric
 
n
1
n
a r 1
S
r 1



1, 2, 4, 8, … Infinite Geometric
r > 1
r < -1
No Sum
1 1 1
3,1, , , ...
3 9 27
Infinite Geometric
-1 < r < 1
1
a
S
1 r



13. Find the sum, if possible:
1 1 1
1 ...
2 4 8
   
1 1
1
2 4
r
1
1 2
2
   1 r 1 Yes
    
1
a 1
S 2
1
1 r
1
2
  



14. Find the sum, if possible:
2 1 1 1
...
3 3 6 12
   
1 1
1
3 6
r
2 1 2
3 3
   1 r 1 Yes
    
1
2
a 4
3
S
1
1 r 3
1
2
  



15. Find the sum, if possible:
2 4 8
...
7 7 7
  
4 8
7 7
r 2
2 4
7 7
   1 r 1 No
    
NO SUM

16. Find the sum, if possible:
5
10 5 ...
2
  
5
5 1
2
r
10 5 2
   1 r 1 Yes
    
1
a 10
S 20
1
1 r
1
2
  



17. The Bouncing Ball Problem – Version A
A ball is dropped from a height of 50 feet. It rebounds 4/5 of
it’s height, and continues this pattern until it stops. How far
does the ball travel?
50
40
32
32/5
40
32
32/5
40
S 45
50
4
1
0
1
5
5
4
 




18. The Bouncing Ball Problem – Version B
A ball is thrown 100 feet into the air. It rebounds 3/4 of
it’s height, and continues this pattern until it stops. How far
does the ball travel?
100
75
225/4
100
75
225/4
10
S 80
100
4 4
3
1
0
1
0
3
 




20. The sum of the first n terms of a sequence is
represented by summation notation.
1 2 3 4
1
n
i n
i
a a a a a a

     
 
index of
summation
upper limit of summation
lower limit of summation
5
1
4n
n

 1 2 3 4 5
4 4 4 4 4
   
4 16 64 256 1024
    
1364


21.  
12
1
Example 6. Find the sum 4 0.3
n
n

Write out a few terms.
         
12
1 2 3 12
1
4 0.3 4 0.3 4 0.3 4 0.3 ... 4 0.3
n
n
    

 
1 4 0.3 0.3 and 12
a r n
   
 
12
1
1
1
4 0.3
1
n
n
n
r
a
r

 

  

 
  
 
12
1 0.3
4 0.3
1 0.3
 

  

 
 
1.714

If the index began at i = 0, you would have
to adjust your formula
     
12 12
0
0 1
4 0.3 4 0.3 4 0.3
n
n
i n
 
 
   
12
1
4 4 0.3
n
n
   4 1.714 5.714
  

22. 0
n
b
3
6
5


 

 
 

0
3
6
5
 
 
 
1
3
6
5
 
  
 
2
3
6
5
 
  
 
...

1
a
S
1 r


6
15
3
1
5
 
