The document provides information about hyperbolas including:
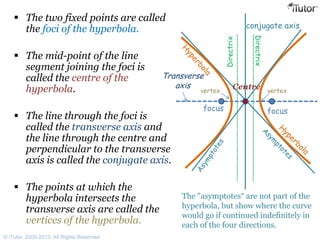
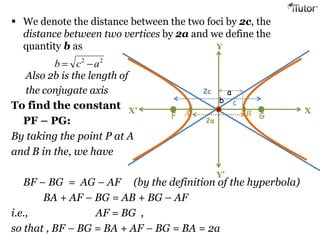
- A hyperbola is defined as the set of all points where the difference between the distances to two fixed points (foci) is a constant.
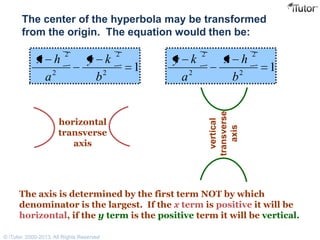
- Key properties include two foci, a transverse axis connecting the foci, a conjugate axis perpendicular to the transverse axis, and vertices where it intersects the transverse axis.
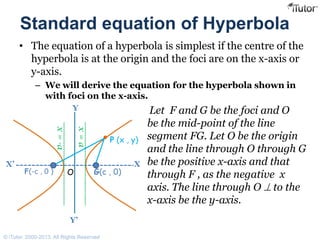
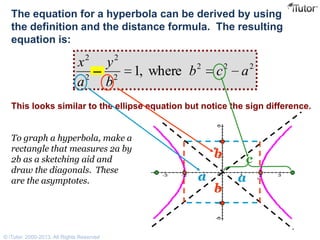
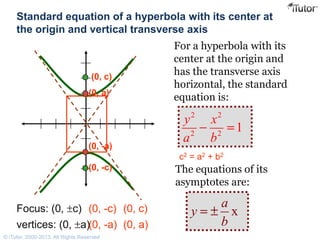
- The standard equation of a hyperbola with foci on the x-axis is (y2/b2) - (x2/a2) = 1, where a and b are related to the distances between the foci and vertices.