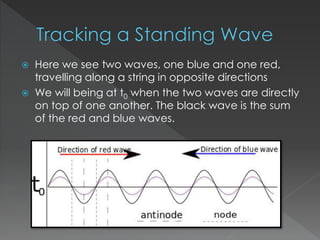
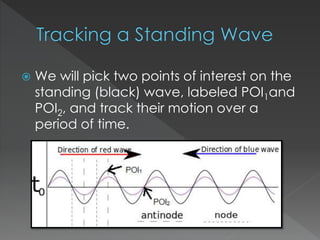
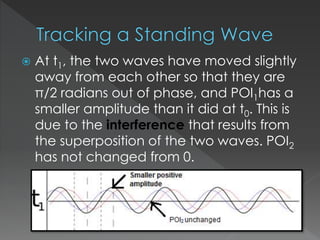
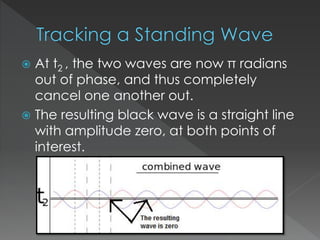
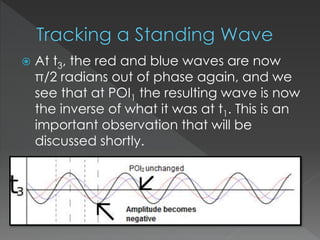
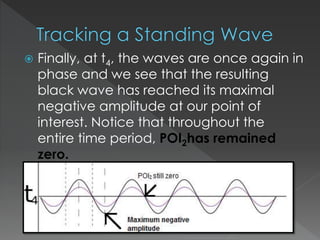
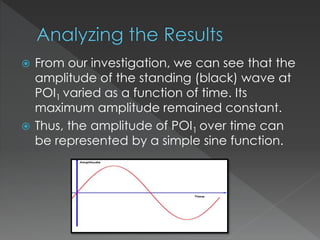
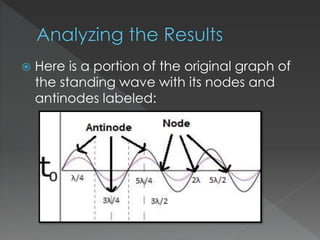
This document explores the behavior of standing waves, which are formed by the interference of two waves traveling in opposite directions. It discusses how the amplitude at fixed points on a standing wave varies over time, identifying points of interest as nodes (where amplitude is always zero) and antinodes (where maximum amplitude occurs). The document concludes that the amplitude of points on a standing wave oscillates sinusoidally, with nodes located at specific intervals.

2.  In this Learning Object we will look at
how the amplitudes of two fixed positions
on a standing wave change with time.

3.  In this Learning Object we will look at
how the amplitudes of two fixed positions
on a standing wave change with time.
 But what are standing waves?

4.  In this Learning Object we will look at
how the amplitudes of two fixed positions
on a standing wave change with time.
 But what are standing waves?
 A standing wave results when two waves
that have the same frequency and
amplitude travel in opposite directions
along the same medium.

5.  A standing wave is therefore the sum of the
two waves travelling in opposite directions,
and can be expressed by adding the wave
functions of the two component waves.
 The equation of the standing wave is thus
D(x,t)=D1(x,t)+D2(x,t)
 Using this information, we can track the
motion of a standing wave by looking at
the motion of its component waves at a
fixed position.

6.  Here we see two waves, one blue and one red,
travelling along a string in opposite directions
 We will being at t0 when the two waves are directly
on top of one another. The black wave is the sum
of the red and blue waves.

7.  We will pick two points of interest on the
standing (black) wave, labeled POI1and
POI2, and track their motion over a
period of time.

8.  At t1, the two waves have moved slightly
away from each other so that they are
π/2 radians out of phase, and POI1has a
smaller amplitude than it did at t0. This is
due to the interference that results from
the superposition of the two waves. POI2
has not changed from 0.

9.  At t2 , the two waves are now π radians
out of phase, and thus completely
cancel one another out.
 The resulting black wave is a straight line
with amplitude zero, at both points of
interest.

10.  At t3, the red and blue waves are now
π/2 radians out of phase again, and we
see that at POI1 the resulting wave is now
the inverse of what it was at t1. This is an
important observation that will be
discussed shortly.

11.  Finally, at t4, the waves are once again in
phase and we see that the resulting
black wave has reached its maximal
negative amplitude at our point of
interest. Notice that throughout the
entire time period, POI2has remained
zero.

12.  From our investigation, we can see that the
amplitude of the standing (black) wave at
POI1 varied as a function of time. Its
maximum amplitude remained constant.
 Thus, the amplitude of POI1 over time can
be represented by a simple sine function.

13.  However, our POI2 never moved from the
zero position. Its amplitude as a function
of time was always equal to zero.
 We can conclude from our investigation
that the amplitude of any point on the
standing wave will vary as a sinusoidal
function with respect to time.
 However, certain points along the wave,
such as our POI2, have constant zero
amplitude.

14.  We call those points “nodes” and they
occur at every location x=mλ/2, where
m is any integer value.
 Our other point, POI1, is an example of
what is called an “antinode”, which is
any point where the standing wave
reaches a maximum amplitude. They
occur at every location x=(m+1/2)(λ/2),
where m is any integer value.

15.  Here is a portion of the original graph of
the standing wave with its nodes and
antinodes labeled:

16.  Just like our two points of interest, every
point on the standing wave (over the
course of one wavelength) has its own
unique maximum amplitude, and it
oscillates from its positive to its negative
maximum amplitude
 This is different from travelling waves, in
which every point on the wave oscillates
with the same amplitude

17.  Question 1:
A sinusoidal standing wave has a
wavelength equal to π/2. Where are its
first 4 nodes located?

18.  Answer:
A standing wave has nodes at every point
x=mλ/2. The first node will have the lowest
possible value of m, which is zero. Therefore,
the first node occurs at x=0. Each
consecutive node will have a value of m
one greater than the last. That gives us the
second node at x=(0+1)(π/2)(1/2)= π/4, the
third node at x=(1+1)(π/2)(1/2)= π/2 and
the fourth node at x=(2+1)(π/2)(1/2)= 3π/4

19.  Question 2:
Find the locations of the first 4 antinodes
of the standing wave in the previous
problem.

20.  Answer:
The antinodes of a standing wave are
located at every point x=(m+1/2)(λ/2).
Therefore, as previously, the first antinode is
found at the lowest value of m:
x=(0+1/2)(π/2)(1/2)= π/8. The second
antinode will be at
(0+1+1/2)(π/2)(1/2)=3π/8. The third
antinode is found at (1+1+1/2)(π/2)(1/2)=
5π/8 and the fourth antinode at
(2+1+1/2)(π/2)(1/2)= 7π/8

21.  Pictures from:
 http://www.minelab.com/__files/i/5894/S
ineWave.gif
 http://en.wikipedia.org/wiki/Standing_w
ave#mediaviewer/File:Standingwaves.sv
g