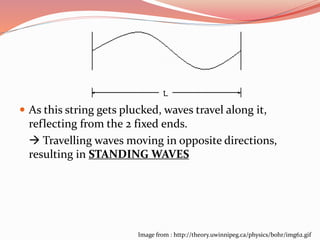
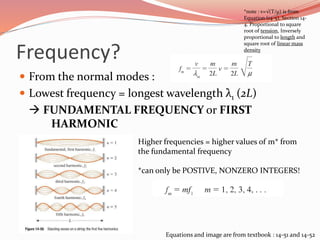
This document summarizes key concepts about standing waves on a vibrating string. It explains that standing waves result from traveling waves reflecting off of fixed ends of the string. The normal modes of the string determine the possible wavelengths and frequencies. The document provides equations to calculate the wavelength and frequency of a string vibrating at a particular harmonic. It then works through an example problem, finding the wavelength and frequency of a string vibrating at the fourth harmonic.

1. Physics 101 Learning Object (LO6)
By: James Kurniawan

2.  As this string gets plucked, waves travel along it,
reflecting from the 2 fixed ends.
 Travelling waves moving in opposite directions,
resulting in STANDING WAVES
Image from : http://theory.uwinnipeg.ca/physics/bohr/img62.gif

3. Wavelength?
 Because string is clamped at both ends: Amplitude
must be 0 at x=0 and x=L -
 and
 Rearranging and simplifying the equation above :
 These standing waves = NORMAL MODES of
vibration of string
*longest wavelength possible is 2L.
*m = essentially ANTINODES
Equations are from textbook: 14-48 to 14-50
*m can only be a positive,
nonzero INTEGER

4. Frequency?
 From the normal modes :
 Lowest frequency = longest wavelength λ1 (2L)
 FUNDAMENTAL FREQUENCY or FIRST
HARMONIC
*note : v=√(T/µ) is from
Equation (14-5), Section 14-
4. Proportional to square
root of tension, Inversely
proportional to length and
square root of linear mass
density
Higher frequencies = higher values of m* from
the fundamental frequency
*can only be POSTIVE, NONZERO INTEGERS!
Equations and image are from textbook : 14-51 and 14-52

5. Harmonics
 Allowed frequencies (where f=mf , and m = integers) =
HARMONICS or RESONANT FREQUENCIES
 A string can vibrate in a single normal mode or in
several modes
Equation is from textbook : 14-54

6. Question
 The string on the bottom is 5.0 meters long and is
vibrating as the fourth harmonic. Its linear mass
density is 4.25 x 10^-3 kg/m. The tension in the string
is kept at 60.0N.
 Find its wavelength and frequency.
Picture from :
http://www.physicsclassroom.com/class/waves/Lesson-
4/Mathematics-of-Standing-Waves

7. Answer (Part 1)
1) Wavelength:
Using Equation (14-50) : λm = 2L/m
- m = 4, L = 5.0 m
 λ4 = 2(5.0)/(4) = 2.5 m

8. Answer (Part 2)
2) Frequency :
Using Equation (14-51) : fm = m/2L * √(T/µ)
- m = 4, L = 5.0 m, T = 60.0 N,
µ = 4.25 x 10^-3 kg/m
 f4 = (4)/2(5.0) * √(60.0/4.25 x 10^-3)
= 47.5 Hz