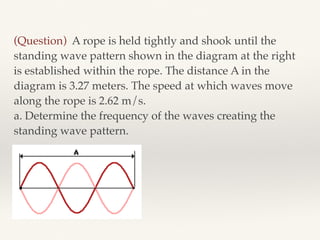
The document explains the concept of standing waves, which occur when two harmonic waves of equal amplitude and frequency move in opposite directions, resulting in a fixed pattern of nodes and antinodes. It describes the mathematical formulation of standing waves and how the amplitude varies with position, producing points of no movement (nodes) and points of maximum amplitude (antinodes). An example is provided to demonstrate the calculation of frequency from the wave speed and wavelength.

1. Learning Object 6
Standing Waves By David Park

2. Standing Waves
❖ A Standing wave is two harmonic waves with equal
amplitude, wavelength and frequency that are moving
in the opposite direction of each other.
❖ For mathematical simplicity, we assume that phase
constant for both waves are zero.
❖ However, the general case is that the phase constant for
the two waves may be unequal.

3. Standing Waves
❖ The waves functions for the two opposing waves are:
D1(x,t)=Asin(kx-wt)
(For the wave moving in the direction of increasing x)
D2(x,t)=Asin(kx+wt)
(For the wave moving in the direction of decreasing x)

4. ❖ When you apply the principal of superposition* the
result is a wave function:
D(x,t)=D1(x,t)+D2(x,t)
=A sin(kx-wt)+A sin(kx+wt)
=A[sin(kx-wt)+sin(kx+wt)]
❖ Using the trigonometric identity
sin(a-b)+sin(a+b)=2sin(a)*cos(b), where a=kx and b=wt
D(x,t)=2Asin(kx)*cos(wt)
*(Superposition) When more than one wave is present in a medium at the same time,
the resultant wave at any point in the medium is equal to the algebraic sum of the
waves at that point

5. Travelling wave vs. Standing Wave
❖ This equation may seem similar to a travelling wave,
however a travelling wave must have the position x and
time t together in the form x∓vt, where v is the wave
speed.
❖ In the equation D(x,t)=2Asin(kx)*cos(wt) the x and t
variable are separate, with x in the sine function and t in
the cosine. Differentiating the two

6. ❖ D(x,t)=2Asin(kx)*cos(wt)
with this equation, we can define a position-dependant
amplitude A(x):
A(x)=2A sin(kx)=2A sin(2!(x/λ))
❖ Using that equation, we can rewrite
D(x,t)=2Asin(kx)*cos(wt)
D(x,t)=A(x) cos(wt)

7. ❖ When two waves of equal
wavelength, frequency and
amplitude but moving in opposite
directions combine,each segment of
the wave oscillates in a simple
harmonic motion.
❖ The frequency and amplitude
depends on the location of the
segment along the wave
❖ All other points have amplitudes
between zero and 2A and any two
points that are one wavelength apart
have the same amplitude because of
the formula:
A(xo+λ)=2A sin(2!((xo+λ)/λ))
=2A sin(2!(xo/λ)+2!)
=2A sin(2!(xo/λ) = A(xo)
❖ The figure above shows
a plot of A(x) as a
function of position.
Where the amplitude is
a sine function, so
certain points on the
wave have zero
amplitude and remain
at rest at all times.
These points are called
nodes. The min/max
points are called
antinodes

8. Location of Nodes and Antinodes
❖ At the nodes of a standing wave, A(x)=0 therefore, nodes occur when
sin((2!/λ)x)=0
(2!/λ)x=m! m=0, ±1, ±2,…
x=m(λ/2) m=0, ±1, ±2,…
x=0, ±(λ/2), ±λ, ±(3λ/2), ±2λ,…
❖ Thus, the distance between two consecutive nodes is half a wavelength
❖ At the anti nodes of a standing wave, A(x) = ±2A, which occurs when
sin((2!/λ)x)= ±1
(2!/λ)x=(m+(1/2))! m=0, ±1, ±2,…
x=(m+(1/2))(λ/2) m=0, ±1, ±2,…
x=±(λ/4), ±(3λ/4), ±(5λ/4),…
❖ The distance between consecutive antinodes is also half a wavelength.
An adjacent node and antinode are a quarter of a wavelength apart.

9. ❖ To see how a wave oscillates in standing wave pattern we use the wave function
in terms of the time period:
D(x,t)=2A sin((2!/λ)x)*cos((2!/T)t)
❖ All points between two consecutive nodes oscillate in phase with each other. The
antinode has the greatest mean speed as it has to cover the longest distance (8A)
in one period. The speed decreases the further away from the antinode and is
zero at the nodes.
❖ Note: the motion of the sections between the next two nodes is ! rad out of phase
with the first section
❖ The sine term in the wave function accounts for this property:
A(xo+(λ/2))=2A sin((2!/λ)*(xo+(λ/2)))
=2A sin((2!/λ)xo)+!
=-2A sin((2!(λ/xo))
=-A(xo)

10. ❖ The figure beside shows the displacement of
a section of the oscillating string at intervals
of T/8 from T=0 to t=T/2.
❖ The table below compares the displacements
of the section of the wave between the first
two nodes during the first half of a cycle.
The motion for the next half of the period is in the opposite
direction. This oscillatory motion repeats every cycle.

11. EXAMPLE

12. (Question) A rope is held tightly and shook until the
standing wave pattern shown in the diagram at the right
is established within the rope. The distance A in the
diagram is 3.27 meters. The speed at which waves move
along the rope is 2.62 m/s.
a. Determine the frequency of the waves creating the
standing wave pattern.

13. ❖ Answer: 1.20Hz
❖ Since we’re given the velocity (v=2.62m/s)
we can use the formula: v=f*λ and then rearrange it to find
f. f=v/λ
❖ Looking at the graph of the wave we can see that there are
3/2 of a wave, so we equate that to the given distance,
3.27m = (3/2)λ, which equates to
λ = 2.18m
❖ Plugging in the values back into f=v/λ, we get 2.62/2.18
to get 1.20Hz

14. ❖ Diagrams and tables all taken from Physics for Scientists
and Engineers textbook.
❖ Example taken off of
http://www.physicsclassroom.com/calcpad/waves/
prob18.cfm