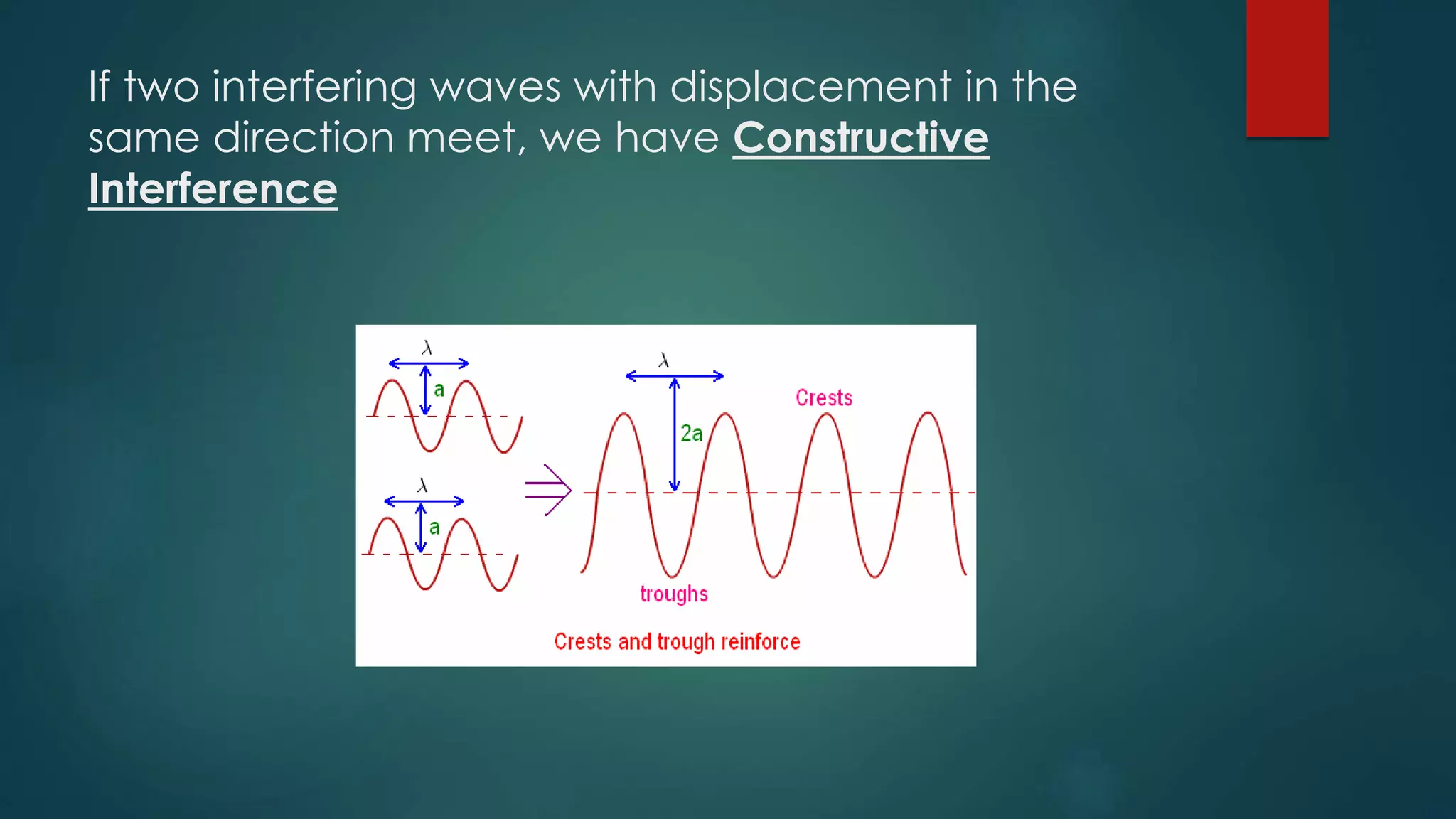
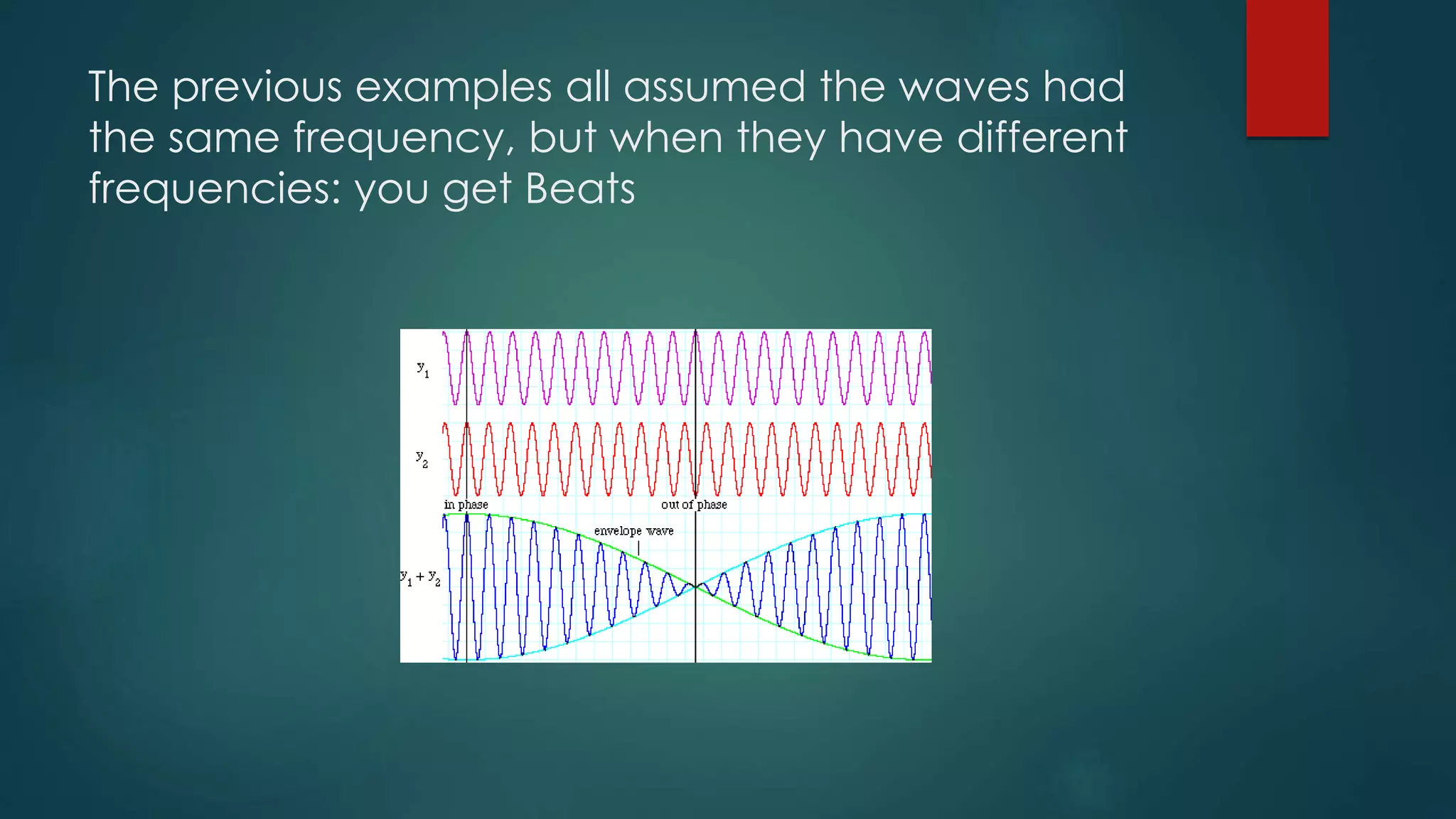
Beats occur when two sounds waves of similar but not identical frequencies interfere with each other. The difference in frequencies produces a fluctuation in volume that is heard as a periodic pulsing known as the beat frequency. Beats are caused by constructive and destructive interference between waves. When calculating beats, the beat frequency is equal to the difference between the two sound wave frequencies. The average frequency heard is equal to the sum of the frequencies divided by two. Interfering waves of different frequencies will produce a new wave with an amplitude equal to twice the amplitude of the original waves.

1. Beats
PHYS 101

2. What are Beats?
 Beats are what result when there is interfering waves with
similar, but not identical, frequencies.
 The difference in frequencies produces a fluctuation in
the volume at a rate determined by the difference
between the frequencies.
 Beats are generally measured by their frequency in hertz
units (Hz).

3. Interference
 To understand how Beats work, we must first understand
the nature of wave interference in sound.
 When two waves meet, their amplitudes will combine to
form a new wave temporarily with a different amplitude.
 The resulting new wave that is created varies depending
on whether the wave displacement of each wave is in
the same or opposite direction of the other.

4. If two interfering waves with displacement in the
same direction meet, we have Constructive
Interference

5. If two interfering waves with displacement in
opposing directions meet, we have Destructive
Interference

6. The previous examples all assumed the waves had
the same frequency, but when they have different
frequencies: you get Beats

7. How to calculate the beat
frequency:
 To calculate the beat frequency, you need to
find the difference between the two
frequencies.
 ƒ1 - ƒ2 = ƒbeat
 The beat will tell you how many times an
observer will hear the beat per second.

8. The resulting sound from a beat:
 When the two interfering wave frequencies are close enough, an
observer will not hear two different frequencies.
 Instead, they will produce a sound that is equal to the average of
the frequencies of the two different waves.
 The frequency of the sound that we observe can be calculated by
finding the average frequency of the two waves like so:
 ƒavg. = (ƒ1 + ƒ2)/2
or
ƒavg. = (ƒ1 + ƒ2 + … ƒn)/ n waves

9. Calculating the Amplitude:
 If the frequencies were the same, the amplitude of the waves could
be calculated as so:
 y = y1 + y2 = A(cos(2πƒ1t) + cos(2πƒ2t)
 A represents the wave amplitude
 ƒ represents the wave frequencies
 t represents time
 y represents the vertical displacement of each wave

10. Calculating the Amplitude
continued…
 By using the following equation:
cos a + cos b = 2 cos ((a-b)/2)cos((a+b)/2)
 We can rewrite the equation to incorporate the different
frequencies to find the new amplitude with this equation:
y = 2A*cos2π((ƒ1 - ƒ2)/2)*t)*cos2π((ƒ1 + ƒ2)/2)*t)
 This can be further simplified to:
y = 2A*cos2π((ƒ1 - ƒ2)/2)*t

11. Problem #1
 When it comes to interfering waves with different frequencies, the
beat frequency will usually be larger than the average frequency.
 A. True
 B. False

12. Problem #1 – Solution
 The answer is false, the beat frequency is the difference between
the frequencies of the interfering waves and since the difference is
between two wave frequencies needs to be small to produce
beats, the beat frequency will be small. The average frequency on
the other hand is the average of the two waves and will be a
number similar to the frequency of each individual wave. As a result,
in the vast majority of scenarios, the average frequency will be
larger than the beat frequency.

13. Problem #2
 Two waves are interfering and producing a sound at 328 Hz 4 times
a second.
 i.) What are the individual frequencies of each of the waves?
 ii.) Assuming they have the same amplitude, what would be the
new amplitude of the interfering waves?
 iii.) Suppose to the two waves had the same frequency, what would
the new beat frequency be?

14. Problem #2 - Solutions
 i.) Since the frequency of the sound produced is the average of the
frequencies of the two waves, that tells us that the sound produced
is between the frequencies of the two waves.
 We also know that the sound is being produced 4 times a second,
which also tells us the beat frequency if 4 Hz.
 Since the beat frequency is the difference between the two wave
frequencies and we know that the average frequency is 328 Hz, this
tells us that one frequency will be 2 Hz higher and the other will be 2
Hz lower.
 The resulting answer is that one wave is 330 Hz and the other is 326
Hz.

15. Problem #2 - Solutions
 ii.) We know that the amplitudes of the two waves are the same,
which means this equation previously mentioned in the notes
applies to this problem:
 y = 2A*cos2π(((ƒ1 - ƒ2)/2)*t
 We also determined from part i.) that the frequency of the two
waves were 330 Hz and 326 Hz respectively.
 Since we know Amplitude and time for both waves are the same,
we can eliminate both of those to produce the following equation:
 y = 2*cos2π((330 - 326)/2)
 This produces the resulting amplitude of 2, i.e. twice the amplitude
of one of the waves.

16. Problem # 2 - Solutions
 iii.) While the answer would technically be 0, this means that in
reality there would be no beat frequency or beats since they are
only present when there is a difference between the frequencies of
the interfering waves, which would not be the case if they both had
the same frequency.

17. Sources Cited
Source of Wave Images:
 http://physics.tutorvista.com/waves/constructive-interference.html
 http://www.animations.physics.unsw.edu.au/jw/beats.htm
Source of equations, definitions, and facts:
 Physics for Scientists and Engineers - An Interactive Approach