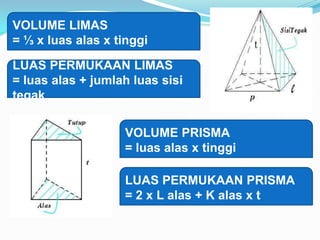
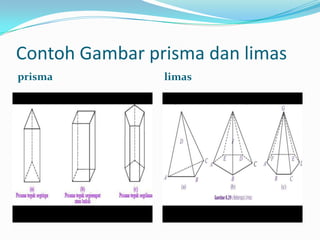
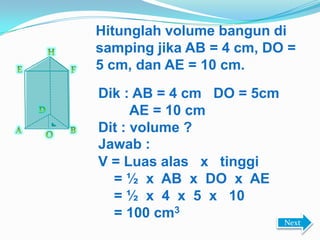
Dokumen ini menjelaskan tentang bangun ruang prisma dan limas, termasuk jenis serta rumus-rumus yang terkait dengan masing-masing bangun. Prisma memiliki sepasang bidang sejajar dan limas ditandai dengan puncak runcing, dengan rumus untuk volume dan luas permukaannya. Contoh perhitungan volume diberikan untuk kedua jenis bangun ruang ini.

1. Bangun Ruang Prisma dan Limas

2. Prisma
 Prisma adalah bangun ruang yang memiliki sepasang
bidang sejajar dan kongruen yang merupakan alas dan
tutup. Sedangkan bidang-bidang lainnya diperoleh
dengan menghubungkan titik-titik sudut dari dua
bidang yang sejajar. Jenis prisma ada beberapa macam
yang diberi nama sesuai bentuk alas prisma.

3. Limas
 Bangun 3-Dimesi yang dibatasi oleh bangun segitiga
sebagai sisi tegaknya. Biasa menyebutnya sebagai
bangun ruang. Ciri khas limas adalah memiliki bagian
runcing di bagian atasnya sebagai titik puncak.

4. Rumus (Prisma)
 Titik sudut : 2n
 Sisi (bidang) : n+2
 Rusuk : 3n
 Diagonal Bidang / Sisi : n(n-1)
 Diagonal Ruang : n(n-3)
 Bidang Diagonal : ½ n(n-1)
 Panjang Kerangka : jumlahkan rusuk
 Luas Permukaan : (2.La) + (Ka.t)
 Volume : La.t

5. Rumus (Limas)
 Titik sudut : n+1
 Sisi (bidang) : n+1
 Rusuk : 2n
 Diagonal Bidang / Sisi : 1/2n(n-3)
 Diagonal Ruang : -
 Bidang Diagonal : 1/2n(n-3)
 Panjang Kerangka : jumlahkan rusuk
 Luas Permukaan : jumlahkan luas sisinya
 Volume : 1/3.La.t

6. VOLUME LIMAS
= ⅓ x luas alas x tinggi
LUAS PERMUKAAN LIMAS
= luas alas + jumlah luas sisi
tegak
VOLUME PRISMA
= luas alas x tinggi
LUAS PERMUKAAN PRISMA
= 2 x L alas + K alas x t

7. Contoh Gambar prisma dan limas
prisma limas

8. Contoh salah satu Jaring-jaring
Prisma Limas

9. A
9 cm
5 cm
D c
B
T
Hitungla
h
volumek
u
Penyelesaian:
Dik :
s = 5 cm
t = 9 cm
Dit : volume ?
Jawab :
V = 1/3 x luas alas x
tinggi
V = 1/3 x s2 x t
V = 1/3 x 52 x 9
V = 1/3 x 25 x 9
V = 25 x 3
V = 75 cm3
Next

10. Hitunglah volume bangun di
samping jika AB = 4 cm, DO =
5 cm, dan AE = 10 cm.
Dik : AB = 4 cm DO = 5cm
AE = 10 cm
Dit : volume ?
Jawab :
V = Luas alas x tinggi
= ½ x AB x DO x AE
= ½ x 4 x 5 x 10
= 100 cm3
Next

11. Selesai