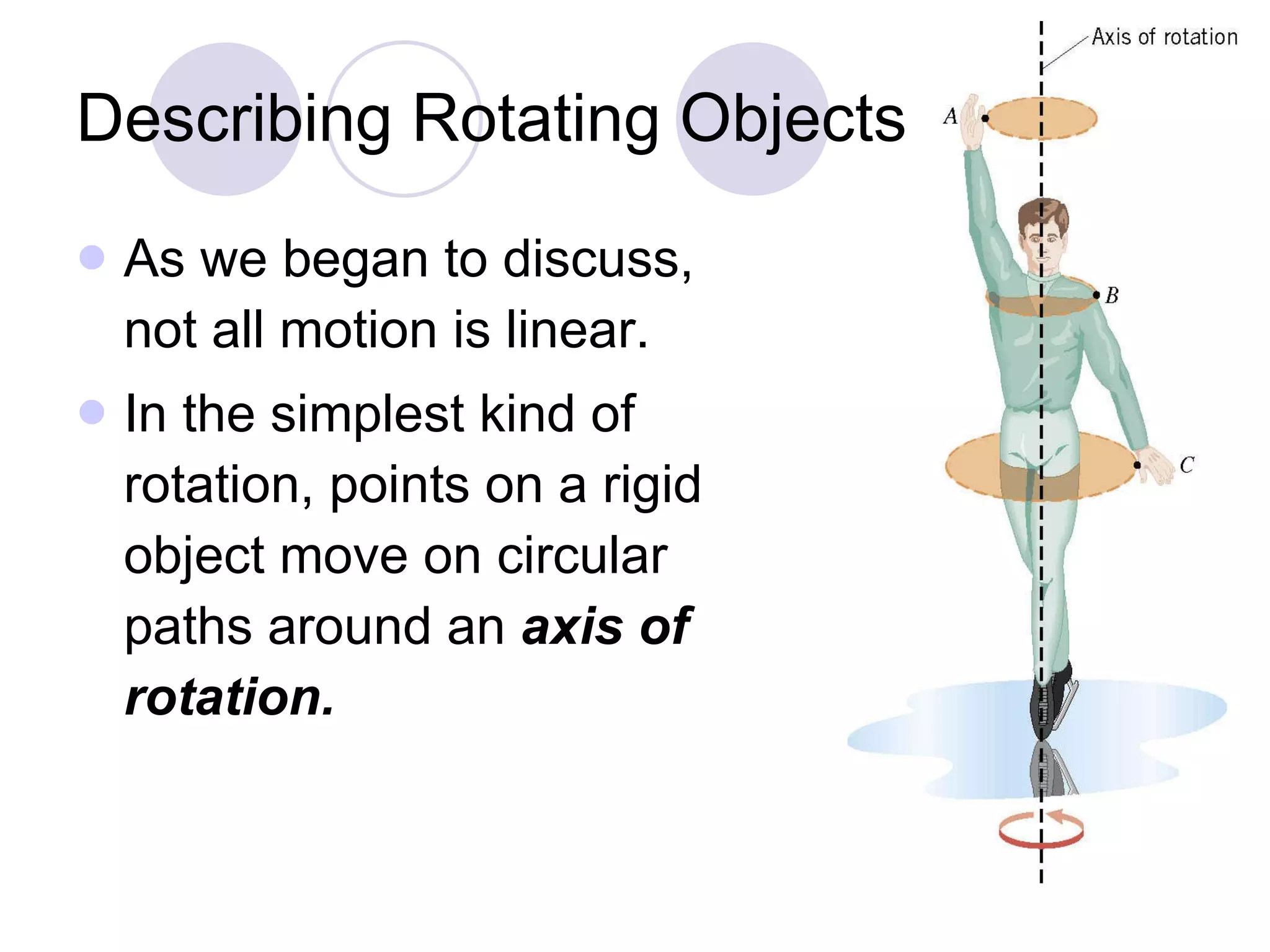
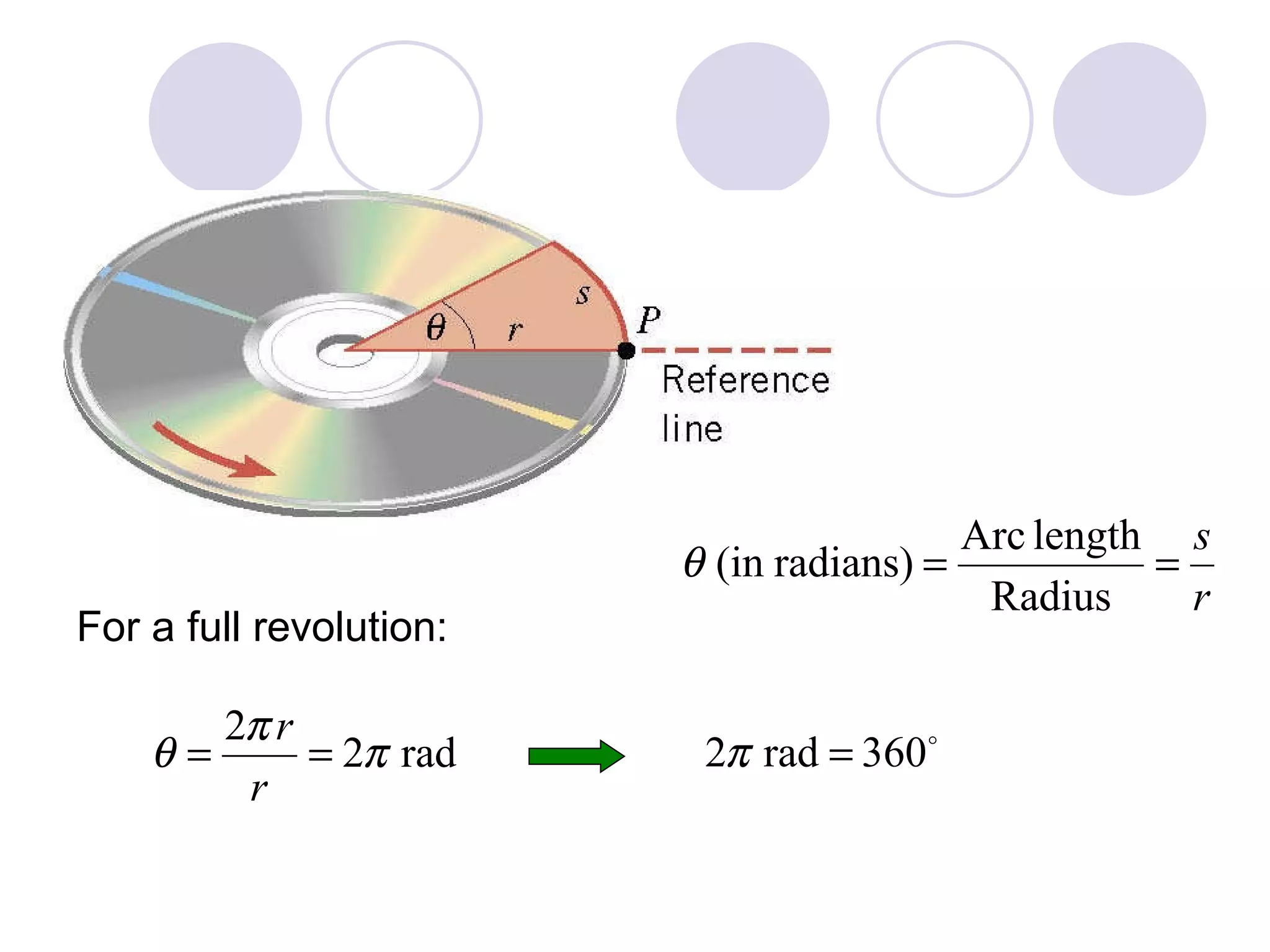
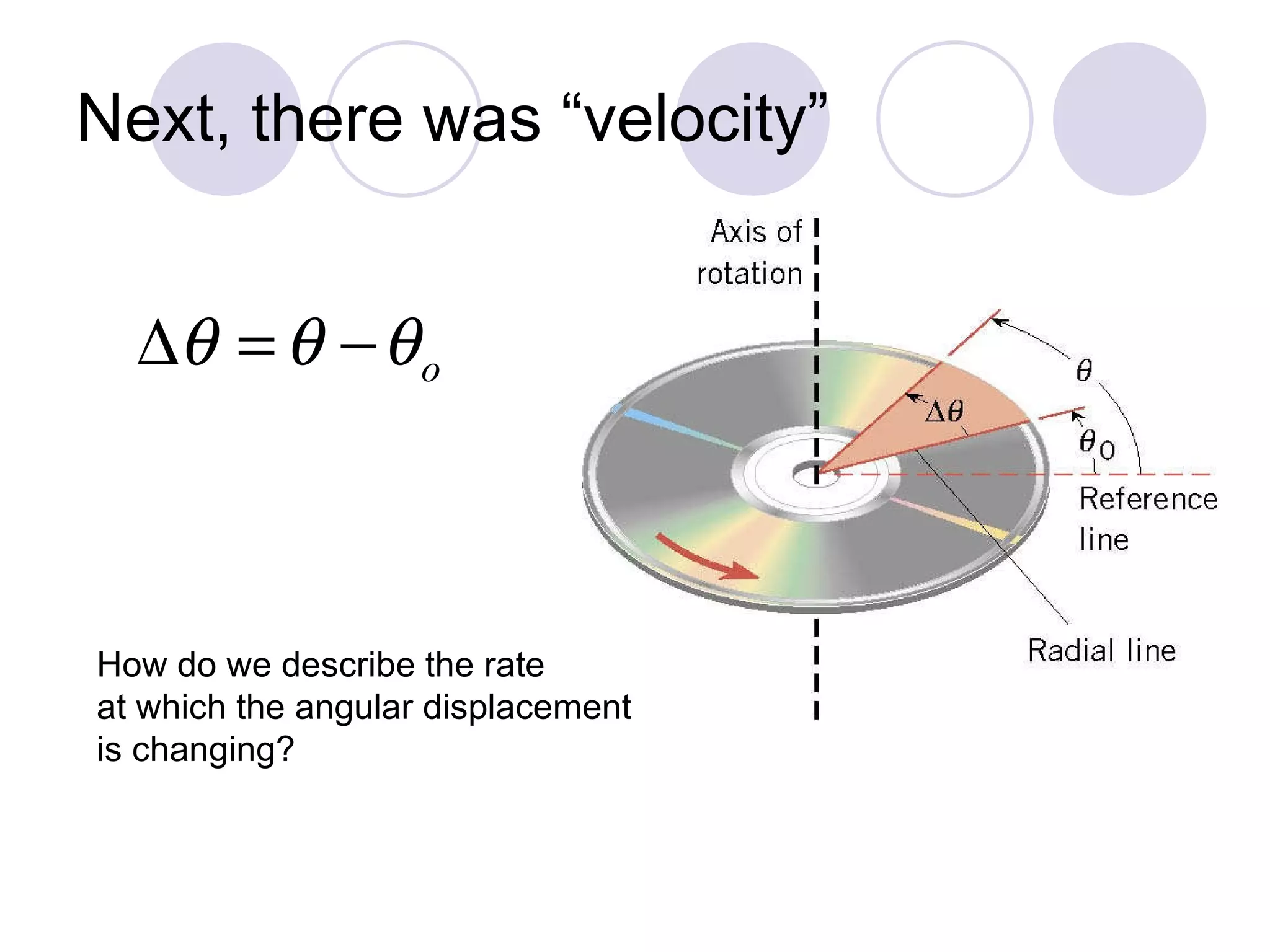
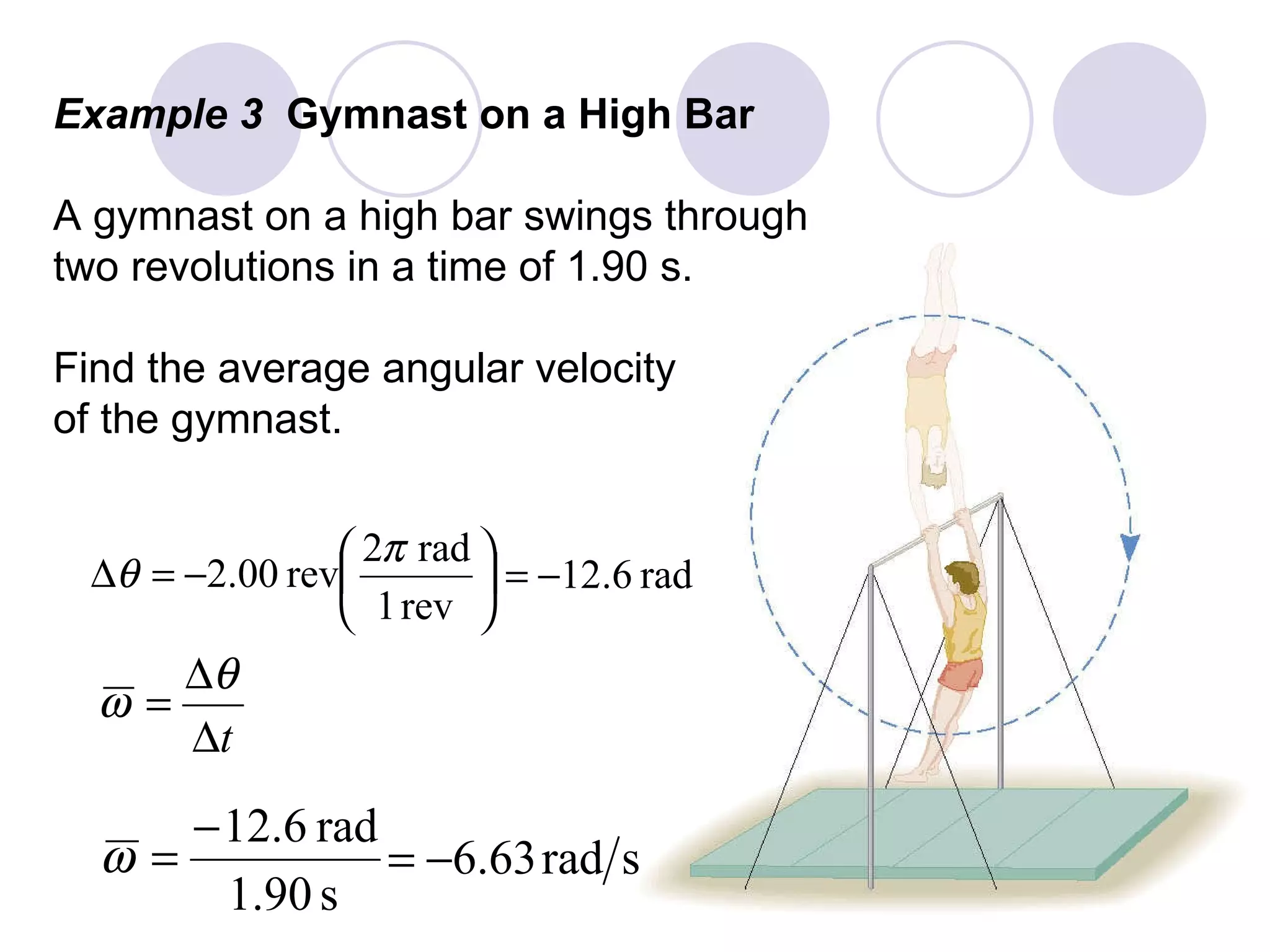
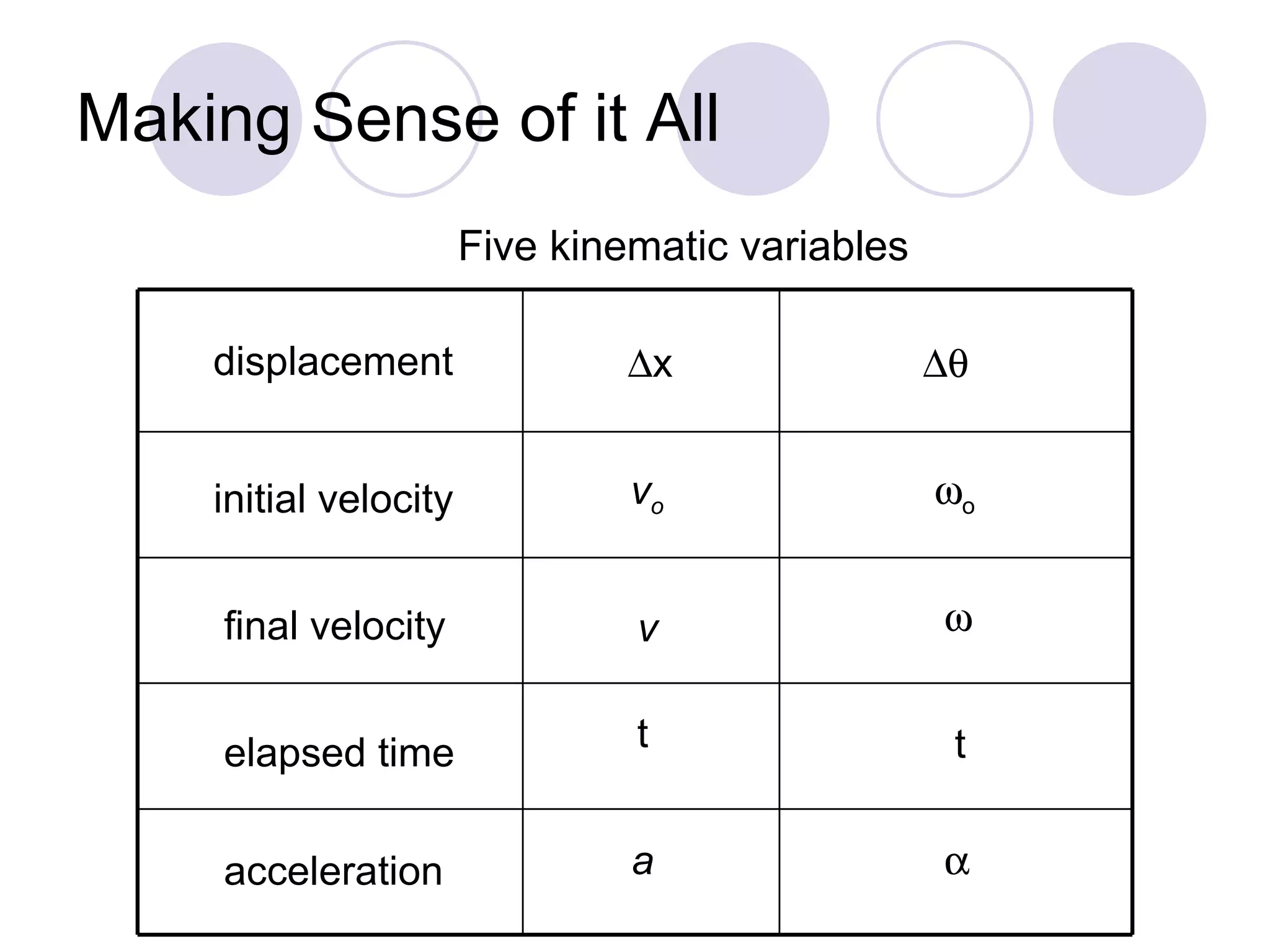
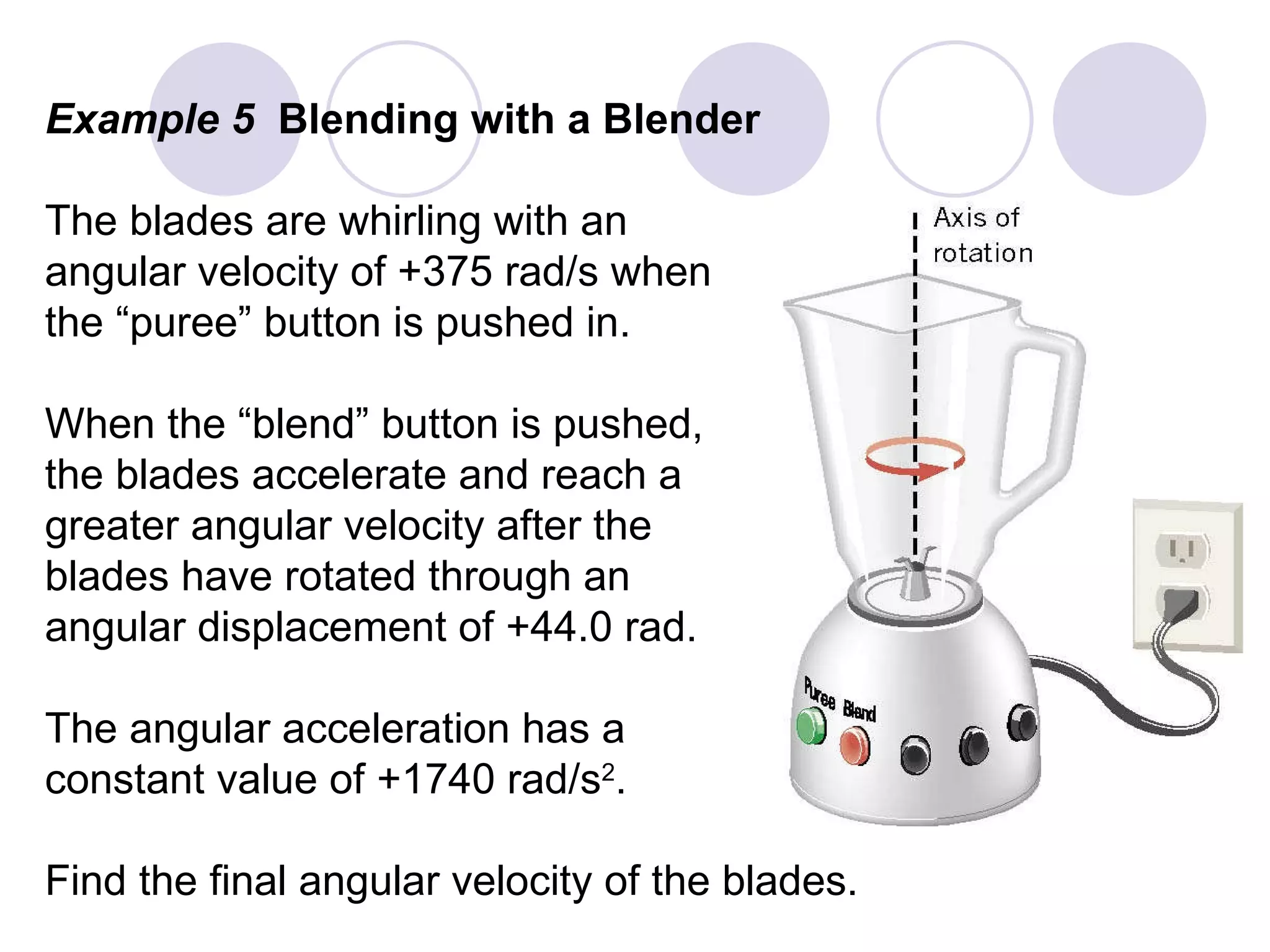
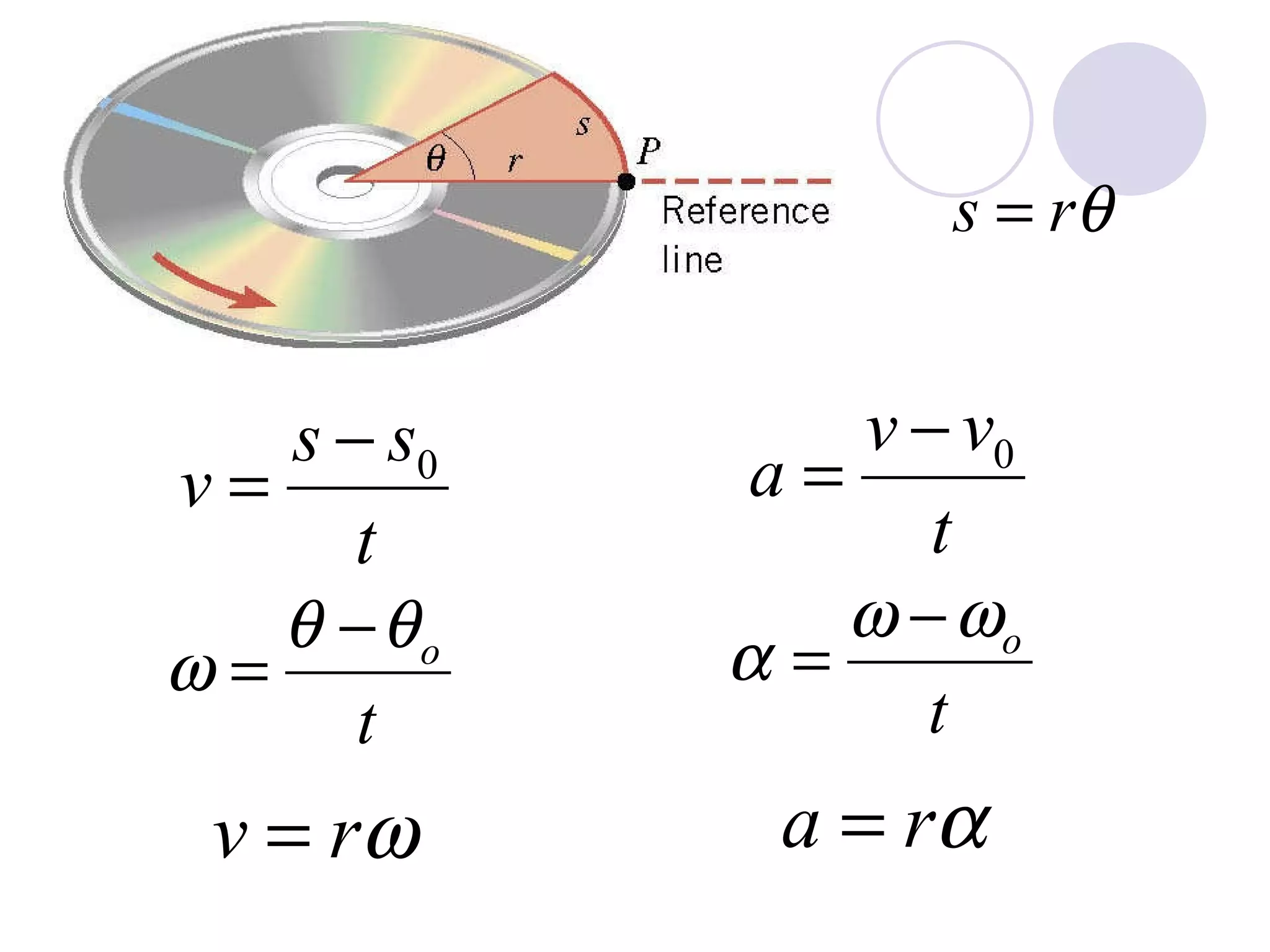
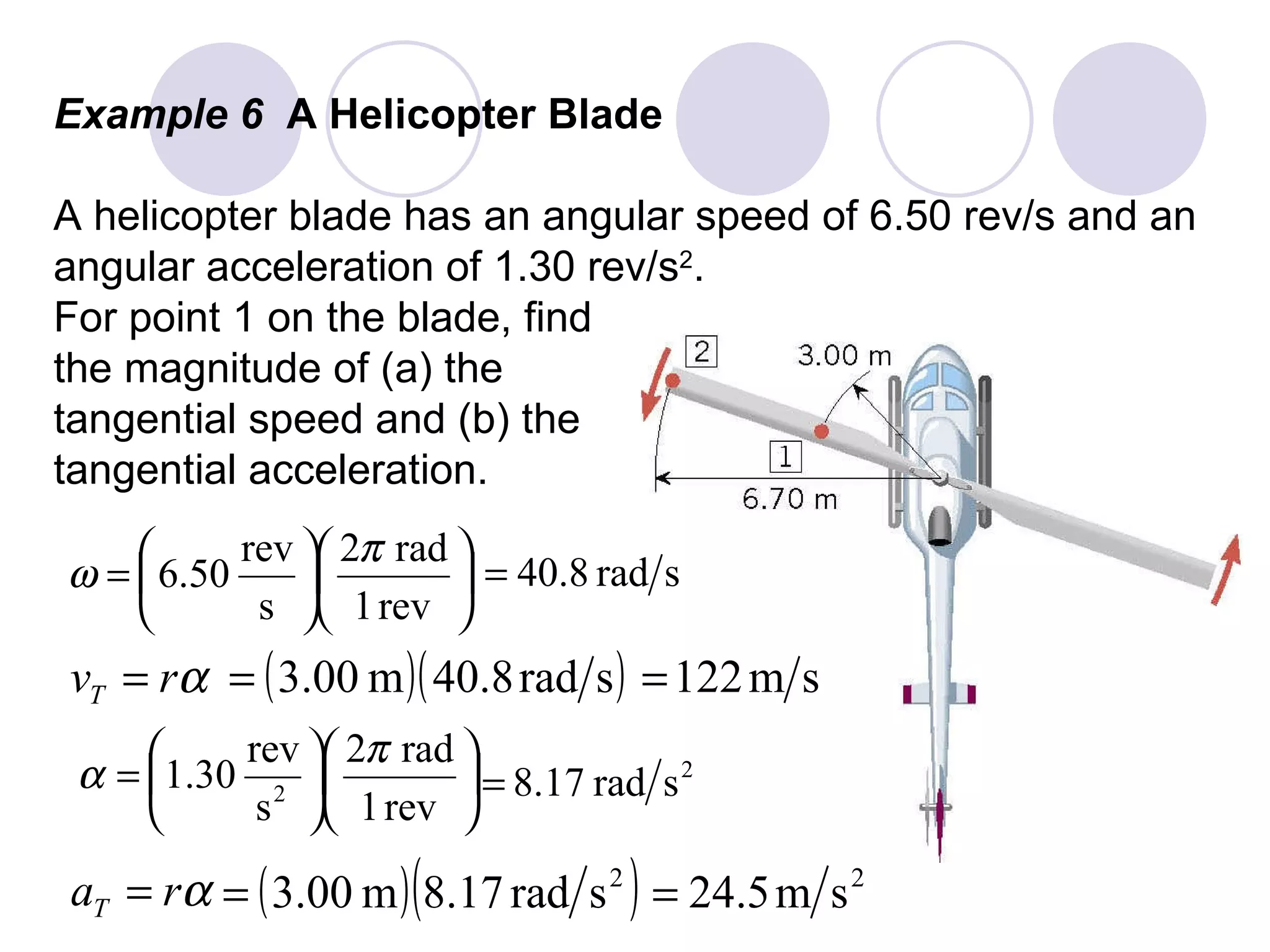
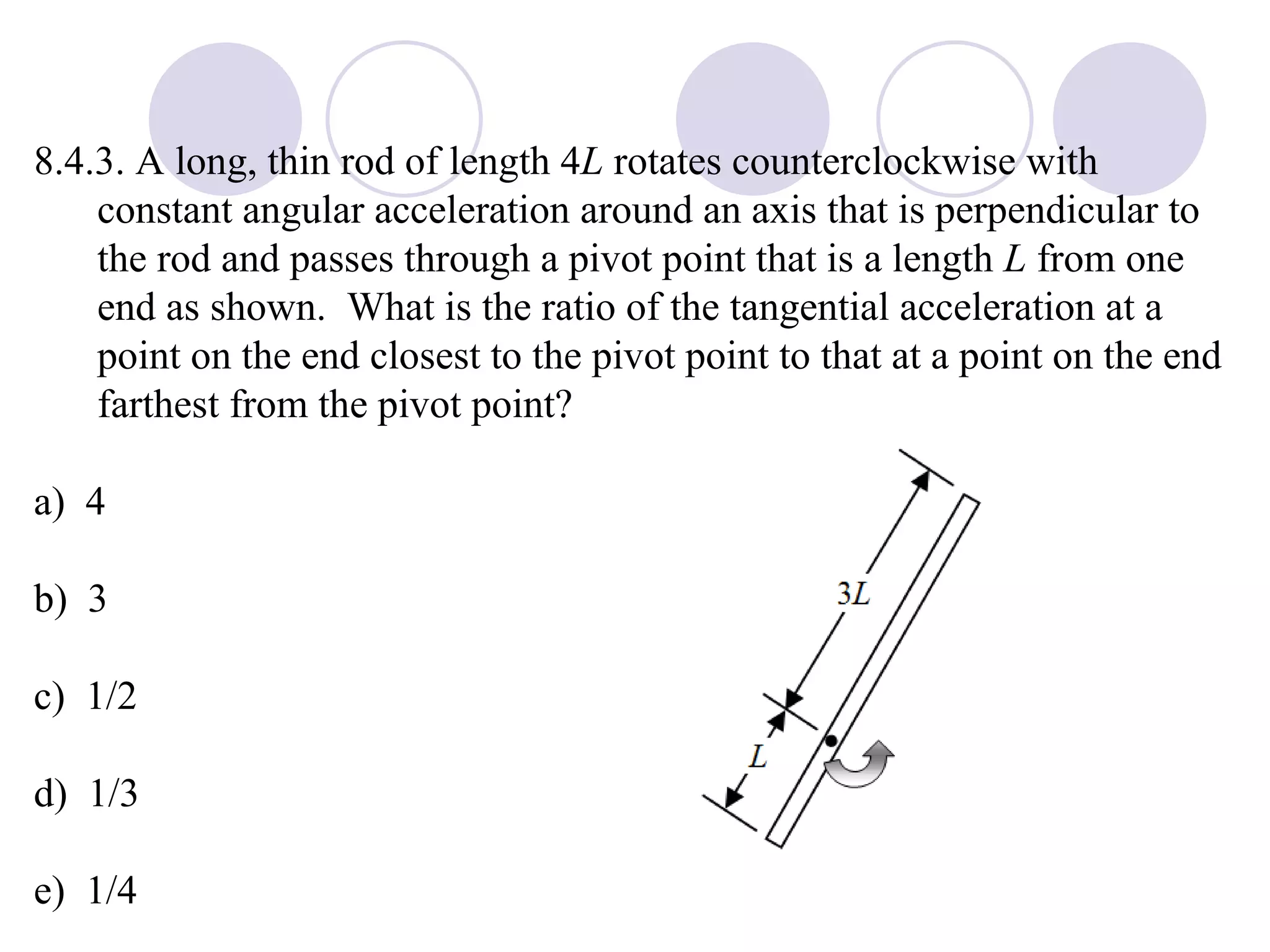
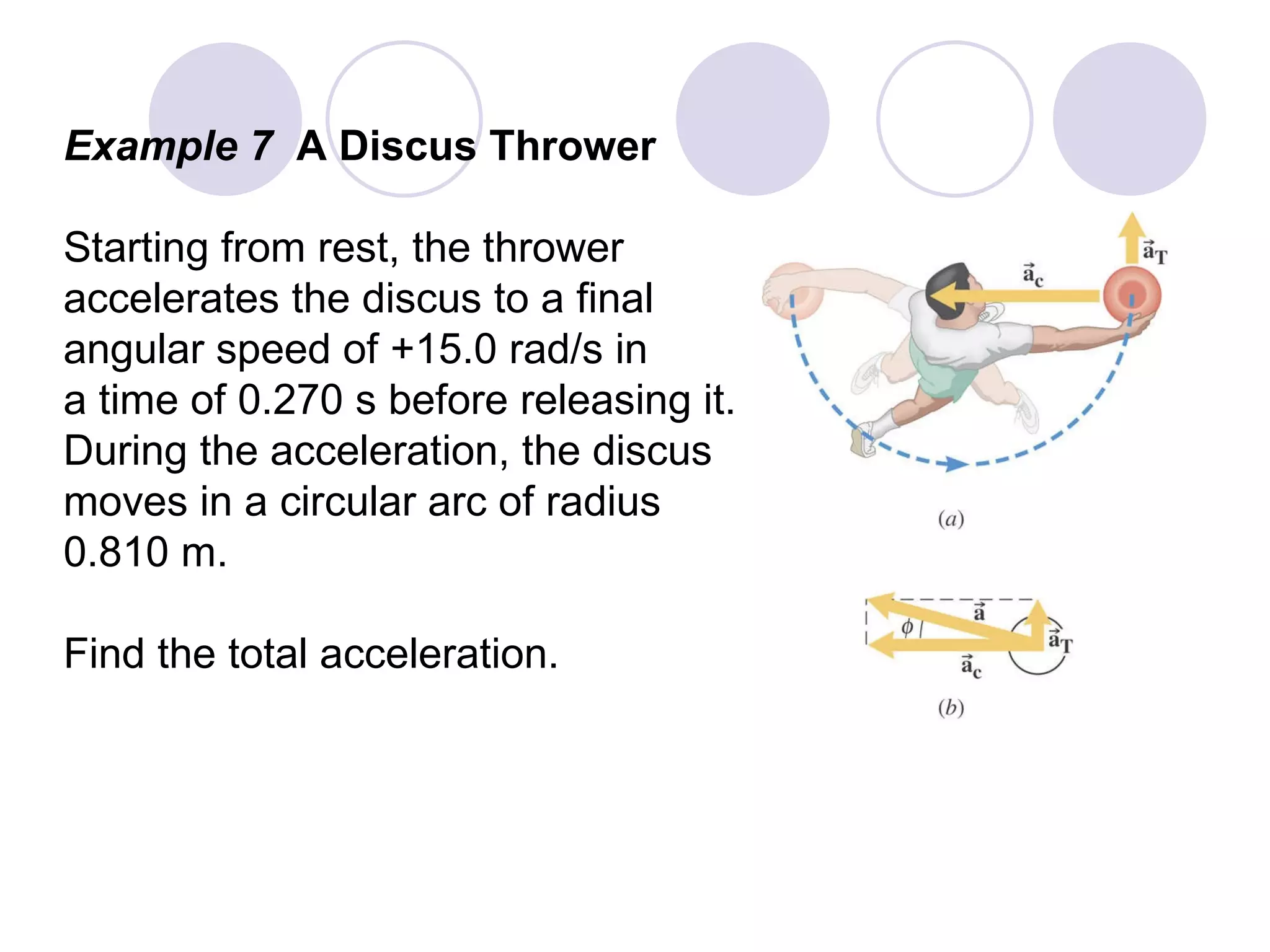
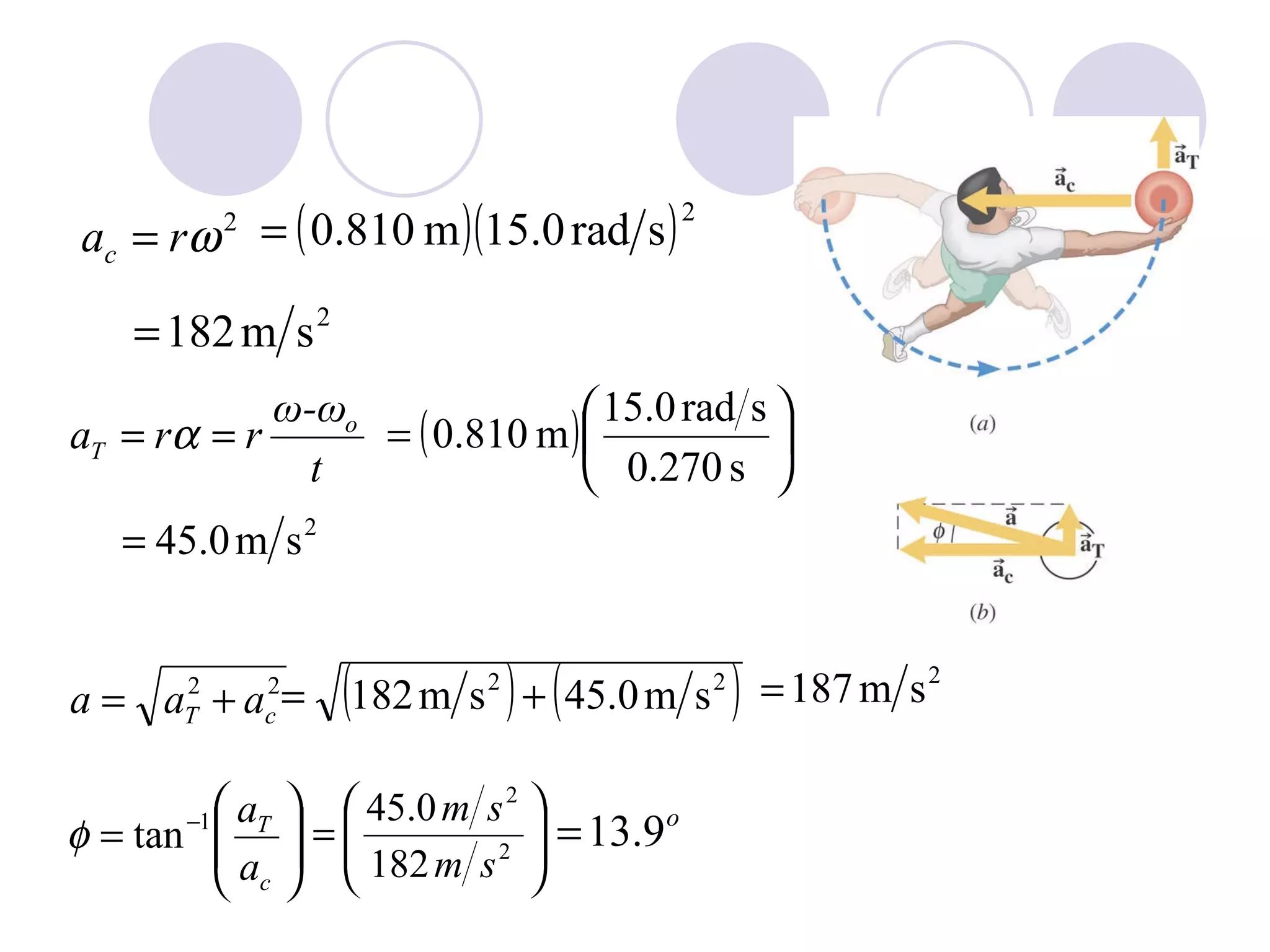
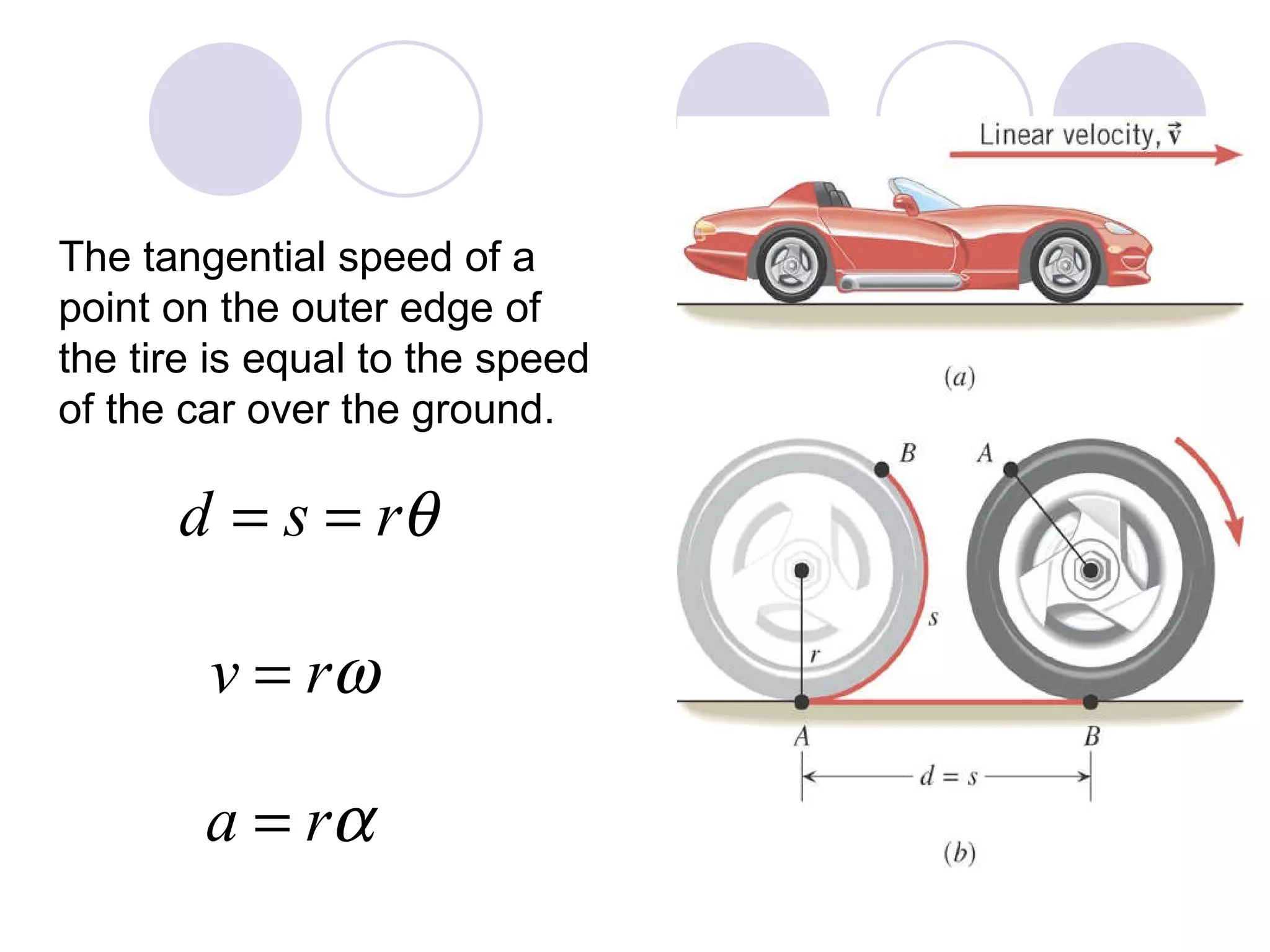
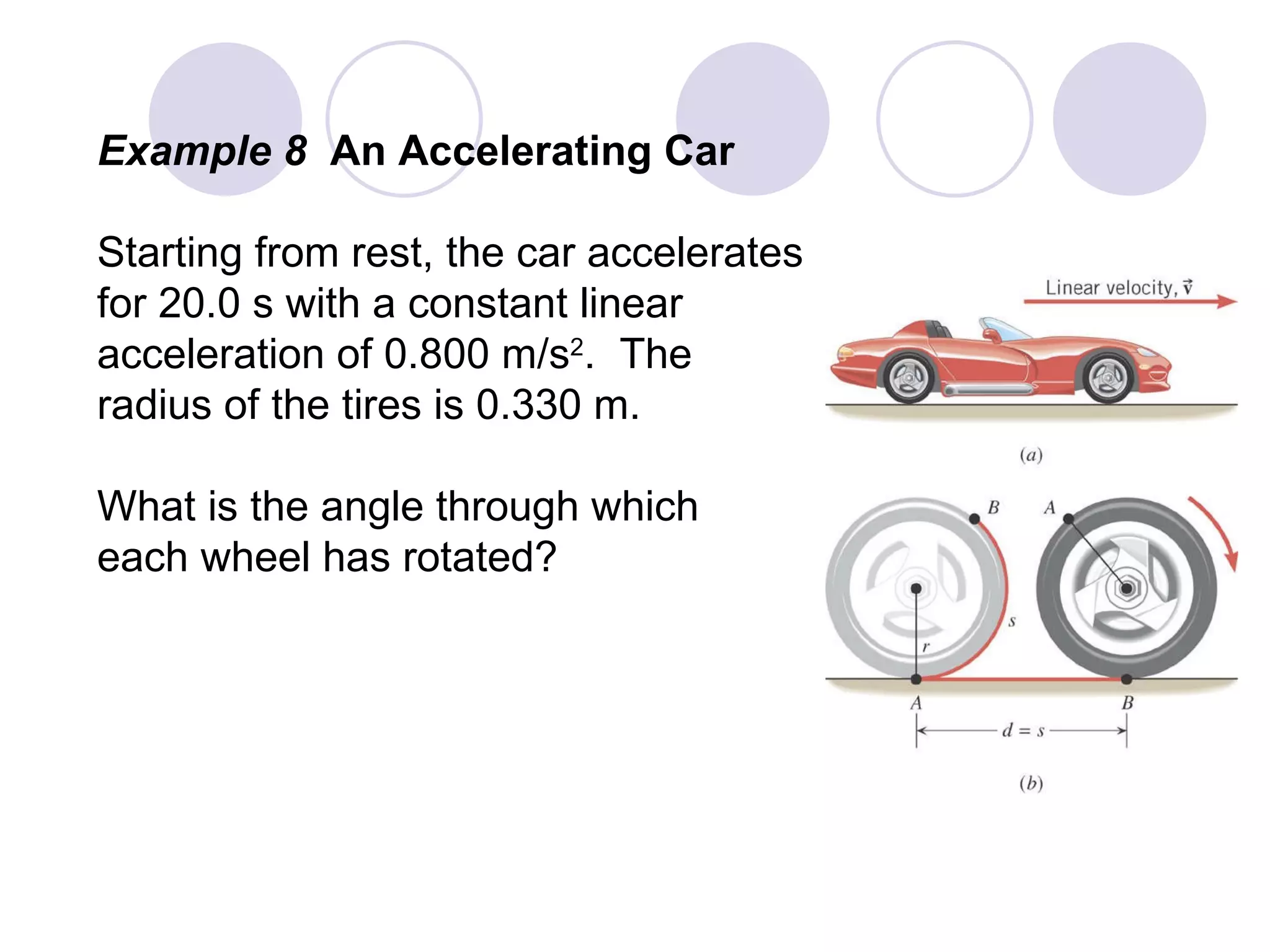
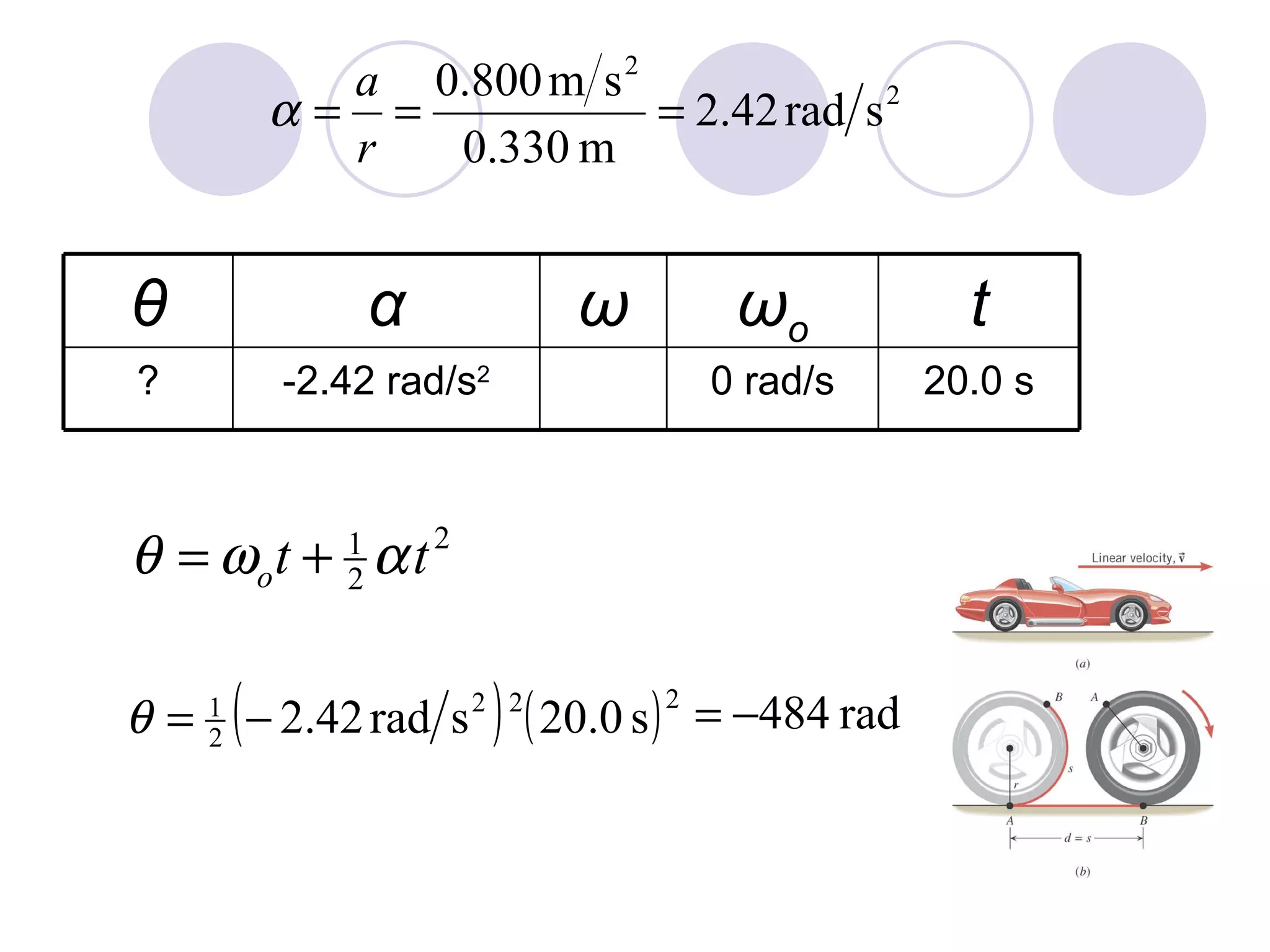
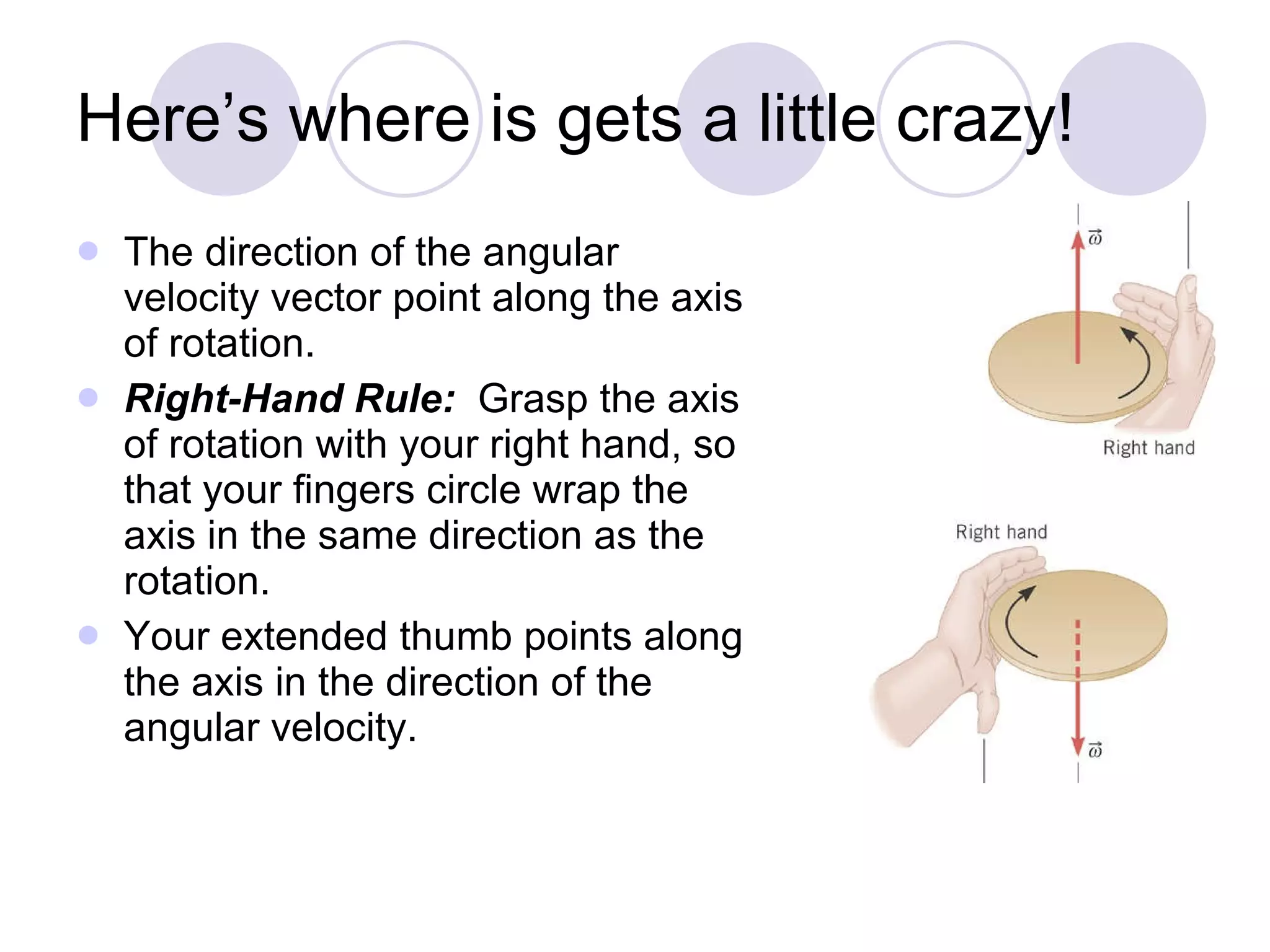
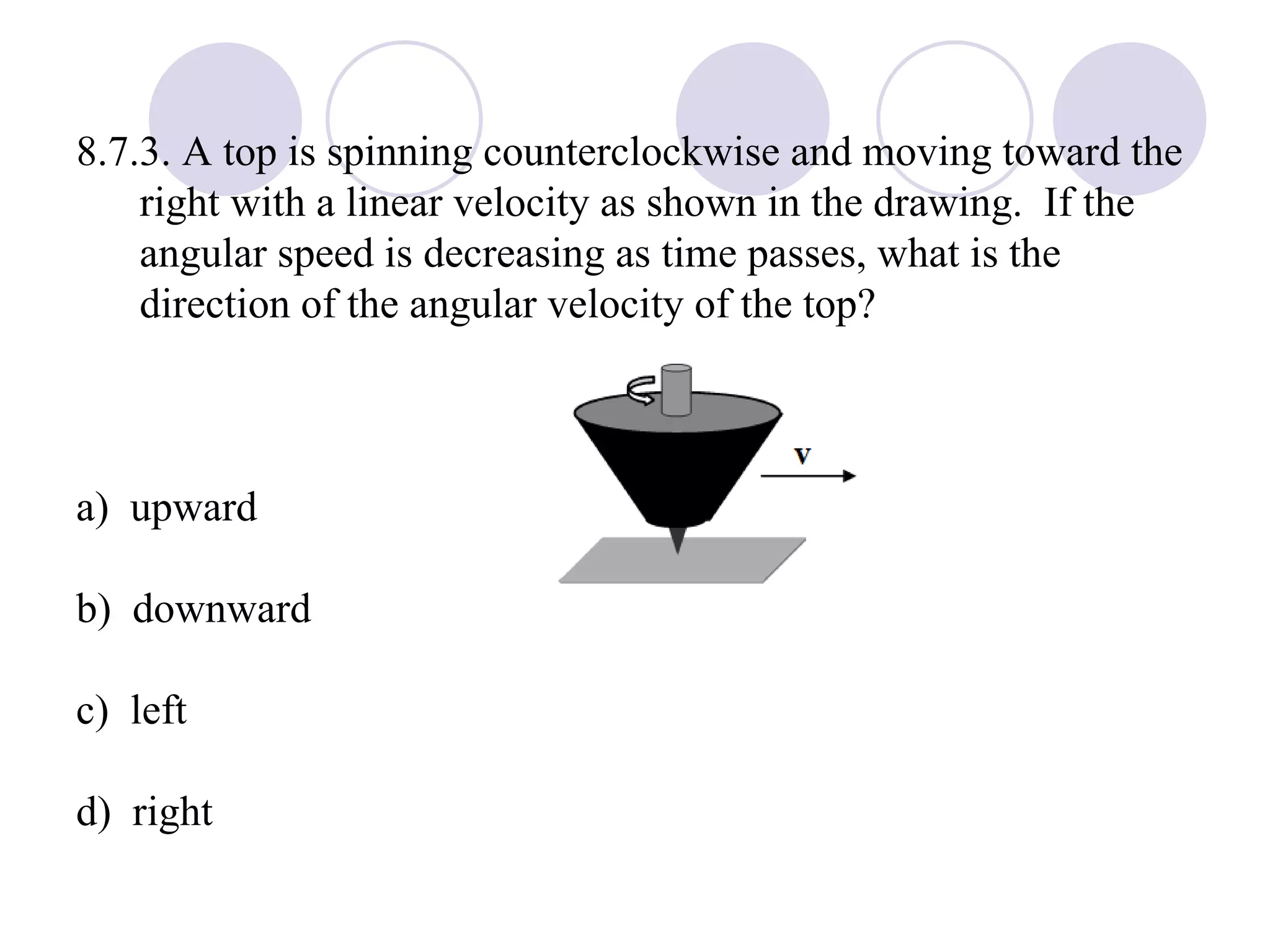
This document provides an overview of key concepts in rotational kinematics covered in Chapter 8, including angular displacement, velocity, and acceleration. It defines these rotational variables and their relationships to linear motion. Examples are given to illustrate calculating angular variables and transforming between rotational and tangential linear motion for objects like rolling wheels or helicopter blades. Formulas for rotational kinematics with constant angular acceleration are also presented.

1. Rotational Kinematics Chapters 8

2. Learning Objectives Objectives for this chapter fall under applications of previous objectives

3. Table Of Contents Rotational Motion and Angular Displacement Angular Velocity and Angular Acceleration The Equations of Rotational Kinematics Angular Variables and Tangential Acceleration Centripetal Acceleration and Tangential Acceleration Rolling Motion The Vector Nature of Angular Variables

4. Chapter 8: Rotational Kinematics Section 1: Rotational Motion and Angular Displacement

5. Describing Rotating Objects As we began to discuss, not all motion is linear. In the simplest kind of rotation, points on a rigid object move on circular paths around an axis of rotation.

6. First there was displacement (d) Need to develop new variables for polar system The angle through which the object rotates is called the Angular displacement.

7. DEFINITION OF ANGULAR DISPLACEMENT When a rigid body rotates about a fixed axis, the angular displacement is the angle swept out by a line passing through any point on the body and intersecting the axis of rotation perpendicularly. By convention, the angular displacement is positive if it is counterclockwise and negative if it is clockwise. SI Unit of Angular Displacement: radian (rad)

8. For a full revolution:

9. Example 1 Adjacent Synchronous Satellites Synchronous satellites are put into an orbit whose radius is 4.23 ×10 7 m. If the angular separation of the two satellites is 2.00 degrees, find the arc length that separates them.

10. 8.1.1. Over the course of a day (twenty-four hours), what is the angular displacement of the second hand of a wrist watch in radians? a) 1440 rad b) 2880 rad c) 4520 rad d) 9050 rad e) 543 000 rad

11. Chapter 8: Rotational Kinematics Section 2: Angular Velocity and Angular Acceleration

12. Next, there was “velocity” How do we describe the rate at which the angular displacement is changing?

13. DEFINITION OF AVERAGE ANGULAR VELOCITY SI Unit of Angular Velocity: radian per second (rad/s)

14. Example 3 Gymnast on a High Bar A gymnast on a high bar swings through two revolutions in a time of 1.90 s. Find the average angular velocity of the gymnast.

15. INSTANTANEOUS ANGULAR VELOCITY Instantaneous Angular speed The magnitude of the instantaneous angular velocity SI Unit of Instantaneous Angular velocity: radian per second (rad/s)

16. Then, there was “acceleration” Changing angular velocity means that an angular acceleration is occurring. DEFINITION OF AVERAGE ANGULAR ACCELERATION SI Unit of Angular acceleration: radian per second per second (rad/s 2 )

17. Example 4 A Jet Revving Its Engines As seen from the front of the engine, the fan blades are rotating with an angular speed of -110 rad/s. As the plane takes off, the angular velocity of the blades reaches -330 rad/s in a time of 14 s. Find the angular acceleration, assuming it to be constant.

18. 8.2.1. The planet Mercury takes only 88 Earth days to orbit the Sun. The orbit is nearly circular, so for this exercise, assume that it is. What is the angular velocity, in radians per second, of Mercury in its orbit around the Sun? a) 8.3 × 10  7 rad/s b) 2.0 × 10  5 rad/s c) 7.3 × 10  4 rad/s d) 7.1 × 10  2 rad/s e) This cannot be determined without knowing the radius of the orbit.

19. 8.2.2. Complete the following statement: For a wheel that turns with constant angular speed, a) each point on its rim moves with constant acceleration. b) the wheel turns through “equal angles in equal times.” c) each point on the rim moves at a constant velocity. d) the angular displacement of a point on the rim is constant. e) all points on the wheel are moving at a constant velocity.

20. Chapter 8: Rotational Kinematics Section 3: The Equations of Rotational Kinematics

21. Making Sense of it All Five kinematic variables displacement initial velocity final velocity elapsed time acceleration  x v o v t a   o  t 

22. The equations of rotational kinematics for constant angular acceleration:

23. Reasoning Strategy Make a drawing. Decide which directions are to be called positive (+) and negative (-). (Counterclockwise default +) Write down the values that are given for any of the five kinematic variables. Verify that the information contains values for at least three of the five kinematic variables. Select the appropriate equation. When the motion is divided into segments, remember that the final angular velocity of one segment is the initial velocity for the next. Keep in mind that there may be two possible answers to a kinematics problem.

24. Example 5 Blending with a Blender The blades are whirling with an angular velocity of +375 rad/s when the “puree” button is pushed in. When the “blend” button is pushed, the blades accelerate and reach a greater angular velocity after the blades have rotated through an angular displacement of +44.0 rad. The angular acceleration has a constant value of +1740 rad/s 2 . Find the final angular velocity of the blades.

25. +375 rad/s ? +1740 rad/s 2 +44.0 rad t ω o ω α  θ

26. 8.3.1. The propeller of an airplane is at rest when the pilot starts the engine; and its angular acceleration is a constant value. Two seconds later, the propeller is rotating at 10  rad/s. Through how many revolutions has the propeller rotated through during the first two seconds? a) 300 b) 50 c) 20 d) 10 e) 5

27. 8.3.2. A ball is spinning about an axis that passes through its center with a constant angular acceleration of  rad/s 2 . During a time interval from t 1 to t 2 , the angular displacement of the ball is  radians. At time t 2 , the angular velocity of the ball is 2  rad/s. What is the ball’s angular velocity at time t 1 ? a) 6.28 rad/s b) 3.14 rad/s c) 2.22 rad/s d) 1.00 rad/s e) zero rad/s

28. Chapter 8: Rotational Kinematics Section 4: Angular Variables and Tangential Acceleration

29. Relating to the “Worlds” Sometimes it’s easier to solve the problem with “rotational” kinematics, sometimes with “translational” What we will now look at is relating or transforming from one system to the other. How does the “linear” or rather tangential speed relate to the angular speed?

31. Example 6 A Helicopter Blade A helicopter blade has an angular speed of 6.50 rev/s and an angular acceleration of 1.30 rev/s 2 . For point 1 on the blade, find the magnitude of (a) the tangential speed and (b) the tangential acceleration.

32. 8.4.1. The Earth, which has an equatorial radius of 6380 km, makes one revolution on its axis every 23.93 hours. What is the tangential speed of Nairobi, Kenya, a city near the equator? a) 37.0 m/s b) 74.0 m/s c) 148 m/s d) 232 m/s e) 465 m/s

33. 8.4.2. The original Ferris wheel had a radius of 38 m and completed a full revolution (2  radians) every two minutes when operating at its maximum speed. If the wheel were uniformly slowed from its maximum speed to a stop in 35 seconds, what would be the magnitude of the instantaneous tangential speed at the outer rim of the wheel 15 seconds after it begins its deceleration? a) 0.295 m/s b) 1.12 m/s c) 1.50 m/s d) 1.77 m/s e) 2.03 m/s

34. 8.4.3. A long, thin rod of length 4 L rotates counterclockwise with constant angular acceleration around an axis that is perpendicular to the rod and passes through a pivot point that is a length L from one end as shown. What is the ratio of the tangential acceleration at a point on the end closest to the pivot point to that at a point on the end farthest from the pivot point? a) 4 b) 3 c) 1/2 d) 1/3 e) 1/4

35. 8.4.4. A long, thin rod of length 4 L rotates counterclockwise with constant angular acceleration around an axis that is perpendicular to the rod and passes through a pivot point that is a length L from one end as shown. What is the ratio of the tangential speed (at any instant) at a point on the end closest to the pivot point to that at a point on the end farthest from the pivot point? a) 1/4 b) 1/3 c) 1/2 d) 3 e) 4

36. Chapter 8: Rotational Kinematics Section 5: Centripetal Acceleration and Tangential Acceleration

37. Relationship to Circular Motion How do we relate rotational kinematics to Uniform Circular Motion (Ch 5) Even if “tangential” speed is constant, there is still an acceleration.

38. Tangential Acceleration? From Ch 5, we define the axes as polar co-ordinates not Cartesian. (r,  ) not (x,y) Since they are perpendicular, we can treat each axis independently Therefore, total acceleration would be vector sum of a c plus a T

39. Example 7 A Discus Thrower Starting from rest, the thrower accelerates the discus to a final angular speed of +15.0 rad/s in a time of 0.270 s before releasing it. During the acceleration, the discus moves in a circular arc of radius 0.810 m. Find the total acceleration.

41. 8.5.1. An airplane starts from rest at the end of a runway and begins accelerating. The tires of the plane are rotating with an angular velocity that is uniformly increasing with time. On one of the tires, Point A is located on the part of the tire in contact with the runway surface and point B is located halfway between Point A and the axis of rotation. Which one of the following statements is true concerning this situation? a) Both points have the same tangential acceleration. b) Both points have the same centripetal acceleration. c) Both points have the same instantaneous angular velocity. d) The angular velocity at point A is greater than that of point B. e) Each second, point A turns through a greater angle than point B.

42. 8.5.2. A wheel starts from rest and rotates with a constant angular acceleration. What is the ratio of the instantaneous tangential acceleration at point A located a distance 2 r to that at point B located at r, where the radius of the wheel is R = 2 r ? a) 0.25 b) 0.50 c) 1.0 d) 2.0 e) 4.0

43. Chapter 8: Rotational Kinematics Section 6: Rolling Motion

44. Rolling Motion A rolling object is a common example of when you would need to be able to transform from one coordinate system to the other. Usually a “rolling” object will not be slipping on the surface.

45. The tangential speed of a point on the outer edge of the tire is equal to the speed of the car over the ground.

46. Example 8 An Accelerating Car Starting from rest, the car accelerates for 20.0 s with a constant linear acceleration of 0.800 m/s 2 . The radius of the tires is 0.330 m. What is the angle through which each wheel has rotated?

47. 20.0 s 0 rad/s -2.42 rad/s 2 ? t ω o ω α θ

48. 8.6.1. The wheels of a bicycle have a radius of r meters. The bicycle is traveling along a level road at a constant speed v m/s. Which one of the following expressions may be used to determine the angular speed, in rev/min, of the wheels? a) b) c) d) e)

49. 8.6.2. Josh is painting yellow stripes on a road using a paint roller. To roll the paint roller along the road, Josh applies a force of 15 N at an angle of 45  with respect to the road. The mass of the roller is 2.5 kg; and its radius is 4.0 cm. Ignoring the mass of the handle of the roller, what is the magnitude of the tangential acceleration of the roller? a) 4.2 m/s 2 b) 6.0 m/s 2 c) 15 m/s 2 d) 110 m/s 2 e) 150 m/s 2

50. 8.6.3. Which one of the following statements concerning a wheel undergoing rolling motion is true? a) The angular acceleration of the wheel must be zero m/s 2 . b) The tangential velocity is the same for all points on the wheel. c) The linear velocity for all points on the rim of the wheel is non-zero. d) The tangential velocity is the same for all points on the rim of the wheel. e) There is no slipping at the point where the wheel touches the surface on which it is rolling.

51. 8.6.4. A circular hoop rolls without slipping on a flat horizontal surface. Which one of the following is necessarily true? a) All points on the rim of the hoop have the same speed. b) All points on the rim of the hoop have the same velocity. c) Every point on the rim of the wheel has a different velocity. d) All points on the rim of the hoop have acceleration vectors that are tangent to the hoop. e) All points on the rim of the hoop have acceleration vectors that point toward the center of the hoop.

52. 8.6.5. A bicycle wheel of radius 0.70 m is turning at an angular speed of 6.3 rad/s as it rolls on a horizontal surface without slipping. What is the linear speed of the wheel? a) 1.4 m/s b) 28 m/s c) 0.11 m/s d) 4.4 m/s e) 9.1 m/s

53. Chapter 8: Rotational Kinematics Section 7: The Vector Nature of Angular Variables

54. Here’s where is gets a little crazy! The direction of the angular velocity vector point along the axis of rotation. Right-Hand Rule: Grasp the axis of rotation with your right hand, so that your fingers circle wrap the axis in the same direction as the rotation. Your extended thumb points along the axis in the direction of the angular velocity.

55. 8.7.1. A packaged roll of paper towels falls from a shelf in a grocery store and rolls due south without slipping. What is the direction of the paper towels’ angular velocity? a) north b) east c) south d) west e) down

56. 8.7.2. A packaged roll of paper towels falls from a shelf in a grocery store and rolls due south without slipping. As its linear speed slows, what are the directions of the paper towels’ angular velocity and angular acceleration? a) east, east b) west, east c) south, north d) east, west e) west, west

57. 8.7.3. A top is spinning counterclockwise and moving toward the right with a linear velocity as shown in the drawing. If the angular speed is decreasing as time passes, what is the direction of the angular velocity of the top? a) upward b) downward c) left d) right

58. 8.7.4. A truck and trailer have 18 wheels. If the direction of the angular velocity vectors of the 18 wheels point 30  north of east, in what direction is the truck traveling? a) 30° east of south b) 30° west of north c) 30° north of east d) 30° south of west e) 30° south of east

59. 8.7.5. A girl is sitting on the edge of a merry-go-round at a playground as shown. Looking down from above, the merry-go-round is rotating clockwise. What is the direction of the girl’s angular velocity? a) upward b) downward c) left d) right e) There is no direction since it is the merry go round that has the angular velocity.

60. END