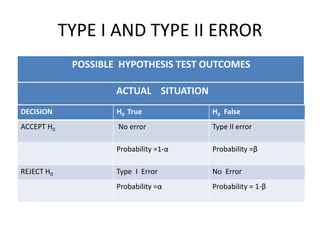
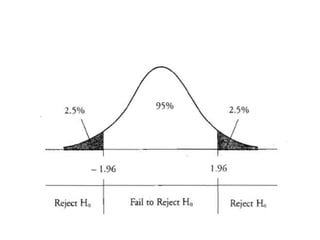
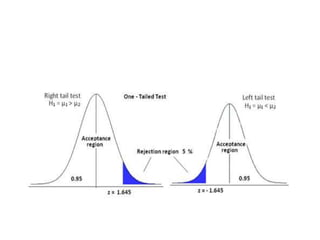
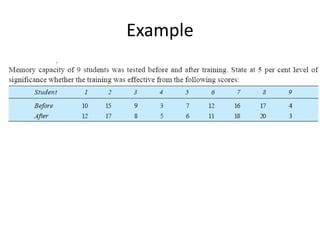
This document summarizes a presentation on hypothesis testing. It defines key concepts like the null and alternative hypotheses, type I and type II errors, and one-tailed and two-tailed tests. It then outlines the procedure for hypothesis testing, including setting hypotheses, selecting a significance level, calculating test statistics, and determining whether to reject the null hypothesis. Specific hypothesis tests are described, like paired t-tests for comparing two related samples and tests of proportions. Limitations of hypothesis testing are noted, such as that results are probabilistic and small samples impact reliability.

1. Presentation
on
Testing of Hypothesis
By:
Ankit Dubey
Chintan H.Trivedi

2. • Basics of Hypothesis
• Procedure of Hypothesis Testing
• Testing Of Hypothesis for Comparing two
related samples
• Hypothesis testing of Proportion
• Limitations of Test of Hypothesis

3. HYPOTHESIS
• For a researcher hypothesis is a formal question
that he intends to resolve.
• Hypothesis may be defined as a proposition or a
set of proposition set forth as an explanation for
the occurrence of some specified group of
phenomena.
• Example: vehicle A performs better than vehicle B

4. NULL HYPOTHESIS AND ALTERNATIVE
HYPOTHESIS
• Null hypothesis: when population mean is
equal to hypothesis mean
• Alternative hypothesis : the hypothesis which
is accepted when null hypothesis fails
• A set of alternatives to null hypothesis is
called alternative hypothesis
• Null hypothesis always include = to sign
• Alternative hypothesis may include any of the
inequality signs

5. ALTERNATIVE HYPOTHESIS
ALTERNATIVE
HYPOTHESIS
MEANING
H0: μ ≠ μ0 Population mean is not equal to hypothesis
mean
H1 :μ>μ0 Population mean is greater than hypothesis
mean
H1 :μ<μ0 Population mean is greater than hypothesis
mean

6. TYPE I AND TYPE II ERROR
POSSIBLE HYPOTHESIS TEST OUTCOMES
ACTUAL SITUATION
DECISION H0 True H0 False
ACCEPT H0 No error Type II error
Probability =1-α Probability =β
REJECT H0 Type I Error No Error
Probability =α Probability = 1-β

7. CRITICAL VALUE
It divides area under probability curve into two
regions critical and acceptance regions
In two tailed test we wish to test H0 : μ =μ0
against H1 : μ≠ μ0 we have two critical values
which divides probability curve into two
regions

8. Level of significance
• Denoted by α is the probability of Type 1 error.
• It is usually 5% which should be chosen with
great care thought and reason.
• If level of significance is 5% then researcher is
willing to take as much as 5% percent risk of
rejecting null hypothesis if it is true.
• Maximum Value of probability of rejecting H0
when it is true.
• Determined usually in advance prior to testing
of hypothesis.

9. Two Tailed And One Tailed Test
• Testing three types of Hypothesis given by:
• H0 :μ = μ0 Against H1 :μ ≠ μ0 (two tailed test)
• H0 :μ ≤ μ0 Against H1 :μ > μ0 (Right tailed test)
• H0 :μ ≥ μ0 Against H1 :μ < μ0 (Left tailed test)

12. PROCEDURE FOR HYPOTHESIS TESTING
• It is used to test validity of hypothesis
• Setting up the hypothesis: Formal statement
of null and alternative hypothesis
• Selecting significance level:pre determined
level of significance based on sample size,
variability of measurements with in sample
• Test statistic: to obtain value of mean
,variance etc on basis of distribution selected

13. PROCEDURE FOR HYPOTHESIS TESTING
• Critical value: depends on type of
distribution, level of significance, type of test
• Decision: compare the value of test statistic
and critical value
• we reject null hypothesis when
• Test statistic value< lower than critical
value>upper critical value
• Value of test statistic > critical value
• Value of test statistic < critical value

14. HYPOTHESIS TESTING FOR
COMPARING TWO RELATED SAMPLES
• Paired t-test is a way to test for comparing two
related samples,
• For a paired t-test, observations in the two
samples collected in the form matched pairs
• “each observation in the one sample must be
paired with an observation in the other sample in
such a manner that these observations are
somehow “matched” or related, in an attempt to
eliminate extraneous factors which are not of
interest in test.”

15. • Such a test is generally considered appropriate in
a before-and-after-treatment study.
• Testing a group of certain students before and
after training in order to know whether the
training is effective, in which situation we may
use paired t-test.
• To apply this test, :
a. Work out the difference score for each
matched pair
b. Find out the average of such differences, D
c. Sample variance of the difference score.

16. • If the values from the two matched samples
are denoted as Xi and Yi and the differences
by Di (Di = Xi – Yi), then the mean of the
differences i.e.,
• And Variance of the differences:

17. • To work out the test statistic (t):
Where

18. Example

19. • Formulation of Null And Alternate Hypothesis
• Work out Test Statistic

20. • Standard deviation of differences:

21. HYPOTHESIS TESTING OF PROPORTION
• Population is divided into exclusive and
exhaustive tests based on certain attribute
• One class having attribute and other not
• Important parameter is proportion of
population having that attribute
H0 :π≤ π0, H1 : π> π0 (Right or Upper tail test)
H0 : π≥ π0 , H1 π< π0 (left or lower tail test)
H0 : π= π0 , H1 : π≠ π0 (two upper tail test)

22. • Test statistic for this test
Z = p - π0
√ π0 (1- π0 )/n
p=sample proportion

23. HYPOTHESIS TESTING OF TWO
PROPORTION
• Two population proportions are compared
• Two population proportion are obtained from
two different samples
• Hence following hypothesis is tested
H0 : π1 = π2 against H1 : π1 ≠ π2
H0 : π1 = π2 against H1 : π1 > π2 or H0 π1 ≤ π2
Against H1 : π1 > π2
H0 : π1 = π2 Against H1 π1 < π2 or π1 ≥ π2 Against H1
π1 < π2

24. EXAMPLE
Q) A sample survey indicates that out of 3232 births,
1705 were boys and the rest were girls. Do these
figures confirm the hypothesis that the sex ratio is
50 : 50? Test at 5 per cent level of significance.
Solution: Starting from the null hypothesis that the sex
ratio is 50 : 50 we may write:

27. Hypothesis testing for Variance
1. H0 :σ2 = σ0
2 , H1 : σ2 ≠ σ0
2 (two tailed test)
2. H0 :σ2 = σ0
2 , H1 : σ2 > σ0
2 (right tailed test)
3. H0 :σ2 = σ0
2 , H1 : σ2 < σ0
2 (left tailed test)

28. Limitations of Test of Hypothesis
• Important limitations are as follows:
• Testing is not decision-making itself; the tests are only
useful aids for decision-making.
• “proper interpretation of statistical evidence is
important to intelligent decisions.”
• Test do not explain the reasons as to why does the
difference exist, viz. between the means of the two
samples.
• They simply indicate whether the difference is due to
fluctuations of sampling or because of other reasons
• The tests do not tell us the reasons causing the
difference.

29. • Results of significance tests are based on probabilities
and as such cannot be expressed with full certainty.
• Statistical inferences based on the significance tests
cannot be said to be entirely correct evidences
concerning the truth of the hypotheses.
• This is specially so in case of small samples where the
probability of drawing erring inferences happens to be
generally higher.
• For greater reliability, the size of samples be sufficiently
enlarged.

30. • All these limitations suggest that in problems
of statistical significance, the inference
techniques (or the tests) must be combined
with adequate knowledge of the subject-
matter along with the ability of good
judgement.

31. Thank You!