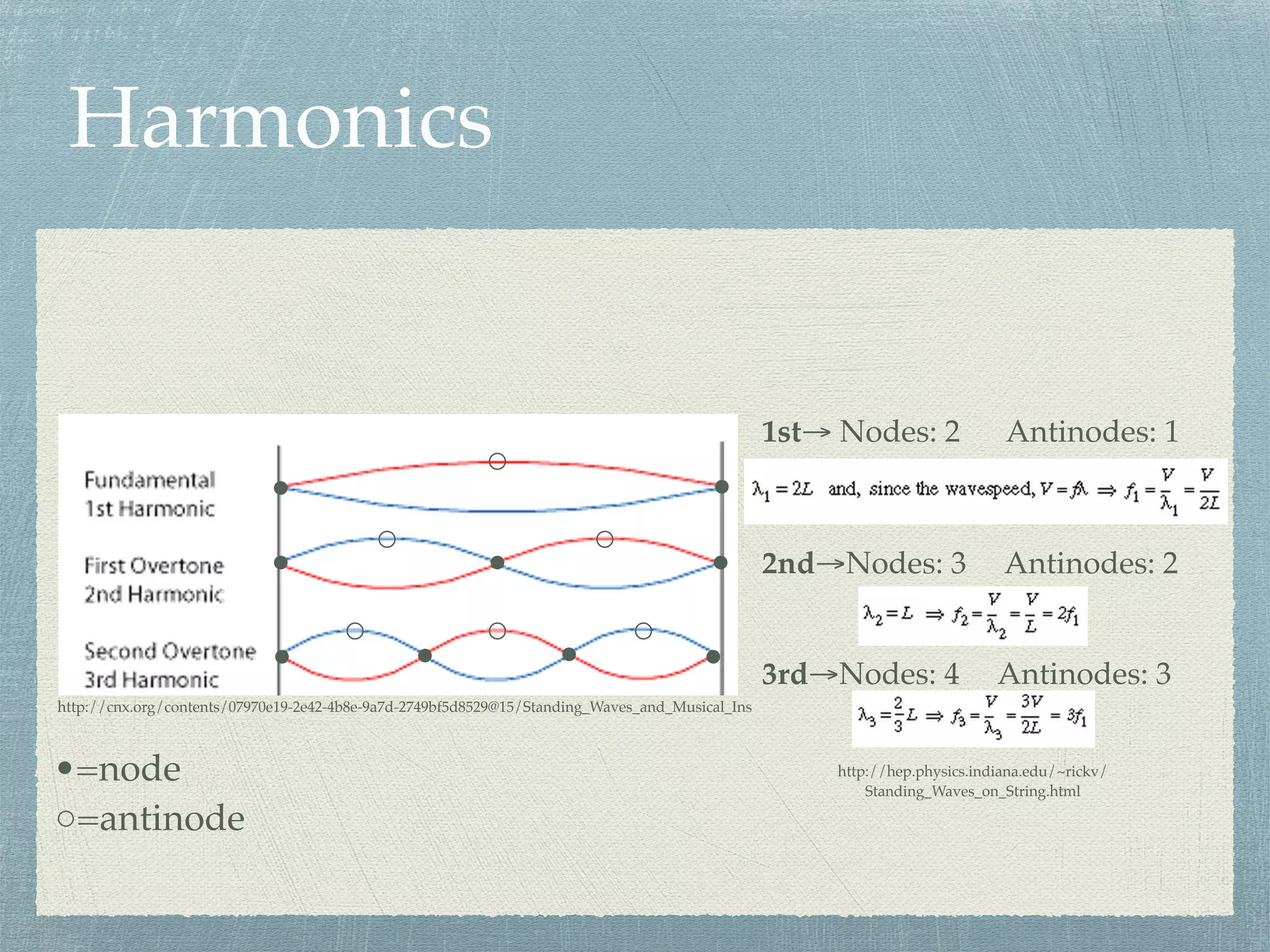
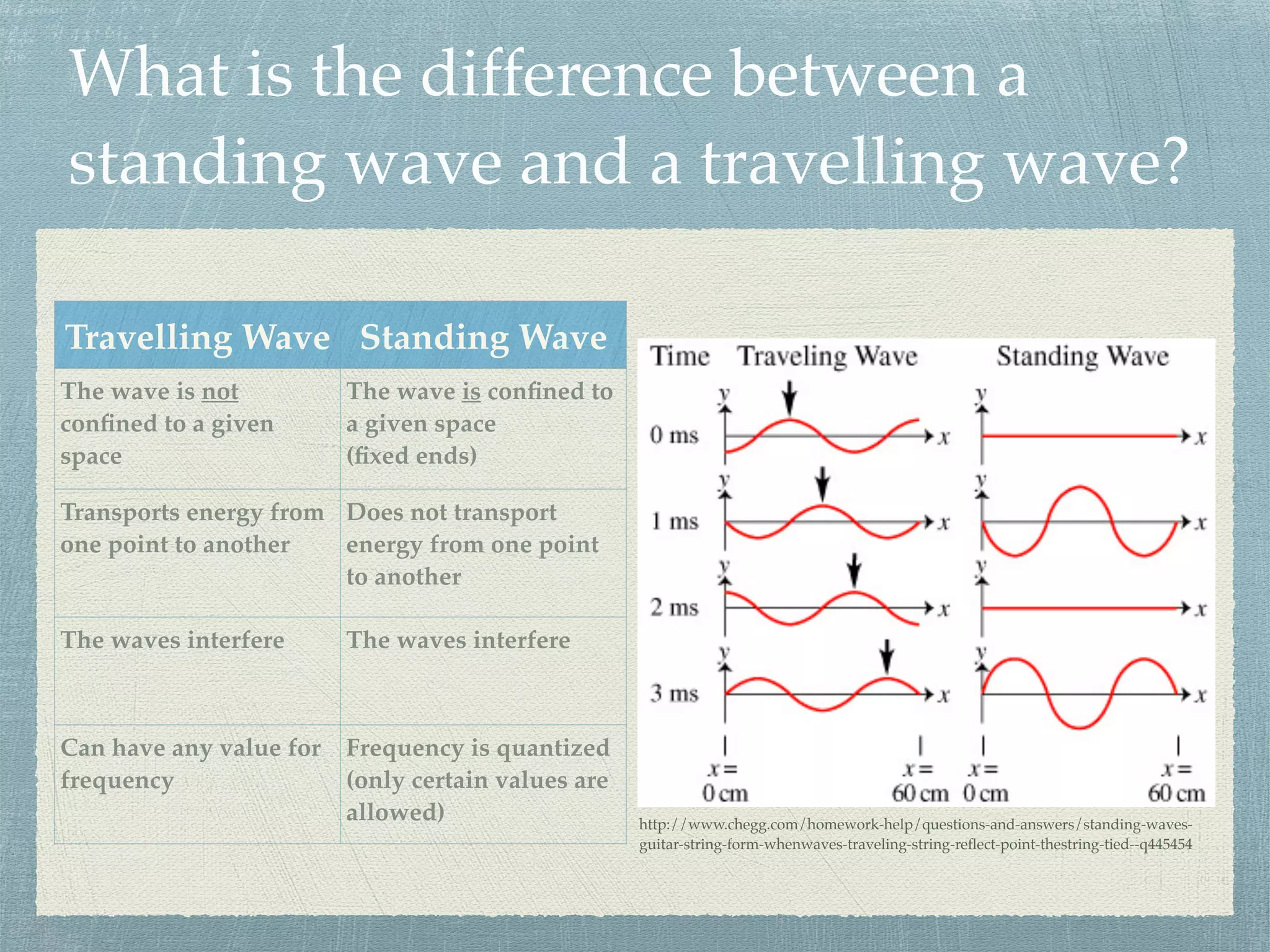
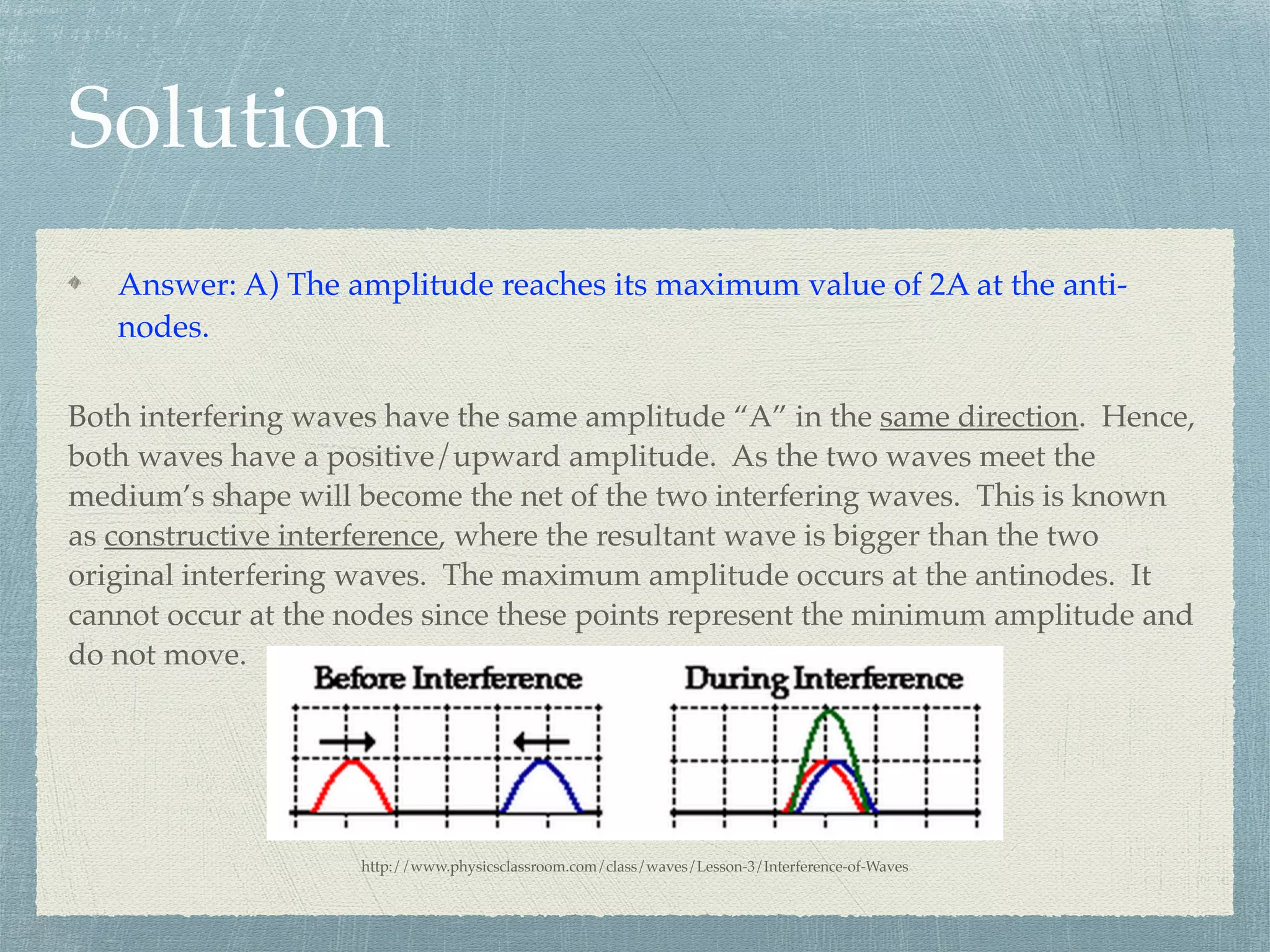
The document provides an overview of standing waves on a string, detailing key concepts such as nodes, antinodes, incident waves, and harmonics. It explains the differences between standing and traveling waves, supported by equations and examples for calculating frequency, wavelength, and wave speed. Additionally, it addresses how amplitude is affected by interference and includes resources for further understanding.

1. Standing Waves on a String
By: Aysha Allard Brown
http://pixshark.com/standing-waves-on-a-string.htm

2. Definitions
Node: a point on a standing wave along a string that does not move
ex. the end points of a string
Antinode: the region of maximum amplitude between two adjacent nodes in a
standing wave along a string
Incident Wave: a wave that strikes a boundary, where it is then reflected/flipped
Reflected Wave: the reflected/flipped incident wave (180°)
λ: wavelength (m)
L: length of the string (m)
http://www.clemson.edu/ces/phoenix/labs/224/standwave/

3. In a standing wave, the string is held fixed at the end points
Some specific points do not move (nodes) and the points
between them vibrate (antinodes)
The maximum amplitude of the wave corresponds to the
antinode
The minimum amplitude of the wave corresponds to the node
A standing wave is a result of two similar waves travelling in
opposite directions
What is a standing wave?

4. What is a standing wave?
Different frequencies are associated with different wave
patterns for standing waves
These frequencies along with their corresponding
patterns are referred to as harmonics
A harmonic is an integer which is a multiple of the
fundamental frequency (the lowest frequency→ when
the number of nodes=2)

5. Harmonics
1st→ Nodes: 2 Antinodes: 1
2nd→Nodes: 3 Antinodes: 2
3rd→Nodes: 4 Antinodes: 3
•=node
•
• •
•
•
•
• • •
○=antinode
○
○
○
○
○ ○
http://cnx.org/contents/07970e19-2e42-4b8e-9a7d-2749bf5d8529@15/Standing_Waves_and_Musical_Ins
http://hep.physics.indiana.edu/~rickv/
Standing_Waves_on_String.html

6. What is the difference between a
standing wave and a travelling wave?
Travelling Wave Standing Wave
The wave is not
confined to a given
space
The wave is confined to
a given space
(fixed ends)
Transports energy from
one point to another
Does not transport
energy from one point
to another
The waves interfere The waves interfere
Can have any value for
frequency
Frequency is quantized
(only certain values are
allowed) http://www.chegg.com/homework-help/questions-and-answers/standing-waves-
guitar-string-form-whenwaves-traveling-string-reflect-point-thestring-tied--q445454

7. Equations
1) T- tension force (N)
m- mass of string (kg)
L- length of string (m)
f- frequency (Hz)
http://hyperphysics.phy-astr.gsu.edu/hbase/waves/string.html

8. Equations
2) n- harmonic number
(# of antinodes)
λ- wavelength (m)
L- length of string (m)
http://www.physicsclassroom.com/class/waves/Lesson-4/Mathematics-of-Standing-Waves

9. Question #1
A string is 5.0 meters long and is vibrating at
the 3rd harmonic. The string vibrates up and
down with 48 complete vibrational cycles in
20 seconds. Determine the frequency, period,
wavelength and speed for this wave.

10. Solution (pt. 1)
1) Determine the frequency
The frequency refers to how often a point on the string goes back-and-forth
(hence the number of cycles per unit time).
Therefore, f = (48 cycles) / (20 seconds) = 2.4 Hz
2) Determine the period
The period is referring to the time needed for one complete cycle of vibration to
pass a given point. The period and frequency share a reciprocal relationship so
therefore,
T= 1 / f
T = 1 / (2.4 Hz) = 0.417 seconds

11. Solution (pt. 2)
3) Determine the wavelength
The wavelength for the 3rd harmonic is represented by λ=2/3*L. The length of
the string is given in the question, 5.0m.
Therefore, λ = 2/3 * (5.0m) = 10/3m = 3.3m
4) Determine the wave speed
Since we calculated the frequency and wavelength above, we can now find the
wave speed by using the following formula:
v = λf = (3.3m)(2.4Hz) = 7.9 m/s

12. Question #2
Which statement is CORRECT about the amplitude of a
standing wave created from the interference of two waves, each
with amplitude ‘A'?
A. The amplitude reaches its maximum value of 2A at the anti-
nodes.
B. The amplitude reaches its maximum value of A at the nodes.
C. The amplitude reaches its maximum value of A at the anti-
nodes.
D. The amplitude reaches its maximum value of 2A at the nodes.

13. Solution
Answer: A) The amplitude reaches its maximum value of 2A at the anti-
nodes.
Both interfering waves have the same amplitude “A” in the same direction. Hence,
both waves have a positive/upward amplitude. As the two waves meet the
medium’s shape will become the net of the two interfering waves. This is known
as constructive interference, where the resultant wave is bigger than the two
original interfering waves. The maximum amplitude occurs at the antinodes. It
cannot occur at the nodes since these points represent the minimum amplitude and
do not move.
http://www.physicsclassroom.com/class/waves/Lesson-3/Interference-of-Waves

14. YouTube Videos
Standing Waves: Demo
https://www.youtube.com/watch?v=-gr7KmTOrx0
Standing Waves: Calculations
https://www.youtube.com/watch?v=QcoQvzNQp6Q

15. Thank you.

16. Bibliography
http://hyperphysics.phy-astr.gsu.edu/hbase/waves/string.html
http://www.physicsclassroom.com/class/sound/Lesson-4/Standing-Wave-
Patterns
http://hep.physics.indiana.edu/~rickv/Standing_Waves_on_String.html
http://www.physicsclassroom.com/class/waves/Lesson-4/Harmonics-and-
Patterns
http://astarmathsandphysics.com/a-level-physics-notes/waves-and-
oscillations/a-level-physics-notes-the-difference-between-standing-waves-
and-travelling-waves.html