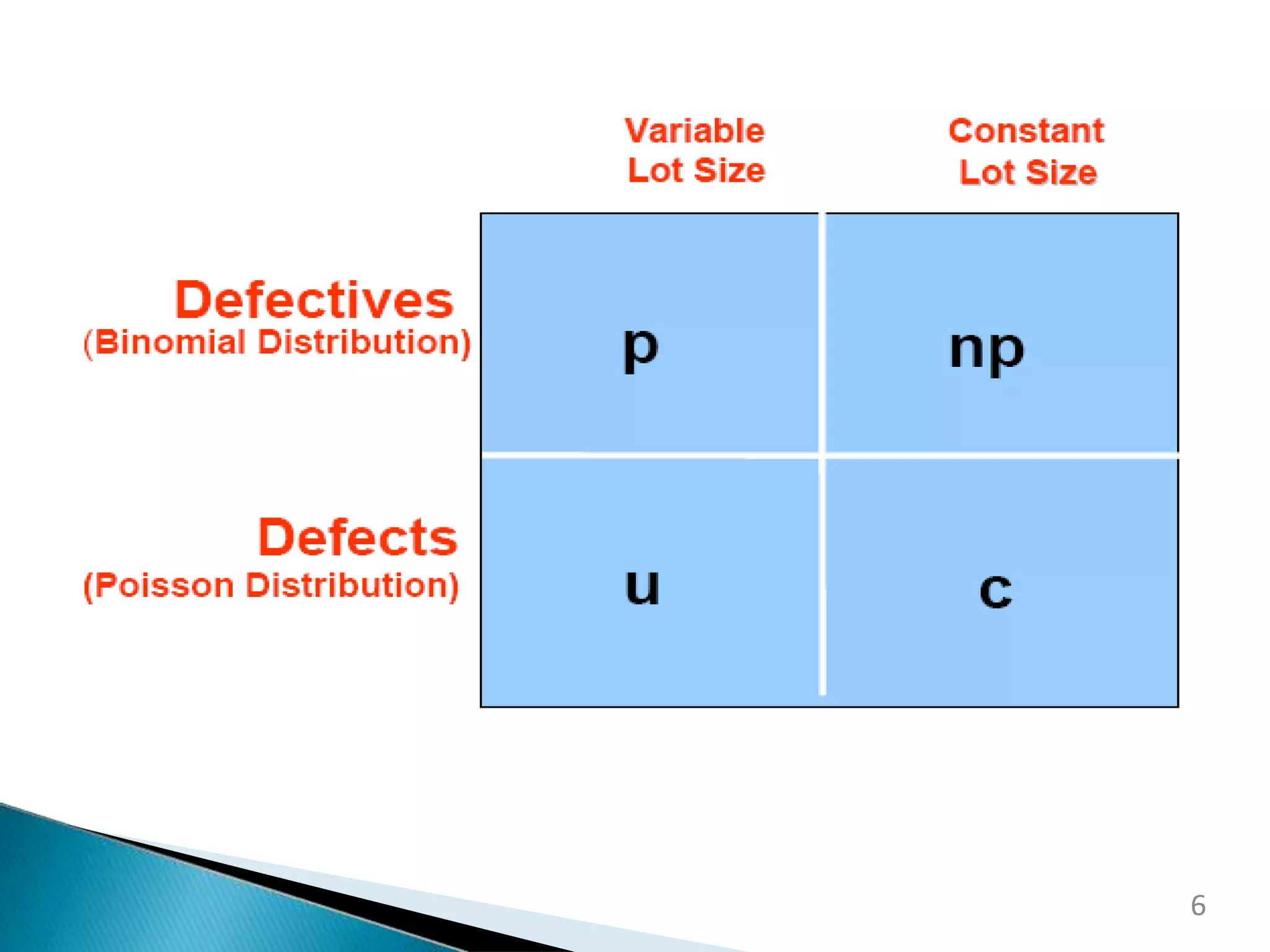
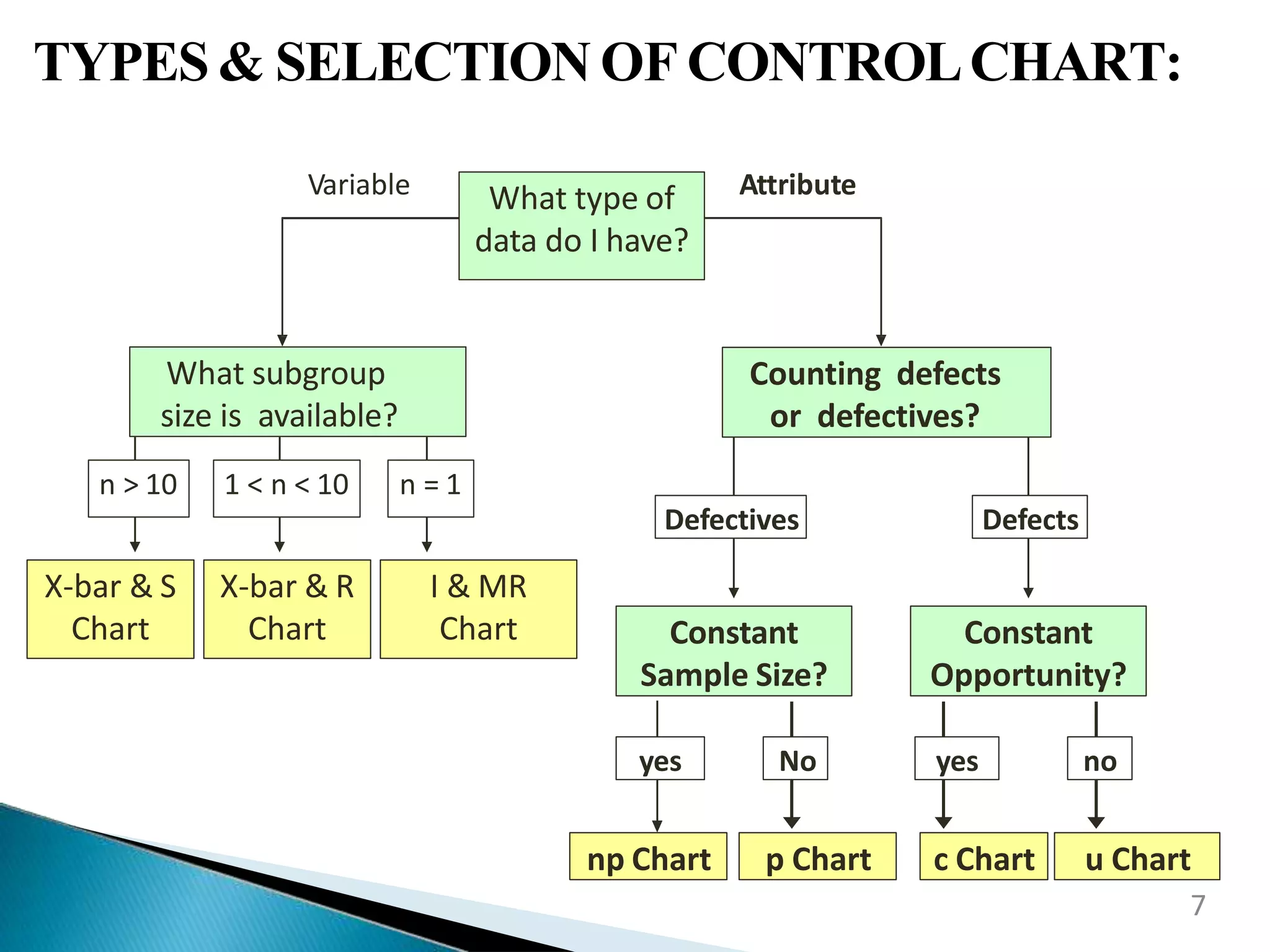
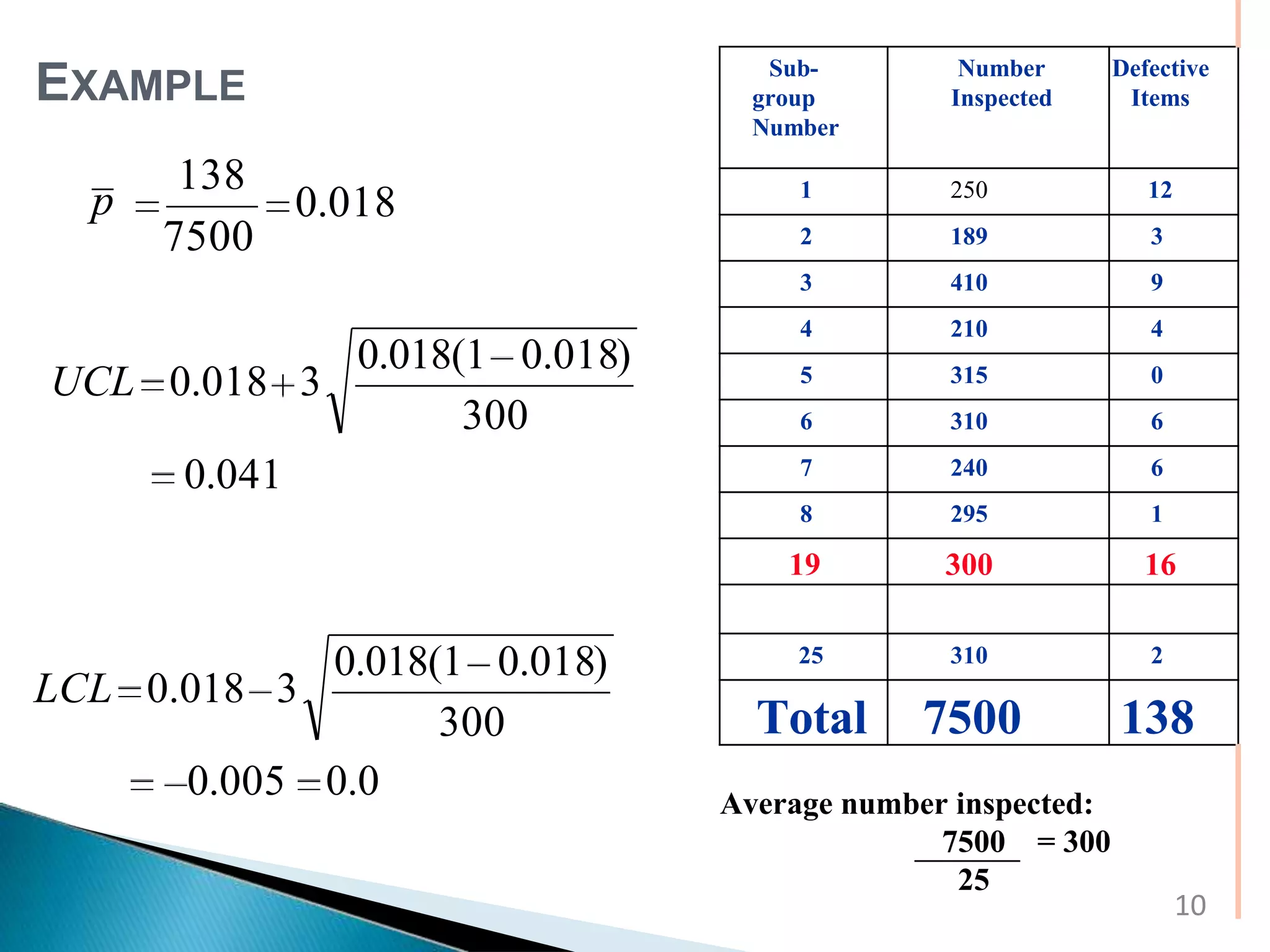
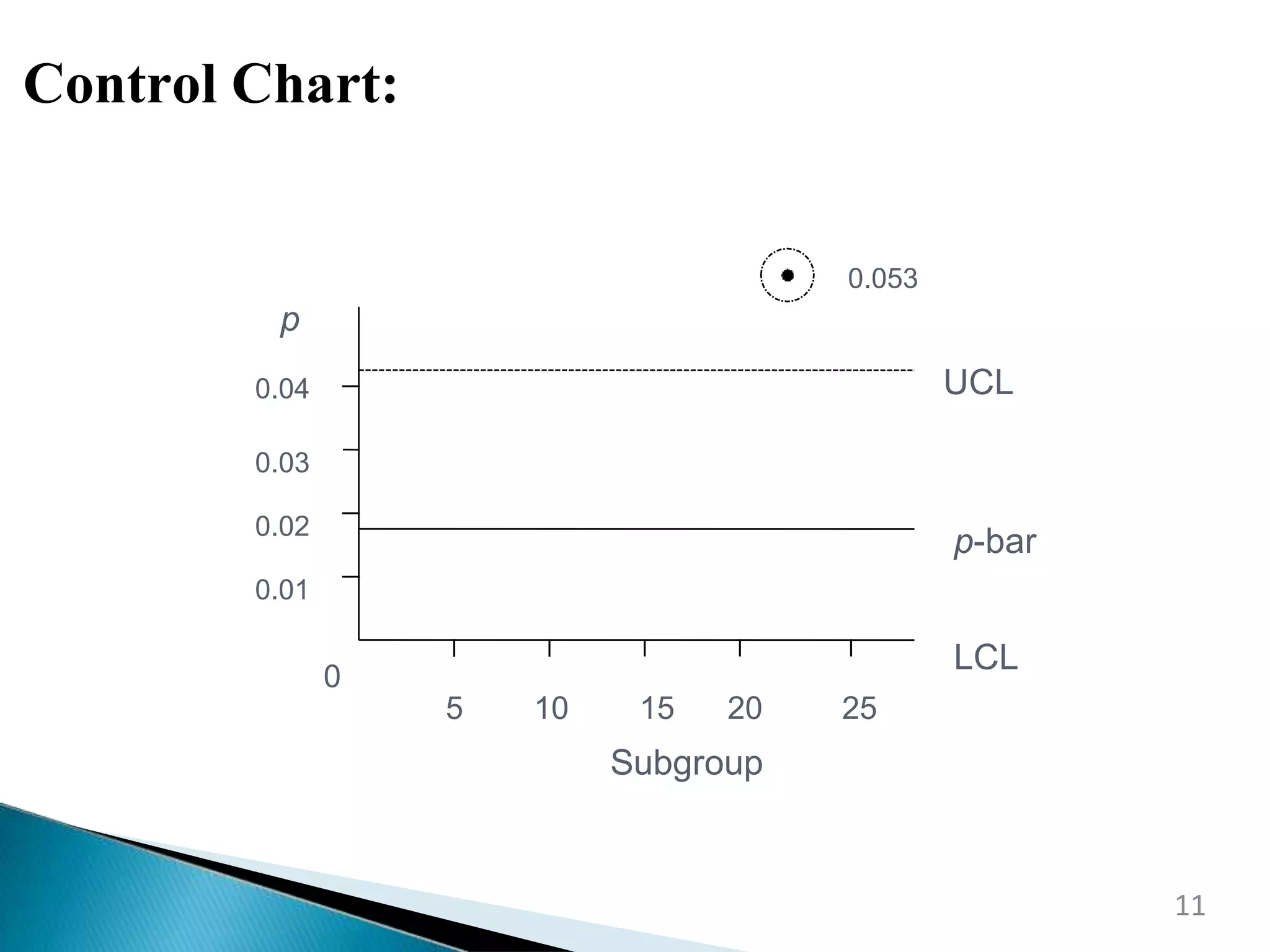
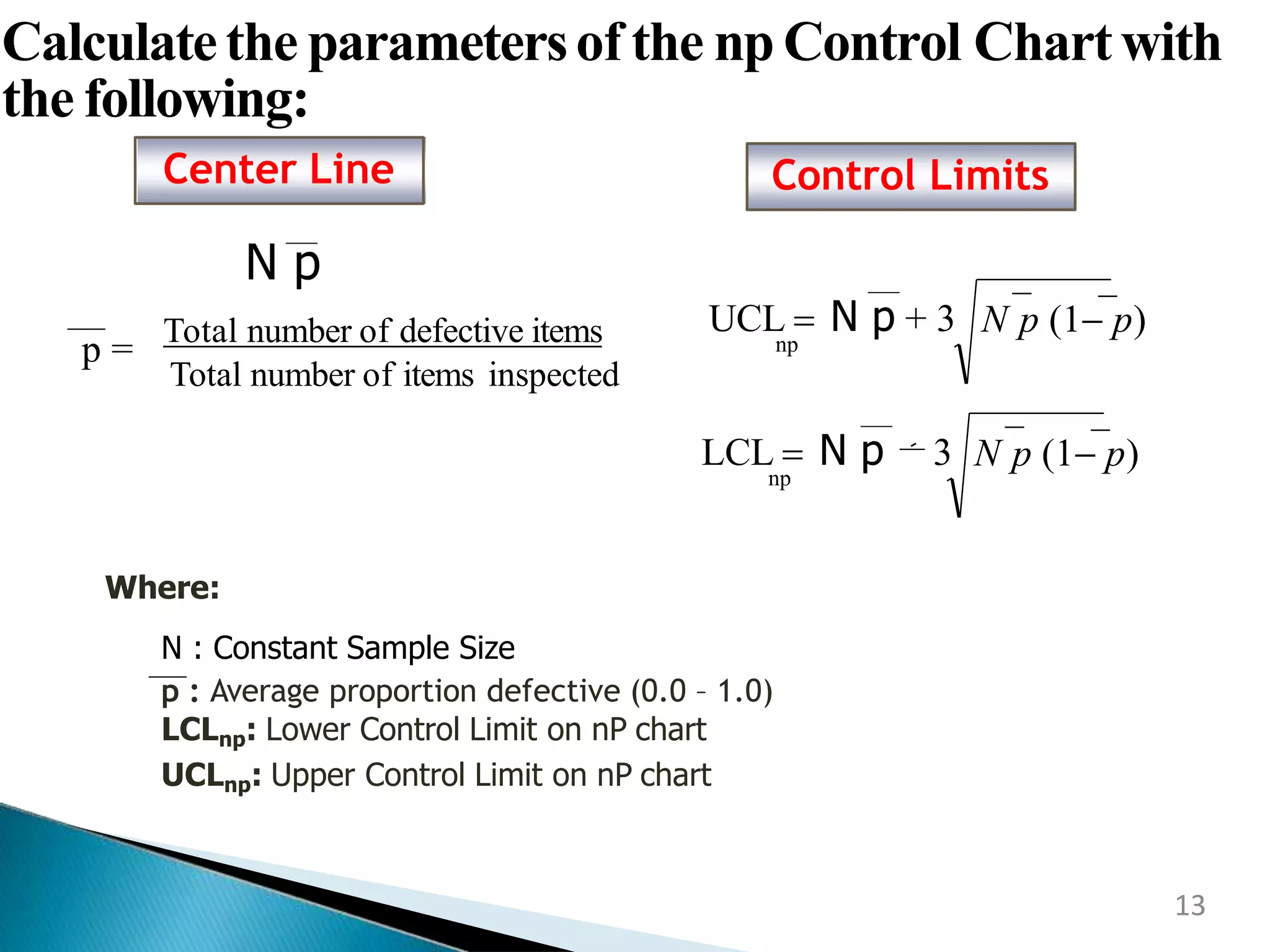
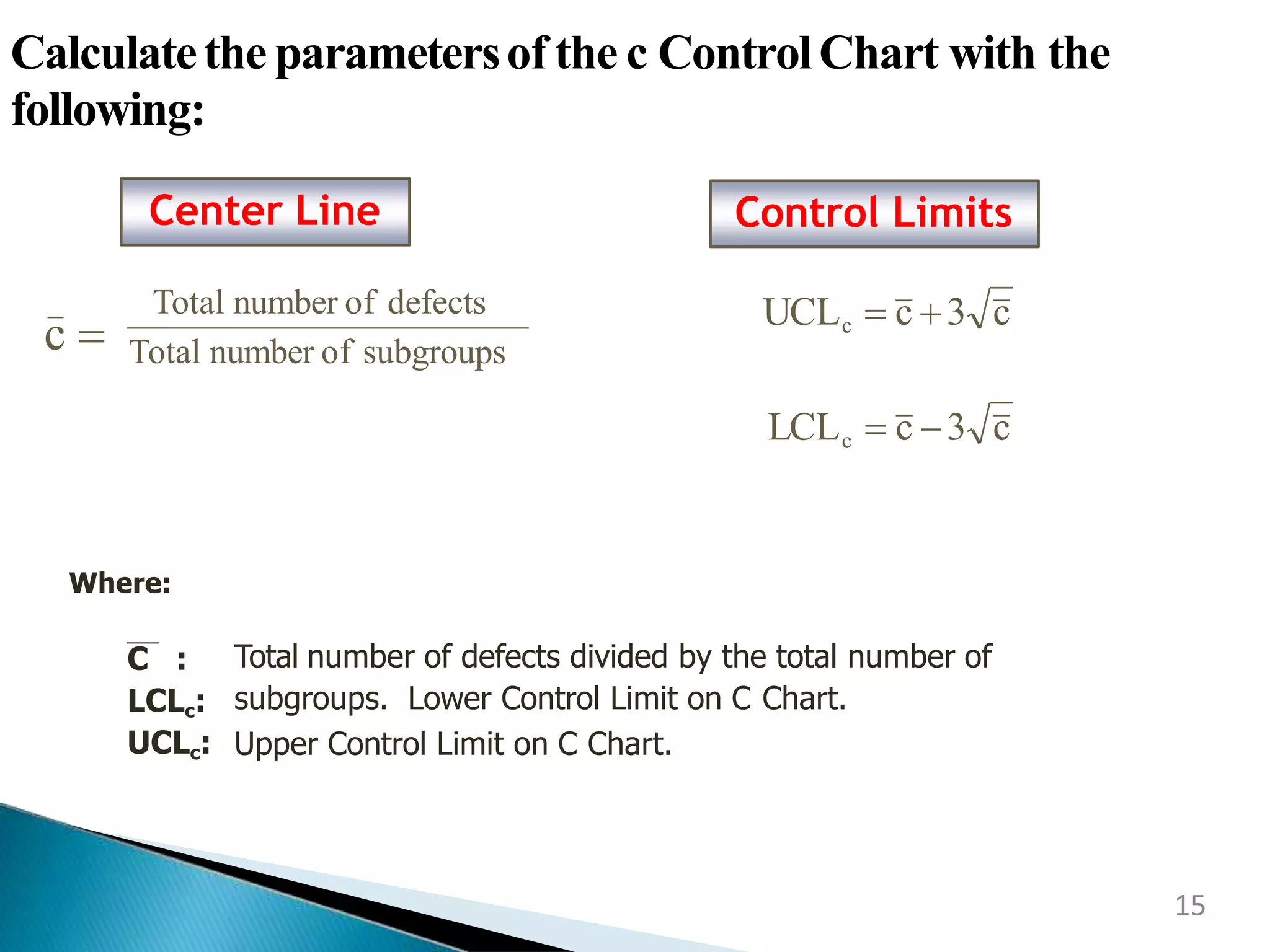
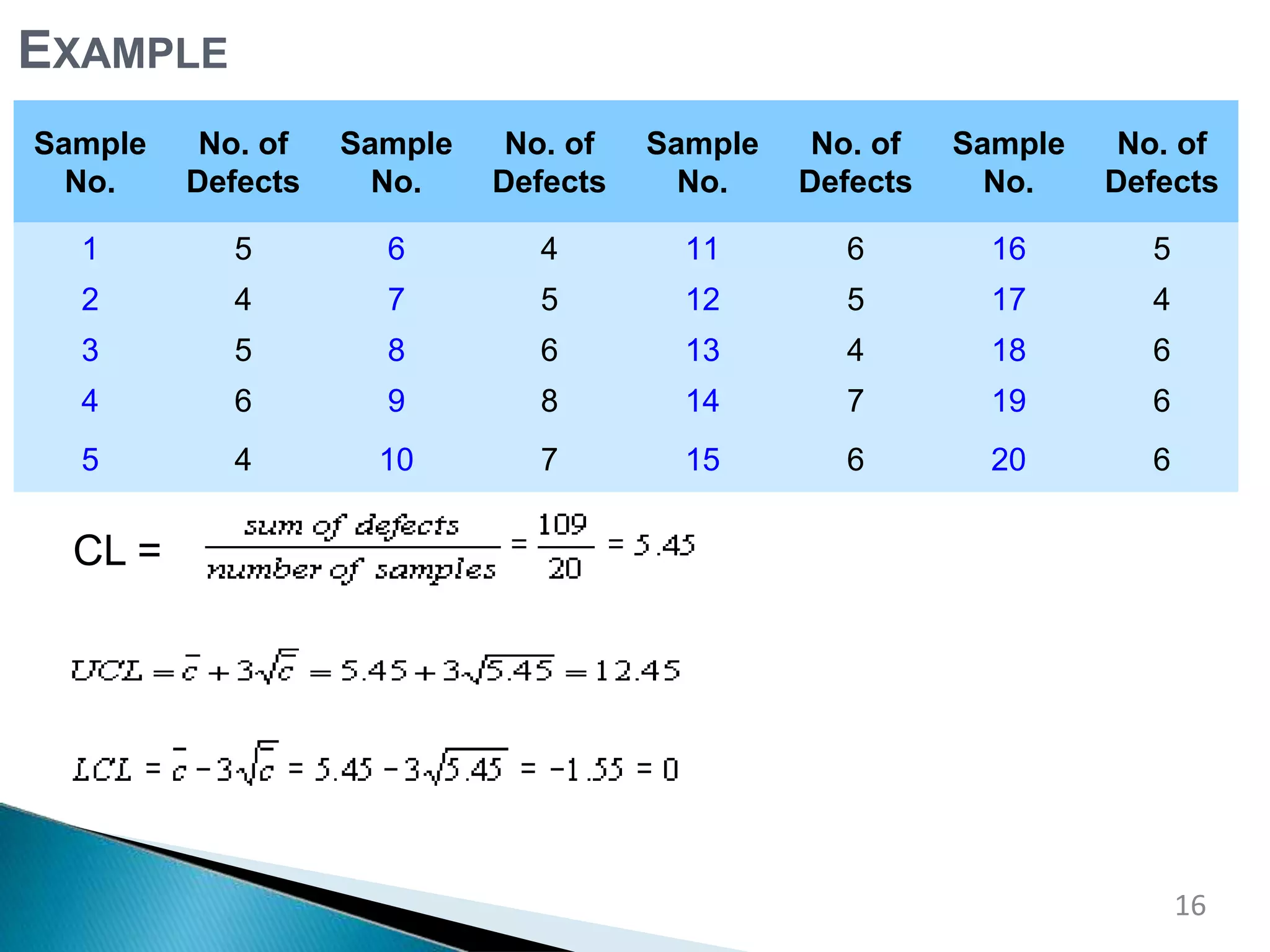
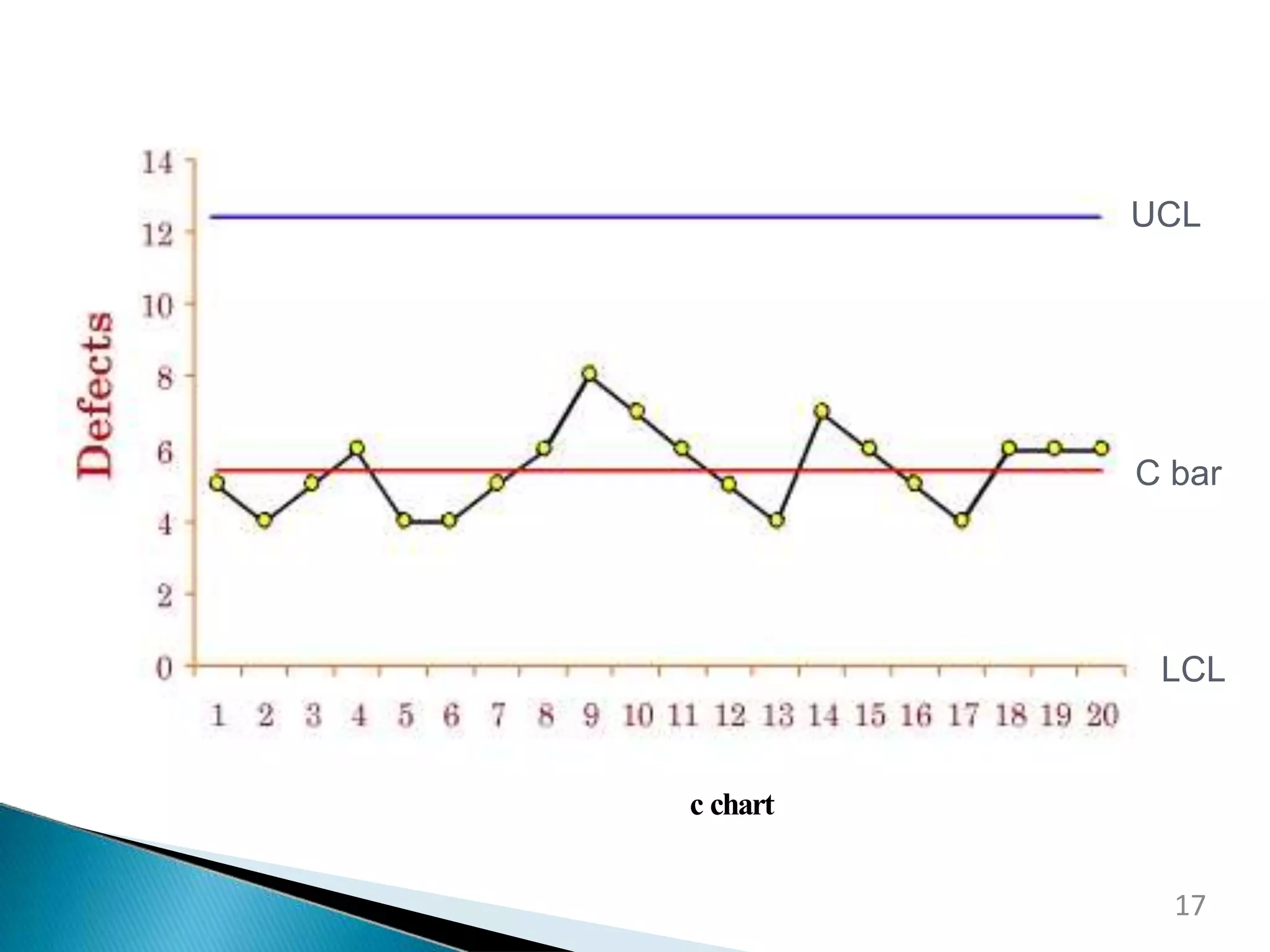
This document discusses control charts for attribute data. It defines an attribute as a quality characteristic that is either conforming or non-conforming. There are four main types of attribute control charts: p charts track the fraction of defective items, np charts track the number of defective items when sample sizes are constant, c charts track the number of defects when sample sizes are constant, and u charts track defects per unit when sample sizes vary. The document provides examples of how to calculate the parameters and create each type of attribute control chart. Advantages of attribute control charts include allowing for quick summaries by classifying items as acceptable or unacceptable and being easily understood by managers unfamiliar with quality control procedures.

1. 1

2. CONTROL CHARTS
(For Attributes)
Prepared by : VIPUL WADHWA
2

3. ◦ WHAT IS AN ATTRIBUTE?
◦ CONTROL CHARTS FOR ATTRIBUTE DATA
◦ TYPES & SELECTION OF CONTROL CHART
◦ WHAT IS p CHART , np CHART , c CHART , u CHART.
◦ CALCULATE THE PARAMETERS OF THE CONTROL
CHARTS
◦ ADVANTAGES OF ATTRIBUTE CONTROL CHARTS
Objectives :-
3

4. 4
The term Attribute refers to those quality characteristics
that conform to specifications or do not conform to
specifications. This data may be expressed as ok/not ok,
go/no go, yes/no, or presence/absence of a defect.
Attribute are used:
1. Where measurements are not possible.
2. Where measurements can be made but are not made
because of time, cost, or need.
◦What is an Attribute?

5. 5
CONTROLCHARTS FOR ATTRIBUTE DATA:
1. Nonconforming Units (based on the Binomial
distribution): p chart, np chart.
2. Nonconformities (based on the Poisson
distribution): c chart, u chart.

6. 6

7. 7
TYPES & SELECTION OF CONTROLCHART:
What type of
data do I have?
Variable Attribute
Counting defects
or defectives?
X-bar & S
Chart
I & MR
Chart
X-bar & R
Chart
n > 10 1 < n < 10 n = 1
Defectives Defects
What subgroup
size is available?
Constant
Sample Size?
Constant
Opportunity?
yes yesNo no
np Chart u Chartp Chart c Chart

8. 8
The p chart is for the fraction of defective items in a
sample/lot. This chart shows the fraction of nonconforming
or defective product produced by a manufacturing process.
The fraction defective is the number of defective items in a
sample divided by the total number of items in a sample.
The fraction defective chart is used when the sample size
varies.
What is p Chart:

9. 9
Calculatethe parametersof the p Control Chart
with thefollowing:
Where:
p: Average proportion defective (0.0 – 1.0)
ni: Average Number inspected in subgroups
LCLp: Lower Control Limit on p Chart
UCLp: Upper Control Limit on p Chart
Total number of defective items
Total number of items inspected
n
p
p(1 p)
UCL  p 3
Center Line Control Limits
in
p
i
p(1 p)
LCL  p 3
p =

10. 10
EXAMPLE
Sub-
group
Number
Number
Inspected
Defective
Items
1 250 12
2 189 3
3 410 9
4 210 4
5 315 0
6 310 6
7 240 6
8 295 1
19 300 16
25 310 2
Total 7500 138
Average number inspected:
7500 = 300
25
0.018
138
7500
p
300
0.018)0.018(1
LCL 0.018 3
0.005 0.0
0.041
300
0.018)0.018(1
UCL 0.018 3

11. 11
0.053
p-bar
LCL
UCL
p
5 10 15 20
Subgroup
25
0
0.01
0.02
0.03
0.04
Control Chart:

12. 12
What is np Chart:
When each data point is based on the same sample
size, a special version of the p chart can be used.
The np chart is for the number of defective items in
a sample.
This chart shows the number of nonconforming.
The number of defective, np, chart shows the number
of defective items in samples rather than the fraction
of defective items. It requires that the sample size
remains constant.

13. 13
Calculatethe parametersof the np Control Chartwith
the following:
Center Line Control Limits
Where:
N : Constant Sample Size
p : Average proportion defective (0.0 – 1.0)
LCLnp: Lower Control Limit on nP chart
UCLnp: Upper Control Limit on nP chart
N p
Total number of items inspected
p =
Total number of defective items UCL  N p + 3
np
N p (1 p)
LCL  N p 3
np
N p (1 p)

14. 14
What is c Chart:
The c chart is similar to the np chart, in that it requires
equal (constant) sample sizes for each data point.
This shows the number of defects or nonconformities
produced by a manufacturing process.
The number of defects (c chart) is based on the Poisson
distribution.

15. 15
Calculatethe parametersof the c ControlChart with the
following:
2
Center Line Control Limits
Total number of subgroups
Total number of defects
c 
UCLc  c 3 c
LCLc  c 3 c
Where:
C :
LCLc:
UCLc:
Total number of defects divided by the total number of
subgroups. Lower Control Limit on C Chart.
Upper Control Limit on C Chart.

16. 16
Sample
No.
No. of
Defects
Sample
No.
No. of
Defects
Sample
No.
No. of
Defects
Sample
No.
No. of
Defects
1 5 6 4 11 6 16 5
2 4 7 5 12 5 17 4
3 5 8 6 13 4 18 6
4 6 9 8 14 7 19 6
5 4 10 7 15 6 20 6
CL =
EXAMPLE

17. 17
c chart
LCL
UCL
C bar

18. 18
What is u Chart:
The u chart is a more general version of the c chart for use
when the data points do not come from equal-sized
samples.
The symbol u is used to represent defects per unit.
The u chart is used in cases where the samples are of
different size.
This chart shows the nonconformities per unit produced by a
manufacturing process.

19. 19
Calculate the parameters of the u Control Chart with the
following:
30
Center Line Control Limits
u 
Total number of defects Identified
Total number of Units Inspected
u
ni
UCLu  u 3
i
u
nuLCL  u 3
Where:
u: Total number of defects divided by the total number of units inspected.
ni : Average Number inspected in subgroup
LCLu: Lower Control Limit on U Chart.
UCLu: Upper Control Limit on U Chart.

20. 20
Advantages of attribute control charts:
Allowing for quick summaries, that is, the engineer
may simply classify products as acceptable or
unacceptable, based on various quality criteria.
Thus, attribute charts sometimes bypass the need for
expensive, precise devices and time-consuming
measurement procedures.
Easily understood by managers unfamiliar with
quality control procedures.

21. Thank you very much for your attention!
21