Downloaded 87 times
Uploaded bysanyogita .
Operating characteristic curves
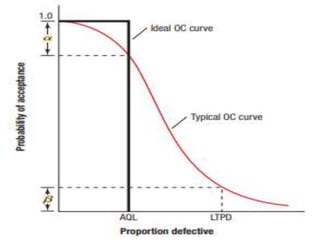
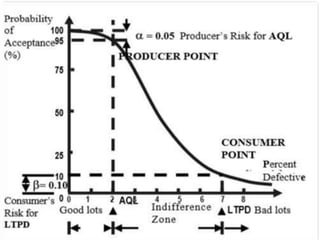
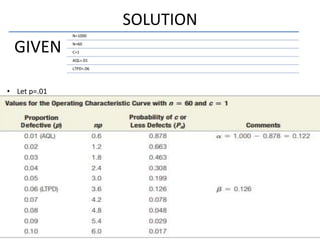
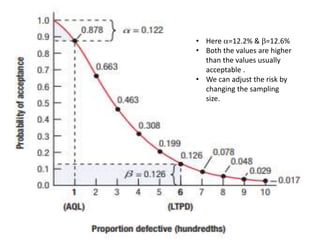
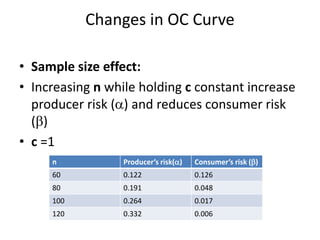
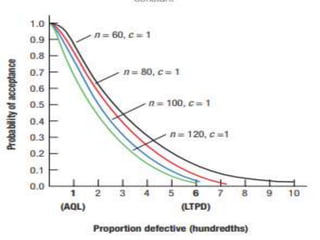
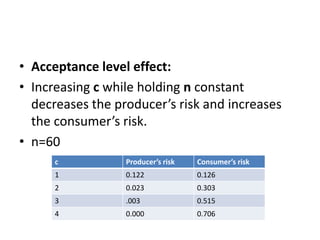
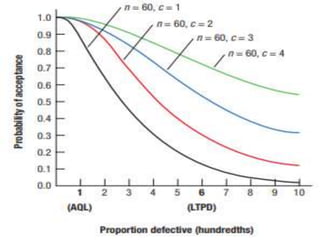
The document discusses operating characteristic (OC) curves, which are used in quality control to determine the probability of accepting production lots based on sampling inspections. An ideal OC curve would show 100% probability of acceptance for lots with defects below the acceptable quality level (AQL) and 0% above the AQL. Typical OC curves have an S-shape, plotting the probability of acceptance versus the fraction of defects. The curve shows the producer's risk of rejecting conforming lots and consumer's risk of accepting non-conforming lots. OC curves can be adjusted by changing the sample size or acceptance number to balance these risks.
More Related Content
![Oc Curves[1]](https://cdn.slidesharecdn.com/ss_thumbnails/occurves1-1226090108328626-9-thumbnail.jpg?width=640&height=640&fit=bounds)
Similar to Operating characteristic curves
Operating characteristic curves
- 1. Operating Characteristic Curves (AdvanceSampling Plan) SANYOGITA BE+MBA 4th YEAR CM14226
- 2. Operating Characteristic Curve •It is a graph used in quality control to determine the probability of accepting production lot. • The operating characteristic (OC) curve depicts the discriminatory power of an acceptance sampling plan. • The OC curve plots the probabilities of accepting a lot versus the fraction defective. • When the OC curve is plotted, the sampling risks are obvious.
- 3. Shape of OCCurve • Ideal OC curve • When percentage of Non-Conforming items are Below prescribed level Pa is 100%. And more than it makes Pa 0%. • Ideal OC Curve Can be Obtained By 100% Inspection. • Dividing line of Probability of acceptance Between 0 to 100% is AQL • No sampling plan give such a ideal OC Curve.
- 4. • Typical OCCurve: • This is Curve Roughly “S” Shaped. • Obtained by joining points between Probability of acceptance & Percentage non conforming items. • Obtained by Performing Sampling Inspection.
- 6. Specific Points inOC Curve • Producer’s Risks (α): • Probability of Rejection of a conforming lot. • To Reduce Producers Risk Produce Product at a better Quality Level Than AQL. • Value of Producer’s Risks is Commonly 5%. • =1-PA(at AQL)
- 7. • Consumer’s Risks(β): • Risk associated with Consumer. • Probability of accepting a non-conforming lot. • Usually it is 10%. • =PA(at LTPD)
- 8. • AQL(Acceptable QualityLevel): • Maximum Percent of defectives that will make lot easily acceptable. • Fraction of Defectives accepted without any serious effect on quality and customer relations. • PA for an AQL lot should be high. • AQL is also Termed as Producer’s “safe point”.
- 9. • Rejectable QualityLevel(RQL): • Quality Level Unacceptable to the Customer. • Definition Of Unsatisfactory Quality. • Characterised by low probability of acceptance. • PA of lot at RQL represents Consumer’s Risk.
- 11. DEFINATION OF VARIABLES •PA = The probability of acceptance • p = Proportion defective • N = Lot size • n = Sample size • c= Acceptance Number • α = Producer’s Risk • β= Consumer’s Risk
- 12. Steps for drawingOC Curve • Multiply proportion defective(p) with sample size (n) • Record the value for Probability of acceptance ,Pa from poisson probability distribution table • Then plot OC Curve i.e. proportion defective vs probability of acceptance. Given data Lot size N sample size n Acceptance size c AQL LTPD
- 13. EXAMPLE QUESTION • The NoiseKing Muffler Shop, a high-volume installer of replacement exhaust muffler systems, just received a shipment of 1,000 mufflers. The sampling plan for inspecting these mufflers calls for a sample size and an acceptance number . The contract with the muffler manufacturer calls for an AQL of 1 defective muffler per 100 and an LTPD of 6 defective mufflers per 100. Calculate the OC curve for this plan, and determine the producer’s risk and the consumer’s risk for the plan.
- 14.
- 15. • Here =12.2%& =12.6% • Both the values are higher than the values usually acceptable . • We can adjust the risk by changing the sampling size.
- 16. Changes in OCCurve • Sample size effect: • Increasing n while holding c constant increase producer risk () and reduces consumer risk () • c =1 n Producer’s risk() Consumer’s risk () 60 0.122 0.126 80 0.191 0.048 100 0.264 0.017 120 0.332 0.006
- 18. • Acceptance leveleffect: • Increasing c while holding n constant decreases the producer’s risk and increases the consumer’s risk. • n=60 c Producer’s risk Consumer’s risk 1 0.122 0.126 2 0.023 0.303 3 .003 0.515 4 0.000 0.706
- 20. • We shouldincrease the sample size, which reduces the consumer’s risk, and increase the acceptance number, which reduces the producer’s risk . • A improved combination can be found by trail and error.
- 21.
Editor's Notes
- #4 Pa is probability of acceptance