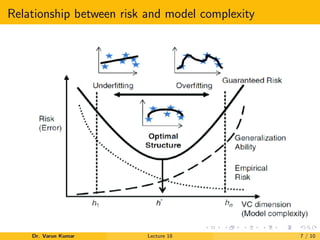
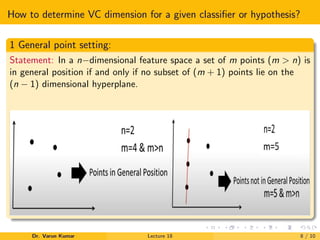
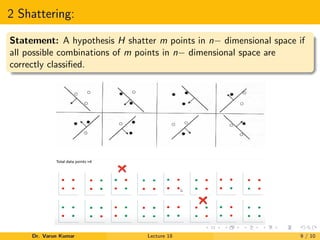
The document discusses VC dimension in machine learning. It introduces the concept of VC dimension as a measure of the capacity or complexity of a set of functions used in a statistical binary classification algorithm. VC dimension is defined as the largest number of points that can be shattered, or classified correctly, by the algorithm. The document notes that test error is related to both training error and model complexity, which can be measured by VC dimension. A low VC dimension or large training set size can help reduce the gap between training and test error.

1. VC Dimension in Machine Learning
Dr. Varun Kumar
Dr. Varun Kumar Lecture 18 1 / 10

2. Outlines
1 General Classification Problem
2 Usage of VC dimension in ML
3 Introduction to Vapnik-Chervonenkis (VC) Dimension
4 How to Determine VC Dimension for a Given Classifier or Hypothesis?
5 References
Dr. Varun Kumar Lecture 18 2 / 10

3. General classification problem
1 Always look for test error along with the training error.
2 Improving on training error does not improve the test error.
3 Increase in machine capacity may give the poor performance.
Is there any equation that relates the training and test error ?
Dr. Varun Kumar Lecture 18 3 / 10

4. Usage of VC dimension in ML
Model complexity determines the performance/cost on both the training
and test sets.
P
Test error ≤ Training error +
r
h(log(2N/h) + 1) − log η/4
N
= 1 − η
Note: Above expression shows the upper bound of test error with
probability 1 − η.
h→ VC dimension
h measure the power
h does not depend on the choice of training set
N → Total number of training sample
For reducing the residual, h → low or N → high
Test error ≤ Training error + Penalty(Complexity)
.
Dr. Varun Kumar Lecture 18 4 / 10

5. Continued–
⇒ Let us our training data are iid from some distribution fX (x).
⇒ Types of risk
(i) Risk R(θ)→ Long term observation→ Test observation
R(θ) = Test error = E[δ(c 6= ĉ(x; θ))]
(ii) Empirical risk Remp
(θ)→ Finite sample observation→ Training
observation
Remp
(θ) = Training error =
1
m
X
i
[δ(c(i)
6= ĉ(i)
(x; θ))]
Dr. Varun Kumar Lecture 18 5 / 10

6. Introduction to Vapnik-Chervonenkis (VC) Dimension
Key features:
⇒ VC dimension is a measure of the capacity (complexity, expressive
power, richness, or flexibility) of a set of functions.
⇒ It learns by a statistical binary classification algorithm.
⇒ It is defined as the cardinality of the largest set of points that the
algorithm can shatter.
Cardinality refers to the size of set. Ex- A = {1, 4, 6}, cardinality
|A| = 3
⇒ The capacity of a classification model is related to how complicated it
can be.→ Overfitting
VC dimension of a set-family
Let H be a set family (a set of sets) and C a set.
H ∩ C := {h ∩ C | h ∈ H}.
Dr. Varun Kumar Lecture 18 6 / 10

7. Relationship between risk and model complexity
Dr. Varun Kumar Lecture 18 7 / 10

8. How to determine VC dimension for a given classifier or hypothesis?
1 General point setting:
Statement: In a n−dimensional feature space a set of m points (m n) is
in general position if and only if no subset of (m + 1) points lie on the
(n − 1) dimensional hyperplane.
Dr. Varun Kumar Lecture 18 8 / 10

9. 2 Shattering:
Statement: A hypothesis H shatter m points in n− dimensional space if
all possible combinations of m points in n− dimensional space are
correctly classified.
Dr. Varun Kumar Lecture 18 9 / 10

10. References
E. Alpaydin, Introduction to machine learning. MIT press, 2020.
T. M. Mitchell, The discipline of machine learning. Carnegie Mellon University,
School of Computer Science, Machine Learning , 2006, vol. 9.
J. Grus, Data science from scratch: first principles with python. O’Reilly Media,
2019.
Dr. Varun Kumar Lecture 18 10 / 10