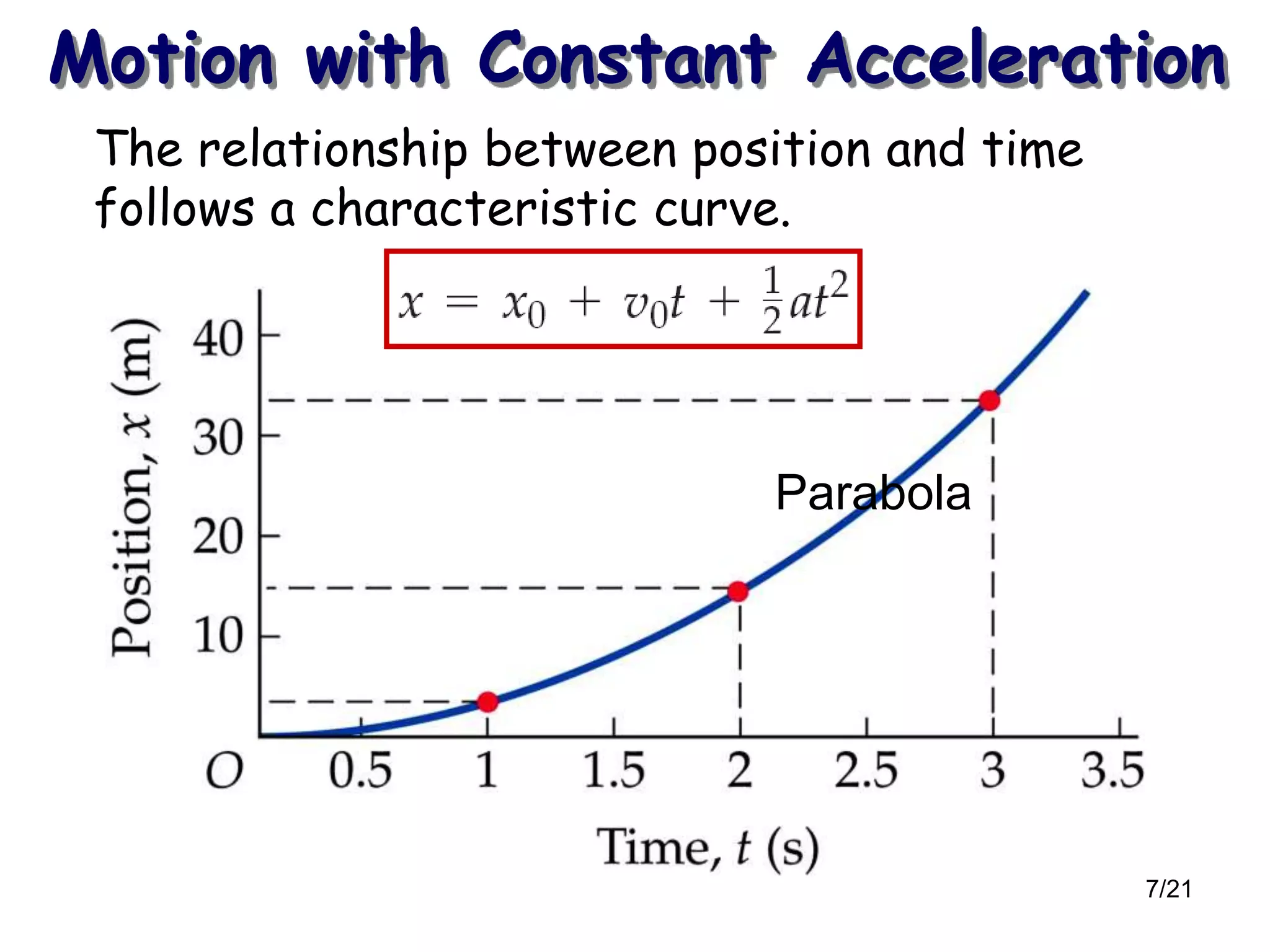
The document outlines a lecture schedule for a physics course focusing on mechanics, covering topics such as position, velocity, acceleration, equations of motion, and free fall. It includes details on weekly lectures, homework assignments, and laboratory sessions from January to February 2013. Key concepts include the equations of motion under constant acceleration and practical examples related to projectile motion and gravity.

1. Physics - Mechanics
Velocity and Acceleration
September , 2013
Dr. Muhammad Kamran
Department of Electrical Engineering
physics_ciit@hotmail.com

2. 2/21
Lecture Schedule (Part 1)
Physics - Introduction to Mechanics - -2013
Textbook: Physics, Vol. 1
Week Date L# Lecture Topic Pages Slides Reading HW Due Lab
1
7-Jan-13 1 Introduction to Physics 12 21 Chapter 1
No Lab 1st week
8-Jan-13 2 Position & Velocity 8 22 2-1 to 2-3
10-Jan-13 3 Velocity & Acceleration 10 25 2-4 to 2-5 No HW
11-Jan-13 4 Equations of Motion 9 21 2-6 to 2-7
2
14-Jan-13 5 Vectors 8 24 3-1 to 3-3
1-D Kinematics
15-Jan-13 6 r, v & a Vectors 5 24 3-4 to 3-5
17-Jan-13 7 Relative Motion 3 18 3-6 HW1
18-Jan-13 8 2D Motion Basics 5 19 4-1 to 4-2
3
21-Jan-13 H2 MLK Birthhday Holiday
Free Fall & Projectiles
22-Jan-13 9 2D Examples 13 22 4-3 to 4-5
24-Jan-13 R1 Review & Extension - 49 - HW2
25-Jan-13 E1 EXAM 1 - Chapters 1-4
We are here.

3. 3/21
Motion with Constant Acceleration

4. 4/21
Motion with Constant Acceleration
Velocity: (2-7)
Average velocity: (2-9)
Position as a function of time:
(2-10)
(2-11)
Velocity as a function of position:
(2-12)

5. 5/21
Motion with Constant
Acceleration, Other Variables (1)
0
0
v v v
v v at t
a a
 
    
0
0 av
av av
x x x
x x v t t
v v
 
    
v
a
t

 

6. 6/21
2
1 0 02
0 0 2
2v a x v
x x v t at t
a
   
    
Motion with Constant
Acceleration, Other Variables (2)
0
2
2( )x v t
a
t
 
 
2 2
0
2
v v
a
x

 

2 2
2 2 0
0 2
2
v v
v v a x x
a

     

7. 7/21
Motion with Constant Acceleration
The relationship between position and time
follows a characteristic curve.
Parabola

8. 8/21
Practice Clicker Question
Assume that the brakes on your car create a
constant deceleration, independent of how fast
you are going. Starting at a particular speed, you
apply the brakes and note the stopping distance D
and the stopping time T.
Now you double the speed of the car. How does
this change affect the stopping distance D and the
stopping time T?
(a) D and T remain the same.
(b) D and T both double (i.e., x2).
(c) D doubles and T quadruples (i.e., x4).
(d) D quadruples and T doubles.
(e) D and T both quadruple.

9. 9/21
Freely Falling Objects
An object falling in air is subject to air
resistance (and therefore is not freely falling).

10. 10/21
Freely Falling Objects
Free fall is the motion of an object subject
only to the influence of gravity. The
acceleration due to gravity is a constant, g.
We will
normally use
the value
g = 9.81 m/s2.
+

11. 11/21
Free Fall and g
One important example of constant
acceleration is the “free fall” of an
object under the influence of the
Earth’s gravity. The picture shows an
apple and a feather falling in vacuum
with identical motions.
The magnitude of this acceleration,
designated as g, has the approximate
value of a = g = 9.81 m/s2 = 32.2 ft/s2.
If downward is designated as the +y
direction, then a = +g; if downward is
designated as the y direction, then a =
g.
(Note that g is always positive., but
a may have either sign.)

12. 12/21
Freely Falling Objects
Free fall from rest
(with x = down):
0( )v t v gt 
1 2
0 0 2
( )x t x v t gt  

13. 13/21
Freely Falling Objects
Trajectory of a projectile:
Position
Velocity
Acceleration

14. 14/21
Upon graduation, a joyful student throws her cap straight
up in the air with an initial speed of 14.7 m/s. Given that its
acceleration has a magnitude of 9.81 m/s2 and is directed
downward (we neglect air resistance),
(a) When does the cap to reach its highest point?
(b) What is the distance to the highest point?
(c) Assuming the cap is caught at the same height it was
released, what is the total time that the cap is in flight?
Example: The Flying Cap
1. Draw the cap (as a dot) in its various positions.
2. (a) Use the time, velocity and acceleration relation.
(b) Use average velocity: vav = v0/2 = 7.35 m/s;
x = vav t = (7.35 m/s)(1.5 s) = 11.0 m
(c) Up time = down time, so total time is 3.0 s. (see text for a more
complicated method.)
3. The answers have the right units and seem reasonable.
0
0 2
(0 m/s) (14.7 m/s)
; 1.5 s
9.81 m/s
x x
x x x
x
v v
v v a t t
a
 
      


15. 15/21
Example: The Flying Cap
(continued)
The height of the cap vs. time has
the form of a parabola (since x ~ t2). It
is symmetric about the midpoint (but
would not be, if air resistance were
present).
The velocity of the cap vs. time has
the form of a straight line (since v ~ t).
The velocity crosses zero at the
midpoint and is negative thereafter,
because the cap is moving downward.

16. 16/21
An electron in a cathode-ray tube accelerates from rest with a constant
acceleration of 5.33 x 1012 m/s2 for 0.150 ms, then drifts with a constant
velocity for 0.200 ms, then slows to a stop with a negative acceleration of
2.67 x 1013 m/s2. (Note: 1 ms = 10-6 s)
How far does the electron travel?
Example: A Traveling Electron
1. Draw the electron (as a dot)
in its various positions xi.
2. Calculate the displacement xi and velocity vi for each part of the path:
1 12 -6 12 2 -6 2
1 0 2 2
(0 m/s)(0.150 10 s)+ (5.33 10 m/s )(0.150 10 s) 0.06 mxx v t a t       
3. The answers have the correct units and appear to be reasonable.
12 2 -6 5
1
5 -6
2 1 2
(5.33 10 m/s )(0.150 10 s) 8.0 10 m/s
(8.0 10 m/s)(0.200 10 s) 0.16 m
xv a t
x v t
     
     
2 2 2 5 2
2 2 0
0 3 13 2
(0 m/s) (8.0 10 m/s)
2 ; 0.012 m
2 2( 2.67 10 m/s )
x x
x x x
x
v v
v v a x x
a
  
      
 
1 1 1 (0.06 m) (0.16 m) (0.012 m) 0.232 m =23.2 cmx x x x         

17. 17/21
Example: Speed of a Lava Bomb
A volcano shoots out blobs of molten lava (lava
bombs) from its summit. A geologist observing the
eruption uses a stopwatch to time the flight of a
particular lava bomb that is projected straight upward.
If the time for it to rise and fall back to its launch
height is 4.75 s, what is its initial speed and how high
did it go? (Use g = 9.81 m/s2.)
1 12
0 0 02 2
0 ( )x x v t gt x t v gt       
1
0 2
Either 0 or 0t v gt  
1 1 2
0 2 2
(9.81 m/s )(4.75 s) 23.3 m/sv gt  
2 2
0At maximum height, 0 2v v g x   
2 2
0
2
(23.3 m/s)
27.7 m
2 2(9.81 m/s )
v
x
g
   