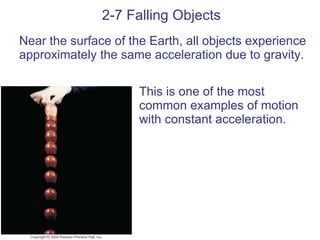
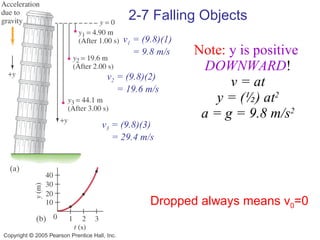
Chapter 2 introduces the concepts of kinematics including reference frames, displacement, velocity, acceleration, and motion with constant acceleration. Equations are derived that relate displacement, velocity, acceleration, and time for objects undergoing constant acceleration. Near the Earth's surface, the acceleration due to gravity is approximately 9.80 m/s2, so these equations can be applied to analyze falling or projected objects using this value of acceleration.

1. Chapter 2 Describing Motion: Kinematics in One Dimension

2. Units of Chapter 2 Reference Frames and Displacement Average Velocity Instantaneous Velocity Acceleration Motion at Constant Acceleration Solving Problems Falling Objects

3. Terminology Mechanics = Study of objects in motion. 2 parts to mechanics. Kinematics = Description of HOW objects move. Chapters 2 &3 No reference to WHY objects move. Dynamics = WHY objects move. Introduction of the concept of FORCE . Most of the course after Chapter 3.

4. Terminology Translational Motion = Motion with no rotation. Rectilinear Motion = Motion in a straight line path. (Chapter 2)

5. 2-1 Reference Frames and Displacement Any measurement of position, distance, or speed must be made with respect to a reference frame. For example, if you are sitting on a train and someone walks down the aisle, their speed with respect to the train is a few miles per hour, at most. Their speed with respect to the ground is much higher.

6. Define reference frame using a standard coordinate axes. 2 Dimensions (x,y) 3 Dimensions (x,y,z) (+,+) (-,+) (-,+) (-,-)

7. 2-1 Reference Frames and Displacement We make a distinction between distance and displacement . Displacement (blue line) is how far the object is from its starting point, regardless of how it got there. Distance traveled (dashed line) is measured along the actual path.

8. 2-1 Reference Frames and Displacement The displacement is written: ∆  Greek letter “ delta ” meaning “change in” Displacement is positive. Displacement is negative.

9. Vectors and Scalars Many quantities in physics, like displacement, have a magnitude and a direction . Such quantities are called VECTORS . Other quantities which are vectors: velocity, acceleration, force, momentum, ... Many quantities in physics, like distance, have a magnitude only . Such quantities are called SCALARS . Other quantities which are scalars: speed, temperature, mass, volume, ...

10. 2-2 Average Velocity Speed: how far an object travels in a given time interval (Scalar) Velocity includes directional information: (Vector) (2-1)

11. Walk for 70 s Average Speed = (100 m)/(70 s) = 1.4 m/s Average velocity = (40 m)/(70 s) = 0.57 m/s

12. 2-3 Instantaneous Velocity The instantaneous velocity is the average velocity, in the limit as the time interval becomes infinitesimally short. These graphs show (a) constant velocity and (b) varying velocity. (2-3) Evaluate in the limit of Δt approaching zero

13. 2-4 Acceleration Velocity can change with time. An object whose velocity is changing with time is said to be accelerating Acceleration is the rate of change of velocity.

14. The speed is increasing by 15 km/h every second

15. 2-4 Acceleration Acceleration is a vector, although in one-dimensional motion we only need the sign. The previous image shows positive acceleration; here is negative acceleration:

16. 2-4 Acceleration There is a difference between negative acceleration and deceleration: Negative acceleration is acceleration in the negative direction as defined by the coordinate system. Deceleration occurs when the acceleration is opposite in direction to the velocity.

17. 2-4 Acceleration The instantaneous acceleration is the average accelerati on , in the limit as the time interval becomes infinitesimally short. (2-5) Evaluate in the limit of Δt approaching zero

18. Let t 1 = t 0 = 0 and t 2 = t x 1 = x 0 ; x at t = 0 and x 2 = x ; x at t = t v 1 = v 0 ; v at t = 0 and v 2 = v ; v at t = t The average velocity of an object during a time interval t is The acceleration, assumed constant, is 2-5 Motion at Constant Acceleration (2-6) (2-2)

19. 2-5 Motion at Constant Acceleration In addition, as the velocity is increasing at a constant rate, we know that Combining these last three equations, we find: (2-8) (2-9)

20. 2-5 Motion at Constant Acceleration We can also combine these equations so as to eliminate t : We now have all the equations we need to solve constant-acceleration problems. (2-10) (2-11a) (2-11b) (2-11c) (2-11d) Not valid unless a is constant

21. 2-6 Solving Problems Read the whole problem and make sure you understand it. Then read it again. Decide on the objects under study and what the time interval is. Draw a diagram and choose coordinate axes. Write down the known (given) quantities, and then the unknown ones that you need to find. What physics applies here? Plan an approach to a solution.

22. 2-6 Solving Problems 6. Which equations relate the known and unknown quantities? Are they valid in this situation? Solve algebraically for the unknown quantities, and check that your result is sensible (correct dimensions). 7. Calculate the solution and round it to the appropriate number of significant figures. 8. Look at the result – is it reasonable? Does it agree with a rough estimate? 9. Check the units again.

23. Example 2-6 Known wanted x 0 = v 0 = x = a = v 0 0 150 m 2.00 m/s 2 a) b)

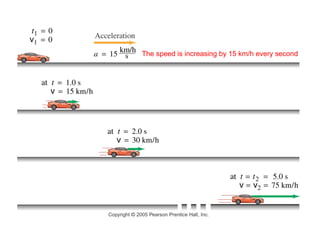
24. Example 2-9, Estimate Breaking Distances v = v 0 = constant = 14 m/s t = 0.50 s a = 0 x = v 0 t = 7 m a = - 6.0 m/s 2 v decreases from 14 m/s to zero x 0 = 7 m, v 0 = 14 m/s, v = 0 v 2 = (v 0 ) 2 + 2a(x – x 0 )  x = x 0 + [v 2 - (v 0 ) 2 ]/(2a) = 7 m + 16 m = 23 m  

25. 2-7 Falling Objects Near the surface of the Earth, all objects experience approximately the same acceleration due to gravity. This is one of the most common examples of motion with constant acceleration.

26. 2-7 Falling Objects In the absence of air resistance, all objects fall with the same acceleration, although this may be hard to tell by testing in an environment where there is air resistance. clip

27. To treat motion of falling objects, use the same equations we already have (one dimensional uniform acceleration equations) with the following changes: 1) The acceleration due to gravity at the Earth’s surface is approximately 9.80 m/s 2 . Replace a by g = 9.8 m/s 2 2) Usually, we consider vertical motion to be in the y direction, so replace x by y and x 0 by y 0 (usually y 0 = 0 )

28. Sign of g in 1-d Equations Magnitude ( size ) of g = 9.8 m/s 2 ( POSITIVE !) But, acceleration is a vector (1- dim), with 2 possible directions. Call these + and - . May seem “natural” for “up” to be + y and “down” to be - y , but we could also choose (we sometimes will!) “down” to be + y and “up” to be - y In equations g could have a + or a - sign in front of it, depending on our choice!

29. Directions of Velocity & Acceleration Objects in free fall ALWAYS have downward acceleration. Still use the same equations for objects thrown upward with some initial velocity v 0 An object goes up until it stops at some point & then it falls back down. Acceleration is always g in the downward direction. For the first half of flight, the velocity is UPWARD .  For the first part of the flight, velocity & acceleration are in opposite directions !

30.  VELOCITY & ACCELERATION ARE NOT NECESSARILY IN THE SAME DIRECTION!

31. Equations for Bodies in Free Fall Written taking “up” as + y ! v = v 0 - g t (1) y = y 0 + v 0 t – ( ½) gt 2 (2) v 2 = (v 0 ) 2 - 2g (y - y 0 ) (3) v = ( ½) (v + v 0 ) (4) g = 9.8 m/s 2 Usually y 0 = 0 . Sometimes v 0 = 0

32. Equations for Bodies in Free Fall Written taking “down” as + y ! v = v 0 + g t (1) y = y 0 + v 0 t + ( ½) gt 2 (2) v 2 = (v 0 ) 2 + 2g (y - y 0 ) (3) v = ( ½) (v + v 0 ) (4) g = 9.8 m/s 2 Usually y 0 = 0 . Sometimes v 0 = 0

33. 2-7 Falling Objects Note: y is positive DOWNWARD ! v = at y = (½) at 2 a = g = 9.8 m/s 2 v 1 = (9.8)(1) = 9.8 m/s v 2 = (9.8)(2) = 19.6 m/s v 3 = (9.8)(3) = 29.4 m/s Dropped always means v 0 =0

34. Examples 2-12 & 2-14 Before the ball is released upward, it’s under both g and a . As soon as it leaves the man’s hand, it’s only under g

35. Summary of Chapter 2 Kinematics is the description of how objects move with respect to a defined reference frame. Displacement is the change in position of an object. Average speed is the distance traveled divided by the time it took; average velocity is the displacement divided by the time. Instantaneous velocity is the limit as the time becomes infinitesimally short.

36. Summary of Chapter 2 Average acceleration is the change in velocity divided by the time. Instantaneous acceleration is the limit as the time interval becomes infinitesimally small. The equations of motion for constant acceleration are given in the text; there are four, each one of which requires a different set of quantities. Objects falling (or having been projected) near the surface of the Earth experience a gravitational acceleration of 9.80 m/s 2 .