Maxwell derived a set of equations that unified electricity, magnetism and light as manifestations of electromagnetic waves. His equations predicted that changes in electric and magnetic fields propagate as waves at the speed of light. This supported Maxwell's theory that light itself is an electromagnetic wave. The electromagnetic spectrum encompasses all possible frequencies of electromagnetic waves, from radio waves to gamma rays. Maxwell's equations form the basis for the modern understanding of electromagnetism and optics.

1. ELECTROMAGNETIC WAVES
• Types of electromagnetic waves
• Electromagnetic spectrum
• Propagation of electromagnetic wave
• Electric field and magnetic field
• Qualitative treatment of electromagnetic waves

2. • Electromagnetic (EM) waves were first postulated by James Clerk
Maxwell and subsequently confirmed by Heinrich Hertz
• Maxwell derived a wave form of the electric and magnetic equations,
revealing the wave-like nature of electric and magnetic fields, and
their symmetry
• Because the speed of EM waves predicted by the wave equation
coincided with the measured speed of light, Maxwell concluded
that light itself is an EM wave
• According to Maxwell’s equations, a spatially-varying electric
field generates a time-varying magnetic field and vice versa
• Therefore, as an oscillating electric field generates an oscillating
magnetic field, the magnetic field in turn generates an oscillating
electric field, and so on
• These oscillating fields together form an electromagnetic wave
Introduction

3. • In the studies of electricity and magnetism, experimental
physicists had determined two physical constants - the electric
(o) and magnetic (o) constant in vacuum
• These two constants appeared in the EM wave equations, and
Maxwell was able to calculate the velocity of the wave (i.e. the
speed of light) in terms of the two constants:
• Therefore the three experimental constants, o, o and c
previously thought to be independent are now related in a fixed
and determined way
Speed of EM waves
m/s100.3
1 8
oo


c 0 = 8.8542  10-12 C2 s2/kgm3 (permittivity of vacuum)
0 = 4  10-7 kgm/A2s2 (permeability of vacuum)

4. Name Differential form Integral form
Gauss's law
Gauss's law for
magnetism
Maxwell–Faraday
equation (Faraday's law of
induction)
Ampère's circuital law
(with Maxwell's correction)
Formulation in terms of free charge and current
Maxwell’s Equations
fD 

t
B
E





0 B

0
AdB
V

)(VQAdD f
V


t
ldE SB
S 


,

t
D
JH





t
IldH SD
fS
S 


,
,

z
z
y
y
x
x
ˆˆˆ








 v
z
v
y
v
x
v
vdiv zyx 










zyx
zyx
vvv
zyx
v 






ˆˆˆ


5. Maxwell’s Equations
Formulation in terms of total charge and current
0

 E

t
B
E





0 B

t
E
JB





000
0
)(


VQ
AdE
V

t
ldE SB
S 


,

0
AdB
V

t
IldB SE
S
S 


,
000

Differential form Integral form
Gauss's law
Gauss's law for
magnetism
Maxwell–Faraday equation
(Faraday's law of induction)
Ampère's circuital law
(with Maxwell's correction)

6. line integral of the electric field along the
boundary ∂S of a surface S (∂S is always a
closed curve)
line integral of the magnetic field over the
closed boundary ∂S of the surface S
The electric flux (surface integral of the
electric field) through the (closed)
surface (the boundary of the volume V )
The magnetic flux (surface integral of the
magnetic B-field) through the (closed)
surface (the boundary of the volume V )
Maxwell’s Equations
ldE
S


ldB
S


AdE
V


AdB
V



7. (1) Gauss’s law for the electric field
Gauss’s law is a consequence of the inverse-square nature of Coulomb’s
law for the electrical force interaction between point like charges
(2) Gauss’s law for the magnetic field
This statement about the non existence of magnetic monopole; magnets are
dipolar. Magnetic field lines form closed contours
(4) The Ampere-Maxwell law
This law is a statement that magnetic fields are caused by electric conduction
currents and or by a changing electric flux (via the displacement current)
(3) Faraday’s law of electromagnetic induction
This is a statement about how charges in magnetic flux produce
(non-conservative) electric fields
Maxwell’s Equations

8. Electromagnetic Spectrum

9. Generating an Electromagnetic Waves
An arrangement for generating a traveling electromagnetic
wave in the shortwave radio region of the spectrum: an LC
oscillator produces a sinusoidal current in the antenna, which
generate the wave. P is a distant point at which a detector can
monitor the wave traveling past it

10. Generating an Electromagnetic Waves
Variation in the electric field E and the
magnetic field B at the distant point P as
one wavelength of the electromagnetic
wave travels past it.
The wave is traveling directly out of the
page
The two fields vary sinusoidally in
magnitude and direction
The electric and magnetic fields are always
perpendicular to each other and to the
direction of travel of the wave

11. • Close switch and current flows briefly. Sets up electric field
• Current flow sets up magnetic field as little circles around the wires
• Fields not instantaneous, but form in time
• Energy is stored in fields and cannot move infinitely fast
Generating an Electromagnetic Waves

12. • Figure (a) shows first half cycle
• When current reverses in Figure (b), the fields reverse
• See the first disturbance moving outward
• These are the electromagnetic waves
Generating an Electromagnetic Waves

13. • Notice that the electric and
magnetic fields are at right
angles to one another
• They are also perpendicular
to the direction of motion of
the wave
Generating an Electromagnetic Waves

14. Electromagnetic Waves
• The cross product always gives the direction of travel
of the wave
• Assume that the EM wave is traveling toward P in the positive
direction of an x-axis, that the electric field is oscillating parallel
to the y-axis, and that the magnetic filed is the oscillating
parallel to the z-axis:
)sin(
)sin(
0
0
tkxBB
tkxEE


E0 = amplitude of the electric field
B0 = amplitude of the magnetic field
 = angular frequency of the wave
k = angular wave number of the wave
At any specified time and place: E/B = c
cBE 00
/
(speed of electromagnetic wave)
BE



15. Electromagnetic wave represents the transmission of energy
The energy density associated with the electric field in free space:
2
0
2
1
EuE 
The energy density associated with the magnetic field in free space:
2
0
1
2
1
BuB


Electromagnetic Waves
BEBE uuuuu 22 Total energy density:
2
0
2
0
1
BEu



16. Example
Imagine an electromagnetic plane wave in vacuum whose electric field (in
SI units) is given by
0,0),109103(sin10 1462
 zyx EEtzE
Determine (i) the speed, frequency, wavelength, period, initial phase and
electric field amplitude and polarization, (ii) the magnetic field.
Solution
(i) The wave function has the form: )(sin),( 0 vtzkEtzE xx 
)]103(103sin[10Here, 862
tzEx 
1816
ms103,m103 
 vk
Hz105.4,nm7.666
2 14





v
f
k

17. Solution (continued)
Period , and the initial phase = 0s102.2/1 15
 fT
Electric field amplitude V/m102
0 xE
The wave is linearly polarized in the x-direction and
propagates along the z-axis
(ii) The wave is propagating in the z-direction whereas the electric
field oscillates along the x-axis, i.e. resides in the xz-plane.
Now, is normal to both and z-axis, so it resides in the yz-
plane. Thus,
E

B

E

),(ˆand,0,0 tzBjBBB yzx 

Since, cBE 
T)109103(sin1033.0),( 1466
tztzBy  

18. refer to the fields of a wave at a particular point in space and
indicates the Poynting vector at that point
Energy Transport and the Poynting VectorS

• Like any form of wave, an EM wave can transport from one location to
another, e.g. light from a bulb and radiant heat from a fire
• The energy flow in an EM is measured in terms of the rate of energy flow
per unit area
• The magnitude and direction of the energy flow is described
in terms of a vector called the Poynting vector: S

BES




0
1
B,E

S

is perpendicular to the plane formed
by , the direction is determined
by the right-hand rule.
S

BE

and

19. Energy Transport and the Poynting VectorS

Because are perpendicular to each other in an EM wave, the
magnitude of is:
BE

and
S

EBS
0
1

 2
E
c
S
0
1

E/cB  Instantaneous
energy flow rate
Intensity I of the wave = time average of S, taken over one or more
cycles of the wave
)(sin
11 22
00
tkxE
c
E
c
SI m
2





rmsrmsrms BEE
c
SI
0
2
0
1
2
1




In terms of rms :
rmsm EE 2
mmm BEE
c
I
0
2
0 2
1
2
1





20. Example
[source: Halliday, Resnick, Walker, Fundamentals of Physics 6th Edition, Sample Problem 34-1
An observer is 1.8 m from a light source whose power Ps is 250 W. Calculate the rms
values of the electric and magnetic fields due to the source at the position of the
observer.
Energy Transport and the Poynting VectorS

0
2
2
4 



c
E
r
P
I rms
V/m48
)m8.1(4
H/m)10m/s)(4π10(250W)(3
4 2
78
2
0








r
Pc
Erms
T106.1
m/s103
V/m48 7
8




c
E
B rms
rms

21. Polarization of
Electromagnetic Wave

22. Polarization of Electromagnetic Wave
The transverse EM wave is said to be polarized (more
specifically, plane polarized) if the electric field vectors are
parallel to a particular direction for all points in the wave
direction of the electric field vector E = direction of polarization
xtkzEE ˆ)sin(0 

Example, consider an electric field propagating in the positive
z-direction and polarized in the x-direction
ytkzE
c
B ˆ)sin(
1
0 







ztkzEcS ˆ)sin(2
00 
BES




0
1
oo
1

c

23. Example
A plane electromagnetic harmonic wave of frequency 6001012 Hz,
propagating in the positive x-direction in vacuum, has an electric field
amplitude of 42.42 V/m. The wave is linearly polarized such that the
plane of vibration of the electric field is at 45o to the xz-plane. Obtain
the vector BE

and
Solution
:bygivenisvectorelectricThe E

here   2/12
0
2
00,0 zyx EEEE 













 8
12
0
103
106002sin
x
tEE

1
02
1
00 Vm30 
 EEE zy
x
y
z

24. Solution (continued)
So













 8
12
103
106002sin30,0
x
tEEE zyx













 
8
127
103
106002sin10,0
x
tBBB yzx
cBE 
)ˆˆ(ˆˆ kjEkEjEE yzy 

)ˆˆ(ˆˆ kjBkBjBB yzy 

BEBE

tonormalis,0Then 
required.as,ˆ
2
)ˆˆ(and
2
i
c
E
iiBEBES
y
zy 


25. Harmonic Waves
)](sin[ txkAy v
)sin( tkxAy 
A = amplitude k = 2/ (propagation constant)
)](cos[ txkAy vor
v = f  = f (2/k) k v = 2f =  (angular frequency)
)cos( tkxAy or
Phase :  = k(x + vt) = kx + t  moving in the – x-direction
 = k(x - vt) = kx - t  moving in the + x-direction

26. Harmonic Waves
)sin( 0 tkxAy
In general, to accommodate any arbitrary initial displacement,
some angle 0 must be added to the phase, e.g.
Suppose the initial boundary conditions are such that y = y0
when x = 0 and t = 0 , then
y = A sin 0 = y0
 0 = sin-1 (y0/A)

27. Plane Waves
The wave “displacement” or disturbance y at spatial
coordinates (x, y, z): )sin( tkxAy 
 Traveling wave moving along the +x-direction
At fixed time, let take at t = 0: kxAy sin
When x = constant, the phase  = kx = constant
 the surface of constant phase are a family of planes
perpendicular to the x-axis
 these surfaces of constant phase are called the wavefronts

28. Plane Waves
Plane wave along x-axis. The waves penetrate the
planes x = a, x = b, and , x = c at the points shown

29. Plane Waves
Generalization of the plane wave to an
arbitrary direction. The wave direction is
given by the vector k along the x-axis in (a)
and an arbitrary direction in (b)
x= r cos
)cossin(  krAy
)sin( tAy  rk

zyx xkxkxk rk

)( zyx k,k,k
are the components
of the propagation
direction
)( ti
Aey 
 rk


30. Spherical & Cylindrical Waves
Spherical Waves:
Cylindrical Waves:
)( tkri
e
r
A
y 

)( tki
e
A
y 



r = radial distance from the point source to a given point
on the waveform
A/ r = amplitude
 = perpendicular distance from the line of symmetry to a
point on the waveform
e.g. of the z-axis is the line of symmetry, then 22
yx 

31. Mathematical Representation of Polarized Light
yExEE yx ˆˆ 

Consider an EM wave propagating along the
z-direction of the coordinate system shown in
figure.
The electric field of this wave at the origin of
the axis system is given by:
z
x
y
E

xE
yE
0
Propagation
direction
Complex field components for waves traveling in the +z-direction
with amplitude E0x and E0y and phases x and y :
)(
0
~ xtkzi
xx eEE 
 )(
0
~ xtkzi
yy eEE 

 xx EE
~
Re  yy EE
~
Re

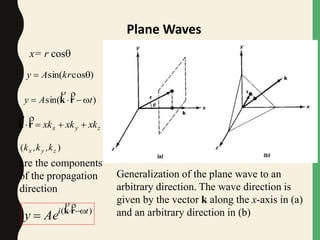
32. yxE ˆˆ
~ )(
0
)(
0
yx
tkzi
y
tkzi
x eEeE


)(
0
)(
00
~~
ˆˆ[
~
tkzi
tkzii
y
i
x
e
eeEeE yx




EE
]yxE
]ˆˆ[
~
000 yxE yx
i
y
i
x eEeE

 = complex amplitude vector for the polarized wave
Since the state of polarization of the light is completely determined
by the relative amplitudes and phases of these components, we
just concentrate only on the complex amplitude, written as a two-
element matrix – called Jones vector:

















 

y
x
i
y
i
x
y
x
eE
eE
E
E
0
0
0
0
0 ~
~
~
E
Mathematical Representation of Polarized Light

33. Linear Polarization
Figures representation of -vectors of linearly polarized light with
various special orientations. The direction of the light is along the z-axis
oscillations along
the y-axis between
+A and A
Vertically polarized Horizontally polarized Linearly polarized
+A
A
linear
polarization
along y






















1
00~
0
0
0 A
AeE
eE
y
x
i
y
i
x


E
E

E


34. Linear Polarization






1
0
= Jones vector for vertically linearly polarized light






b
a
= vector expression in normalized from for 1
22
 ba
In general:

35. Linear Polarization
AEE xxy  00 ,0,0





















 

0
1
0
~
0
0
0 A
A
eE
eE
y
x
i
y
i
x
E
linear
polarization
along x
Horizontally polarized
+A-A

36. Linear Polarization
0
cos,sin 00


yx
yx AEAE

























 

sin
cos
sin
cos~
0
0
0 A
A
A
eE
eE
y
x
i
y
i
x
E
linear
polarization
at 
oscillations along the a
line making angle  with
respect to the x-axis
E

Linearly polarized

37. 


















3
1
2
1
2/3
2/1
60sin
60cos~
0E
Linear Polarization
For example  = 60o :







b
a
0
~
EGiven a vector a, b = real numbers
the inclination of the corresponding linearly polarized light is given by














 
ox
oy
E
E
a
b 11
tantan

38. Suppose  = negative angle
 E0y = negative number
Since the sine is an odd function, thus
E0x remain positive
The negative sign ensures that the two vibrations are  out of phase, as
needed to produce linearly polarized light with -vectors lying in the
second and fourth quadrants
E

The resultant vibration takes places place along a line with negative slope






b
a
Jones vector with both a and b real numbers, not both zero,
represents linearly polarized light at inclination angle 





 
a
b1
tan
Linear Polarization

39. • In determining the resultant vibration due to two
perpendicular components, we are in fact determining
the appropriate Lissajous figure
• If  other than 0 or , the resultant E-vector traces out
an ellipse
Lissajous Figures

40. Lissajous figures as a function of relative phase for orthogonal vibrations of
unequal amplitude. An angle lead greater than 180o may also be represented
as an angle lag of less that 180o . For all figures we have adopted the phase
lag convention   y x
Lissajous Figures

41. Linear Polarization ( = m)

42. Circular Polarization ( = /2)

43. Elliptical Polarization