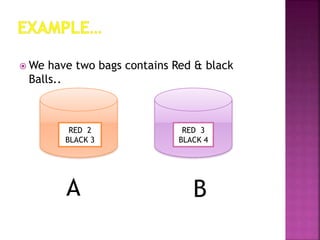
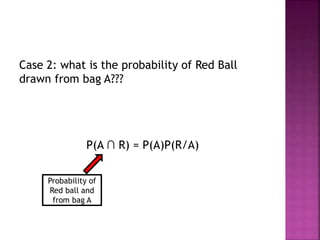
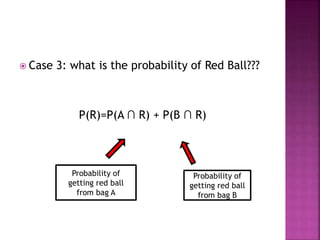
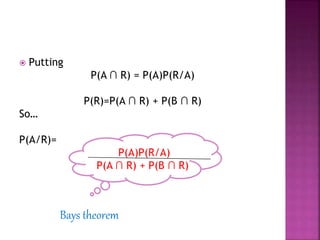
Bayes' theorem describes the probability of an event based on prior knowledge of conditions related to the event. For example, a person's age can make the probability of them having cancer more accurate than without knowing their age. Bayesian inference applies Bayes' theorem to statistical analysis by updating probabilities based on new evidence. The example problem calculates probabilities of drawing a red ball from two bags with different numbers of red and black balls using Bayes' theorem. It finds the probability of a red ball being from bag A given that a red ball was drawn is 2/5 divided by the total probability of drawing a red ball from either bag.

1. THROUGH ONE EXAMPLE………….
MADE BY:-
MAYANK
MULCHANDANI

2.  In probability theory and statistics, Bayes'
theorem (alternatively Bayes' law or Bayes'
rule) describes the probability of an event,
based on prior knowledge of conditions that
might be related to the event. For example,
if cancer is related to age, then, using
Bayes' theorem, a person's age can be used
to more accurately assess the probability
that they have cancer, compared to the
assessment of the probability of cancer
made without knowledge of the person's
age.

3. One of the many applications of Bayes'
theorem is Bayesian inference, a particular
approach to statistical inference. When
applied, the probabilities involved in Bayes'
theorem may have different probability
interpretations. With the Bayesian
probability interpretation the theorem
expresses how a subjective degree of belief
should rationally change to account for
availability of related evidence. Bayesian
inference is fundamental to Bayesian statistics.

4.  We have two bags contains Red & black
Balls..
A B
RED 2
BLACK 3
A
RED 3
BLACK 4

5. Case 1: what is the probability of get’s Red Ball
from bag A??? { bag A is already selected}
Should be written as…
P(R/A) = 2/5

6. Case 2: what is the probability of Red Ball
drawn from bag A???
P(A ∩ R) = P(A)P(R/A)
Probability of
Red ball and
from bag A

7.  Case 3: what is the probability of Red Ball???
P(R)=P(A ∩ R) + P(B ∩ R)
Probability of
getting red ball
from bag A
Probability of
getting red ball
from bag B

8.  Case 4: Given that red ball is drawn .what is
the probability that the Ball is from bag A ???
 P(A/R)=
P(A ∩ R)
P(A ∩ R) + P(B ∩ R)

9.  Putting
P(A ∩ R) = P(A)P(R/A)
P(R)=P(A ∩ R) + P(B ∩ R)
So…
P(A/R)=
P(A)P(R/A)
P(A ∩ R) + P(B ∩ R)
Bays theorem

10. Made by:-
MAYANK MULCHANDANI